[Algorithm] 정규식(Regular Expressions)

📕 목차

1. Regular Expressions (RE)
2. Nondeterministic Finite-state Automata (NFA)
3. NFA를 이용하여 문자열 인식
4. RE로부터 NFA 작성

1. Regular Expressions (RE)

📌 패턴 매칭 (Pattern Matching)

문자열 매칭: Text에서 하나의 pattern 문자열을 발견하는 것이 목적
패턴 매칭: 특정 조건을 만족하는 문자열의 집합 중에 한 가지라도 Text에 나타나는가?

예를 들어, 유전 공학의 DNA 염기 서열을 생각해보자.

사람의 유전자는 알파벳 A, C, T, G로 표현하며, GCG로 시작해서 CTG로 끝나며, 중간에 CGG나 AGG가 여러 번 나오는 패턴을 검색하려 한다.

text로 "GCGGCGTGTGTGCGAGAGAGTGGGTTTAAAGCTGGCGCGGAGGCGGCTGGCGCGG"가 들어왔을 때, RE는 이러한 패턴을 정의할 때 사용한다.

📌 Regular Expressions 정의

RE은 아래 중 하나이다.

Empty String
하나의 문자
괄호에 쌓인 RE
두 개 이상의 RE가 연결된 것
or 연산자(|)로 분리된 두 개 이상의 RE
closure 연산자(*)가 뒤에 붙은 RE

연산	순서	RE의 예	일치	불일치
연결	3	AABAAB	AABAAB	다른 모든 문자열
or	4	AA\|BAAB	AA BAAB	다른 모든 문자열
closure	2	AB*A	AA ABBBBBA	AB ABABA
괄호	1	A(A\|B)AAB	AAAAB ABAAB	다른 모든 문자열
괄호	1	(AB)*A	A ABABABABABA	AA ABBA

✒️ 편의성을 위해 추가된 연산자들

연산	RE의 예	일치	불일치
wildcard	.U.U.U.	CUMULUS JUGULUM	SUCCUBUS TUMULTUOUS
character class	[A-Za-z][a-z]*	word Capitalized	camelCase 4illegal
하나 이상	A(BC)+DE	ABCDE ABCBCDE	ADE BCDE
정확히 k개	[0-9]{5}-[0-9]{4}	08540-1321 19072-5541	111111111 166-54-111

[A-E]+는 (A|B|C|D|E)(A|B|C|D|E)*와 동일하다.

📌 정규 표현식 패턴

1️⃣ Character classes

문자 종류를 구분하는 데 사용한다.

정규식 패턴	설명	예시
\w	문자만 허용하는 정규 표현식	^\\w*$
\W	문자가 아닌 경우에만 허용하는 정규 표현식	^\\W*$
\d	숫자만 허용하는 정규 표현식	^\\d*$
\D	숫자가 아닌 경우에만 허용하는 정규 표현식	^\\D*$
\s	공백 문자, 탭만을 허용하는 정규 표현식	^\\s*$
\S	공백 문자, 탭이 아닌 경우에만 허용하는 정규 표현식	^\\S*$

참고로 `\d`라고만 쓰면 이스케이프 문자로 인식해서, 컴파일 실패가 발생한다.

그래서 `\\d`처럼 작성해야 함.

2️⃣ Assertions

행, 단어의 시작과 끝을 나타내는 경계를 표시하는 데 사용한다.

정규식 패턴	설명	예시
^	문장의 시작 (특정 문자열로 시작)	"^hello"
$	문장의 끝 (특정 문자열로 끝남)	"world$"

✒️ ^, $ 유무의 차이

개인적으로 이 내용이 조금 헷갈려서, 직접 실행해봤다.

public class RegularExpressions {
    public static void main(String[] args) {
        String[] testStrings = {"12345", "abc123", "123abc", "", "abc"};

        Pattern pattern1 = Pattern.compile("^\\d*$");
        Pattern pattern2 = Pattern.compile("\\d*");
        Pattern pattern3 = Pattern.compile("^\\d*");
        Pattern pattern4 = Pattern.compile("\\d$");

        System.out.println("Pattern 1: ^\\d*$");
        for (String s : testStrings) {
            Matcher matcher1 = pattern1.matcher(s);
            System.out.println("String: " + s + " -> " + matcher1.matches());
        }

        System.out.println("\nPattern 2: \\d*");
        for (String s : testStrings) {
            Matcher matcher2 = pattern2.matcher(s);
            System.out.println("String: " + s + " -> " + matcher2.find());
        }

        System.out.println("\nPattern 3: ^\\d*");
        for (String s : testStrings) {
            Matcher matcher3 = pattern3.matcher(s);
            System.out.println("String: " + s + " -> " + matcher3.find());
        }

        System.out.println("\nPattern 4: \\d$");
        for (String s : testStrings) {
            Matcher matcher4 = pattern4.matcher(s);
            System.out.println("String: " + s + " -> " + matcher4.find());
        }
    }
}

문자열	*^\d$**	\d*	^\d*	\d$
12345	✅	✅	✅	✅
abc123	❌	✅	✅	✅
123abc	❌	✅	✅	❌
(빈 문자열)	✅	✅	✅	❌
abc	❌	✅	✅	❌

* 카드의 존재 때문에 `\d*`는 숫자가 있거나, 없는 경우를 모두 허용하므로 all true.

`^\d*` 또한 숫자로 시작하거나, 숫자가 0개 있어도 되므로 all true.

하지만 `\d$`는 문자열이 반드시 숫자로 끝나야만 하며, `^\d*$`는 문자열이 오직 숫자로만 이루어져 있거나 빈 문자열이어야 한다.

3️⃣ Quantifiers

일치시킬 문자 또는 표현식의 수를 의미한다.

정규식 패턴	설명	예시
?	없거나 있거나 (zero or one)	a?b → "b", "ab"
*	없거나 있거나 많거나 (zero or more)	a*b → "b", "ab", "aaab"
+	하나 또는 많이 (one or more)	a+b → "ab", "aaab"
{n}	n개가 있는	a{3} → "aaa"
{min,}	최소	a{2,} → "aa", "aaa", ...
{min, max}	최소/최대 (최대가 5면 5개까지)	a{2, 5} → "aa", "aaa", ..., "aaaaa"

4️⃣ Group and Range

정규식 문법을 그룹화하거나 범위를 지정할 수 있다.

정규식 패턴	설명	예시
()	그룹	(abc)
[]	문자셋, 괄호 안의 어떤 문자든	[abc]
[^]	부정 문자셋, 괄호 안의 어떤 문자가 아니면	[^abc]
(?:)	찾지만 기억하지 않음.	(?:abc) → "abc" (캡처되지 않음)
(?=)	=앞 문자를 기준으로 전방 탐색	(?=abc) → "1abc2abc3"에서 '1', '2'
(?<=)	=뒤 문자를 기준으로 후방 탐	(?<=abc) → "abc1abc2abc3"에서 '1', '2', '3'

🤔 (?:), (?=), (?<=) ????

처음보면 이게 대체 뭔 소린가 싶겠지만, 자바에선 패턴에 그룹(`()`)으로 지정하면, 이후 그룹의 개수 카운트 등의 유용한 메서드들을 제공해준다.
여기서 캡처되지 않는다는 것은 만약 "(?:abc)"로 매칭된 결과를 얻었지만, 이후 그룹 카운트를 확인해도 카운팅되지 않았으므로 0이 반환된다.

📌 java.util.regex.Pattern

문자열을 정규표현식 패턴 객체로 변환해주는 클래스

컴파일된 정규식은 Matcher 클래스에서 사용한다.

import java.util.regex.*;

public static void main(String[] args) {
    String text = "1234567890";
    String regex = "^[0-9]*$";
    
    Pattern pattern = Pattern.compile(regex);
    Matcher matcher = pattern.matcher(text);
    
    System.out.println(m.matches());
}

메서드	설명
compile(String regex)	정규 표현식의 패턴 작성
matches(String regex, CharSequence input)	정규 표현식의 패턴과 문자열이 일치하는지 검사 일부 문자열이 아닌, 전체 문자열과 완벽히 일치해야 한다.
asPredicate()	문자열을 일치시키는 데 사용할 수 있는 술어를 작성
pattern()	컴파일된 정규표현식을 String 형태로 반환
split(CharSequence input)	문자열을 주어진 인자값 CharSequence 패턴에 따라 분리

[Effective-Java] Chapter2 #6. 불필요한 객체 생성을 피하라

기존 객체를 재사용해야 한다면 새로운 객체를 만들지 마라. 📌 기존의 인스턴스를 재사용하자 String 객체를 예시로 들어보자. String s = new String("Java"); String을 new로 생성하면 매번 새로운 객체를

jaeseo0519.tistory.com

참고로 단순히 코테 목적이나 공부용이 아닌, 진짜 개발할 때 Pattern을 컴파일할 거라면 캐싱을 해두어라.

여기서 말하는 유한 상태 머신에 대한 내용은 아래에서 다룰 것이다.

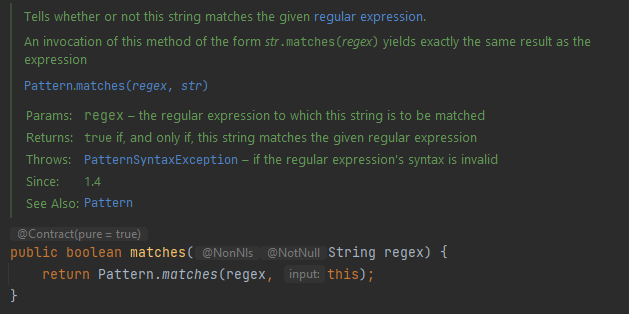
String 타입의 인스턴스에서 제공하는 .matches() 또한 내부적으로 Pattern 인스턴스를 생성한다.

📌 java.util.reges.Matcher

대상 문자열에 대한 패턴을 해석하고, 주어진 패턴과 일치하는 지 판별한 후 반환된 필터링된 결과값을 갖는다.

메서드	설명
find()	대상 문자열과 패턴이 일치하는 경우 true를 반환하고, 그 위치로 이동한다. (여러 개가 매칭되는 경우 반복 실행했을 때, 일치하는 부분 다음부터 이어서 매칭된다.)
find(int start)	start 위치 이후부터 매칭 검색
start()	매칭되는 문자열의 시작 위치 반환
start(int group)	지정된 그룹이 매칭되는 시작 위치 반환
end()	매칭되는 문자열 끝 위치의 다음 문자 위치 반환
end(int group)	지정된 그룹이 매칭되는 끝 위치의 다음 문자 위치 반환
group()	매칭된 부분을 반환
group(int group)	매칭된 부분 중 group번 그루핑 매칭 부분 반환
groupCount()	패턴 내 그룹핑(`()`)한 패턴의 전체 개수 반환
matches()	패턴이 전체 문자열과 일치할 경우 true 반환

📝 예제

프로그래머스

코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.

programmers.co.kr

위 문제는 조건문, 반복문으로만 해결하려면 코드가 엄청 장황해지는데, 정규식을 쓰면 매우 간단하게 풀 수 있다.

정규식이 이해 안 가면 그냥 위 문제를 풀어보면 된다.

입력 형식은 언제나 "점수|보너스|[옵션]"이므로, 다음과 같이 표현할 수 있다. (물론 더 많은 방법으로 표현 가능함)

점수는 0~10 사이의 정수: "[0-9]+"
보너스는 SDT 중 하나이다. : "[SDT]"
옵션은 *이나 # 중 하나이며, 없을 수도 있다. : "[*#]?"

물론 저 위의 표현식을 그대로 합칠 수도 있지만, "(점수|보너스|[옵션])(점수|보너스|[옵션])(점수|보너스|[옵션])" 매칭 검사를 하고 각각에 대해 또 "(점수|보너스|[옵션])" 매칭 검사를 하는 건 좀 귀찮다.

그래서 처음부터 "([0-9]+)([SDT])([*#]?)"라고 해주는 게 편하다.

private static final String REGX = "([0-9]+)([SDT])([*#]?)";
private static final Pattern pattern = Pattern.compile(REGX + REGX + REGX);

그런 다음 그룹을 확인할 때 한 번에 3개씩 읽으면 된다.

for (int i=1; i<matcher.groupCount(); i+=3) {
    int point = Integer.parseInt(matcher.group(i));
    int bonus = darts.get(matcher.group(i+1));
    int option = (!matcher.group(i+2).isBlank()) ? options.get(matcher.group(i+2)) : 1;
    
    ...
}

참고로 매칭되는 결과가 없으면 null이 반환된다길래, 굳게 믿고 `matcher.group(i+2) == null`로 했다가 틀렸다.

띠옹?? 왜지? 매칭되는 결과 없으면 null이라며?

근데 생각해보니까 "[*#]?"면 "* 혹은 # 혹은 없는 경우"를 의미한다.

그니까 ""도 패턴 매칭이 됐다고 판단해서 결과가 null이 아니라 빈 문자열이 반환된다 ㅋㅋㅋㅋ

2. Nondeterministic Finite-state Automata (NFA)

📌 RE와 DFA(Deterministic Finite-state Automata)

RE: 문자열의 집합을 표현하는 효율적인 방법
DFA: 문자열이 주어진 집합에 포함되는지 인식하는 기계

📌 Kleen의 이론

💡 RE와 DFA는 서로 표현력이 같다.

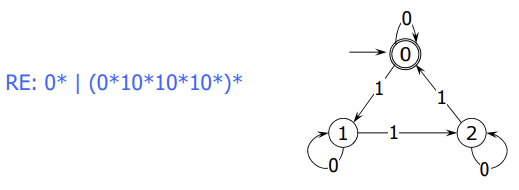
DFA가 주어지면, 그 DFA가 인식하는 문자열의 집합을 표현하는 RE가 존재한다.
역으로 RE가 주어지면, 동일한 문자열의 집합을 인식하는 DFA가 존재한다.

📌 패턴 매칭 구현 방법

DFA를 사용하면?
- RE로부터 DFA를 작성
- 입력 text를 이용해 DFA 상태를 이동 후, 최종 상태에서 종료하게 되면 해당 text를 accept
문제점: RE의 or 연산에 의해 DFA는 상태의 수가 지수함수적으로 증가할 수 있다.
- OR 연산이 많아지면, 각 선택지는 독립적인 상태로 표현되어야 한다.
- 따라서, OR 연산이 N개면, 각 연산이 2개의 선택지를 가질 때 상태 수는 $2^{N}$이 된다.
해결법: 비결정적 유한 상태 머신(NFA; Nondeterministic Finite-state Automata)를 사용하면 된다.
- 각 상태에서 특정 입력 기호에 대해 전이할 수 있는 상태가 단 하나인 DFA와 달리 여러 개의 전이 상태가 존재할 수 있다.

특성	DFA	NFA
전이 결정성	각 상태에서 하나의 고유한 다음 상태	각 상태에서 여러 개의 다음 상태 가능
전이 함수	δ : Q * ∑ → Q (Q는 상태 집합, ∑ 는 입력 알파벳)	δ : Q * ∑ → $2^{Q}$
상태 수락	단 하나의 경로가 수락 상태에 도달해야 함	여러 경로 중 하나라도 수락 상태에 도달하면 됨
상태 전이	명시적 상태 전이, 고유한 다음 상태	여러 전이 가능, ε-전이 가능
복잡성	일반적으로 더 많은 상태 필요	일반적으로 적은 상태로 표현 가능
구현	구현이 간단하고 결정적임	구현이 더 복잡하고 비결정적임

📌 NFA

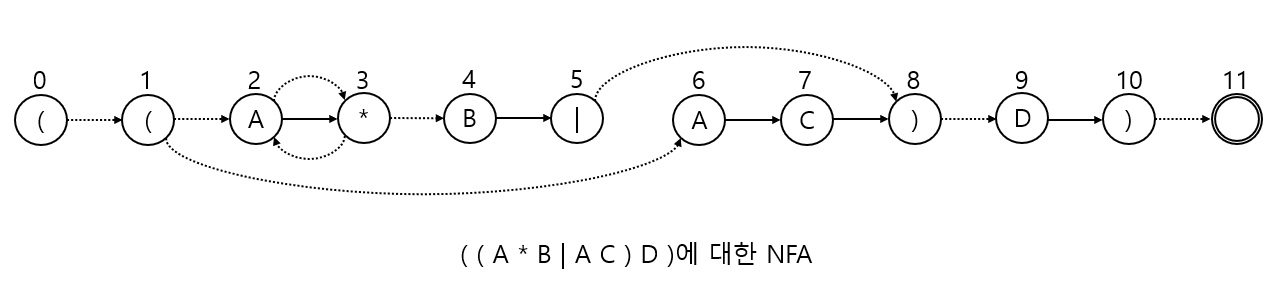
RE의 각 문자마다 하나의 상태를 가짐 (시작 = 0, 최종 M)
ε-이동은 점선으로 표시하고 상태는 이동하되, 텍스트 스캔은 하지 않음 (가도 되고, 안 가도 되는 엣지)
실선은 상태 이동 후, 다음 문자를 스캔하여 텍스트 매치
모든 문자를 스캔한 후, 하나의 이동이라도 M에 도착하면 일치

즉, NFA에서 text 인식은 ε-이동으로 인해 여러 개의 상태 이동 결과가 존재하는 Nondeterministic한 방법이다.

📌 NFA를 이용한 문자열 인식의 예

검색 문자열이 "AABD"라고 가정
초기 상태는 ε-이동에 의해 {0, 1, 2, 3, 4, 6}
매칭 순서
1. A 입력: {0, 1, 2, 3, 4, 6} → {3, 2, 4, 7}
2. A입력: {3, 2, 4, 7} → {3, 2, 4}
3. B입력: {3, 2, 4} → {5, 8, 9}
4. D입력: {5, 8, 9} → {10, 11}

3. NFA를 이용하여 문자열 인식

📌 아이디어

char 배열 re[]로 상태를 표현
- re[0]: 초기 상태
- re[M]: 최종 상태
- re[i]: i번 째 RE 문자
- 입력 테스트 == r[i]일 경우, i에서 i+1로 match transition
ε-이동: Digraph G(0 → 1, 1 → 2, 1 → 6, ⋯)로 표현
문자열 인식 방법
1. 0부터 DFS 수행 → 도착 가능한 상태 저장
2. 각 상태에서 match transition 후, 이동한 상태에 대해 다시 DFS 수행
3. Text의 모든 문자에 대해 위 과정 반복

📌 NFA 문자 인식 코드 작성

public boolean recognize(String txt) {
    List<Integer> pc = new LinkedList<>();
    DirectedDfs dfs = new DirectedDfs(G, 0); // 0부터 DFS 수행
        
    for (int v = 0; v < G.V(); ++v) {
        if (dfs.marked(v)) { // dfs에서 방문한 모든 노드를 리스트에 추가
            pc.add(v);
        }
    }
        
    List<Integer> match = new LinkedList<>();
    for (int i=0; i<txt.length(); ++i) {
        match.clear();
            
        for (int v : pc) { // 리스트의 노드에 대해 match transition의 결과 노드 저장
            if (v < M && (re[v] == txt.charAt(i) || re[v] == '.')) {
                match.add(v+1);
            }
        }
            
        pc.clear();
        dfs = new DirectedDfs(G, match); // match transition의 결과 노드에 대해 ε-이동 수행
            
        for (int v = 0; v < G.V(); ++v) {
            if (dfs.marked(v)) {
                pc.add(v); // dfs에서 방문한 모든 노드를 리스트에 추가
            }
        }
    }
        
    for (int v : pc) {
        if (v == M) return true; // 마지막 문자까지 매칭한 후, accept 상태에 도달하면 true 반환
    }
        
    return false;
}

✒️ DirectedDfs

예시에 해당 코드가 없어서 대충 흐름 보고 만들어봤는데, 제대로 구현했는지 검증은 하지 않았다.

/**
 * DirectedDfs 클래스는 유향 그래프에서 깊이 우선 탐색을 수행하는 클래스이다.
 * 생성자에서 유향 그래프 G와 시작 정점 s를 입력으로 받아 깊이 우선 탐색을 수행한다.
 */
class DirectedDfs {
    private final boolean[] marked;

    public DirectedDfs(Digraph G, int s) {
        marked = new boolean[G.V()];
        dfs(G, s);
    }

    public DirectedDfs(Digraph G, Iterable<Integer> sources) {
        marked = new boolean[G.V()];
        for (int s : sources) {
            if (!marked[s]) {
                dfs(G, s);
            }
        }
    }

    private void dfs(Digraph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    public boolean marked(int v) {
        return marked[v];
    }
}

4. RE로부터 NFA 작성

📌 작성 단계

1️⃣ RE의 각 문자에 대한 상태와 최종 상태 생성

2️⃣ 알파벳에 해당하는 문자의 상태에서 다음 상태로 match-transition 추가

3️⃣ 괄호에서 다음 상태로 ε-이동 엣지 추가

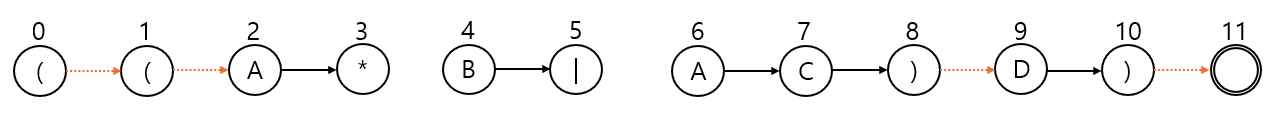
4️⃣ * 연산자에 대해 ε-이동 엣지 추가

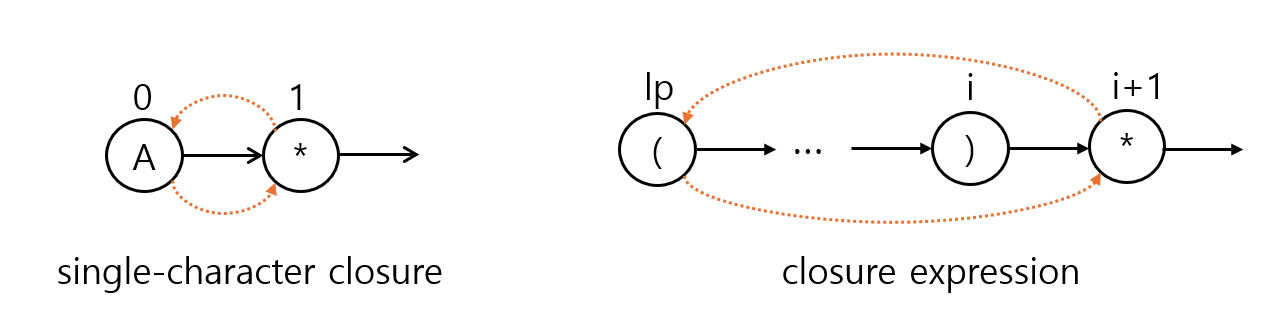
*는 zero or more 상태이므로, 앞에 문자가 있는지 괄호가 있는지에 따라 양방향 ε-이동 엣지를 추가해주어야 한다.

5️⃣ | 연산자마다 두 개의 ε-이동 엣지 추가

or expression, 1, 2번 상태 이동할 때 실선인데 실수로 점선으로 표현했다.

or 연산자(|) 또한 그렇게 어렵지 않다.

괄호가 시작할 때 | 연산자 이후의 상태로 가는 ε-이동 엣지를 추가하고, | 연산자가 닫힌 괄호로 이동하는 ε-이동 엣지를 추가한다.

참고로 | 연산자 상태에서 바로 다음 상태로 가는 엣지는 없어야 한다. (그게 or 연산이니까...)

📌 구현 방안

goal: ε-이동 엣지를 추가하는 프로그램
어려운 점
- * 연산과 | 연산을 위해 '('를 기억해야 한다.
- ')'를 반날 때, | 상태에서 edge를 추가해줘야 하므로 '|'도 기억해야 한다.
해결 방법 : Stack을 이용
1. RE의 왼쪽 문자부터 차례로 스캔한다.
2. '(' 문자를 만나면, 스택에 '('의 상태 번호를 추가한다.
3. '|' 문자를 만나면, 스택에 '|'의 상태 번호를 추가한다.
4. ')' 문자를 만나면, 스택에서 '('와 그 위에 있던 '|'를 삭제한 후, * 연산과 | 연산을 위한 ε-이동 엣지를 추가한다.

public class NFA {
    private final char[] re; // 정규 표현식
    private final int M; // 정규 표현식의 길이
    private final Digraph G; // ε-이동을 나타내는 유향 그래프

    public NFA(String regexp) {
        re = regexp.toCharArray(); // 정규 표현식을 문자 배열로 변환
        M = re.length; // 정규 표현식의 길이

        ArrayDeque<Integer> ops = new ArrayDeque<>();
        G = new Digraph(M+1); // 정규 표현식의 길이 + 1의 크기를 갖는 유향 그래프 생성

        for (int i=0; i<M; ++i) {
            int lp = i;

            if (re[i] == '(' || re[i] == '|') {
                ops.push(i);
            } else if (re[i] == ')') { // ( ) 사이에 '|'가 기껏해야 하나만 저장된다고 가정
                int or = ops.pop();

                if (re[or] == '|') {
                    lp = ops.pop();
                    G.addEdge(lp, or+1);
                    G.addEdge(or, i);
                } else {
                    lp = or;
                }
            }

            if (i < M-1 && re[i+1] == '*') {
                G.addEdge(lp, i+1);
                G.addEdge(i+1, lp);
            }

            if (re[i] == '(' || re[i] == '*' || re[i] == ')') {
                G.addEdge(i, i+1);
            }
        }
    }
 }

✒️ Digraph

이것도 그냥 혼자서 대충 만들어본 유향 그래프 클래스

/**
 * Digraph 클래스는 유향 그래프를 나타내는 클래스이다.
 * 생성자에서 정점의 개수 V를 입력으로 받아 인접 리스트를 초기화한다.
 * 정점의 개수 V와 간선의 개수 E, 인접 리스트 adj를 저장한다.
 */
class Digraph {
    private final int V; // 정점의 개수
    private int E; // 간선의 개수
    private final List<List<Integer>> adj; // 인접 리스트

    public Digraph(int V) {
        this.V = V;
        this.E = 0;
        adj = new LinkedList<>();
        for (int v=0; v<V; ++v) {
            adj.add(new LinkedList<>());
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    public void addEdge(int v, int w) {
        adj.get(v).add(w);
        E++;
    }

    public Iterable<Integer> adj(int v) {
        return adj.get(v);
    }
}

🟢 실행 결과

public static void main(String[] args) {
    NFA nfa = new NFA("((A*B|AC)D)");
    System.out.println(nfa.recognize("AABD")); // true
    System.out.println(nfa.recognize("ACD")); // true
    System.out.println(nfa.recognize("BD")); // true
    System.out.println(nfa.recognize("AABACD")); // false
    System.out.println(nfa.recognize("ACBD")); // false
}