📕 목차
1. 자바의 String 사전 지식
2. LSD(Least Significant Digit)
3. MSD(Most Significant Digit)
4. Three-way String Quicksort
1. 자바의 String 사전 지식
• char 데이터 타입 (feat. Character)
• String 데이터 타입
• StringBuilder
• 두 개의 문자열 비교
• Alphabet
• 문자열 정렬 알고리즘 필요성
📌 char 데이터 타입 (feat. Character)
C언어를 공부할 때는 char 타입이 8-bit(1byte)였는데, 자바에서는 16-bit(2byte)의 크기를 갖는다.
이는 제공하는 문자 체계가 다르기 때문이다.
- C: 7-bit의 ASCII 코드 지원
- Java: 16-bit의 Unicode 지원
🟡 Character
자바에서 char 기본 타입의 래퍼 클래스인 Character가 존재한다.

그런데 대부분 정적 메서드라서, 인스턴스로 활용할 일은 거의 없고 Util 같은 느낌으로 쓰게 된다.
📌 String 데이터 타입


String 클래스 자체도 final 키워드를 가지지만, 내부 byte[] 또한 final이다.
즉, 자바의 String은 한 번 생성되면 불변(Immutable)하다.
| 연산 | 문자 배열 | Java String | 실행 시간 |
| 선언 | char[] c | String s | |
| 길이 | c.length; | s.length(); | 1 |
| 인덱싱 | a[index]; | s.charAt(index); | 1 |
| 병합 | s + t | N + M | |
| 변환 | c = s.toCharArray();; | s = new String(c); |
📌 StringBuilder
[Effective-Java] Chapter9 #63. 문자열 연결은 느리니 주의하라
이건 자바로 코테 쳐봤으면 누구나 알 법한 이야기. 📌 String 문자열 연결 방식 public String statement() { String result = ""; for (int i = 0; i < numItems(); i++) result += lineForItem(i); return result; } 한 줄짜치 출력값
jaeseo0519.tistory.com
일반적으로 자바의 문자열을 + 연산자를 사용해 더하려고 하면 상당히 느리다.
public class StringPerformanceMeasurement {
public static void main(String[] args) {
// + 연산자 사용 시
long startTime = System.currentTimeMillis();
String str = "";
for (int i = 0; i < 10000; i++) {
str += "x";
}
long endTime = System.currentTimeMillis();
System.out.println("String: " + (endTime - startTime) + "ms");
// StringBuilder 사용 시
startTime = System.currentTimeMillis();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 10000; i++) {
sb.append("x");
}
endTime = System.currentTimeMillis();
System.out.println("StringBuilder: " + (endTime - startTime) + "ms");
}
}
String은 불변하므로 더하기 연산 과정에서 기존 문자열과 새로 연결할 문자열을 모두 복사해야 하므로 시간 복잡도가
또한 중간에 발생한 무수히 많은 문자열이 생성되었다가 가비지 컬렉션에 의해 회수된다.
[Effective-Java] Chapter4 #17. 변경 가능성을 최소화하라 : 불변 클래스
불변 클래스란 그 인스턴스 내부 값을 수정할 수 없는 클래스를 말한다. 불변 인스턴스에 간직된 정보는 객체가 파괴되는 순간까지 절대 달라지지 않는다. 자바 플랫폼 라이브러리의 String, 기본
jaeseo0519.tistory.com
StringBuilder는 이러한 불변 클래스인 String의 가변 동반 클래스로써, 내부에 mutable char[] 배열을 사용해 더하기 연산자 보다 훨씬 빠른 성능을 낼 수 있다.
append() 를 사용한 문자열 연결의 시간 복잡도는
| 메서드 | 설명 |
| .append() | 문자열을 추가한다. |
| .insert(int offset, String str) | offset 위치에 str을 추가한다. |
| .replace(int start, int end, String str) | start와 end-1 사이의 문자열을 str로 대체한다. |
| .substring(int start, int end) | start와 end-1 사이의 문자열을 반환한다. end가 없으면 start부터 끝까지 반환한다. |
| .deleteCharAt(int index) | index에 위치한 문자를 삭제한다. |
| .delete(int start, int end) | start부터 end-1 까지의 문자열을 삭제한다. |
| .toString() | String으로 변환한다. |
| .reverse() | 문자를 뒤집는다. |
| .setCharAt(int index, String s) | index 위치의 문자를 s로 변경한다. |
| .setLength(int len) | 문자열 길이를 조정한다. 현재 문자열보다 길게 조정하면 공백으로 채워진다. 현재 문자열보다 짧게 조정하면 나머지 문자는 삭제된다. |
| .trimToSize() | 내부적으로 문자열을 저장한 char[] 배열 사이즈를 현재 문자열 길이와 동일하게 조정한다. 문자열 뒷부분의 공백을 제거해준다고 보면 된다. |
🟡 append()

StringBuilder의 문자열을 추가해주는 append 메서드는 어미의 마음으로 온갖 타입을 다 받아준다.
그냥 내부에서 String.valueOf() 나 toString 메서드 호출해주겠거니 싶었는데
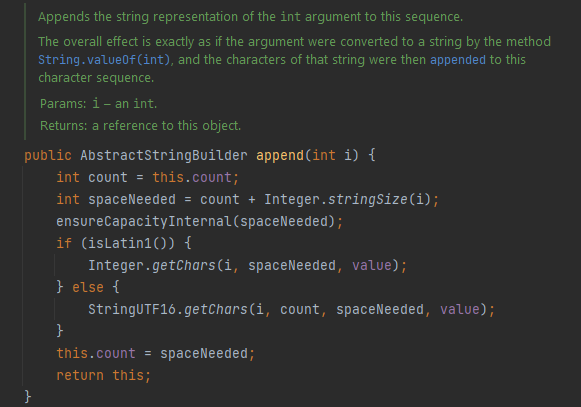
AbstractStringBuilder를 살펴보면 온갖 괴랄한 코드가 나와서 일단 도망쳤다.
나중에 뜯어볼게 생겨서 신난다.
✒️ JDK 9 이후의 String 더하기 연산자
String이 value를 char[]가 아닌 byte[]로 취급하면서 내부 구현이 바뀌었다.
따라서 문자열의 크기가 작고, 반복 횟수가 그리 크지 않다면(1000회 미만) 오히려 StringBuilder보다 효율적인 방식으로 문자열을 연결하기도 한다. (StringBuilder 인스턴스를 생성하지도 않으므로 메모리 사용량도 줄일 수 있다.)
📌 두 개의 문자열 비교
| p | r | e | f | e | t | c | h |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | r | e | f | i | x | e | s |
길이가 N인 두 개의 문자열을 비교하기 위해서 최악의 경우 O(N) 실행 시간이 필요하다.
상수 시간이라 괜찮겠지라고 생각하기엔, 문자열은 정말 방대한 양을 담고 있는 경우도 존재한다.
따라서 String을 위한 전용 정렬 알고리즘이 필요하다.
📌 문자열 정렬 알고리즘 필요성
| 알고리즘 | 시간 복잡도 | 공간 복잡도 | Stable | 키 연산 |
| 삽입정렬(insertion) | N^2 | 1 | ✅ | compareTo() |
| 합병정렬(merge sort) | N logN | N | ✅ | compareTo() |
| 퀵정렬(quick sort) | N logN | logN | compareTo() | |
| 힙정렬(heap sort) | N logN | 1 | compareTo() |
기존의 정렬 알고리즘을 사용하기엔 길이가 N인 문자열에 대해 compareTo() 연산은 N logN번 호출되어야 한다.
문자 비교를 줄이는 캐릭터 비교연산 알고리즘이 필요한 이유
2. LSD(Least Significant Digit)
• LSD 정렬
• 성능
📌 LST 정렬

public class LSD {
private static void sort(String[] a, int W) { // 모든 문자 길이가 W
int N = a.length;
int R = 256; // 기수 = R (ASCII)
String[] aux = new String[N];
for (int d = W-1; d >= 0; d--) { // d: 문자열의 d번째 문자, LSD이므로 뒤에서부터
int[] count = new int[R];
for (String s : a) {
count[s.charAt(d)]++; // d번째 문자의 빈도수 계산
}
for (int r = 1; r < R; r++) {
count[r] += count[r-1]; // 누적 빈도수 계산
}
for (int i = N - 1; i >= 0; i--) {
aux[--count[a[i].charAt(d)]] = a[i]; // 뒤 문자열부터 뒤에서 저장 : stable
}
for (int i = 0; i < N; i++) {
a[i] = aux[i]; // 정렬된 배열로 복사
}
}
}- 모든 문자열의 길이가 동일할 때 사용할 수 있다. (고정 길이)
- 기수 정렬을 사용해 오른쪽에서 왼쪽으로 문자들을 비교한다.
💡 기수 정렬(Radix Sort)
- 나보다 작은 값만 파악해서 해당 위치로 이동하는 방법
- 키 값이 0 ~ K-1 사이의 정수인 경우에만 적용할 수 있다.
- 3개의 배열이 필요
- 입력 배열 A[n], 임시 배열 C[K], 결과 배열 B[n]
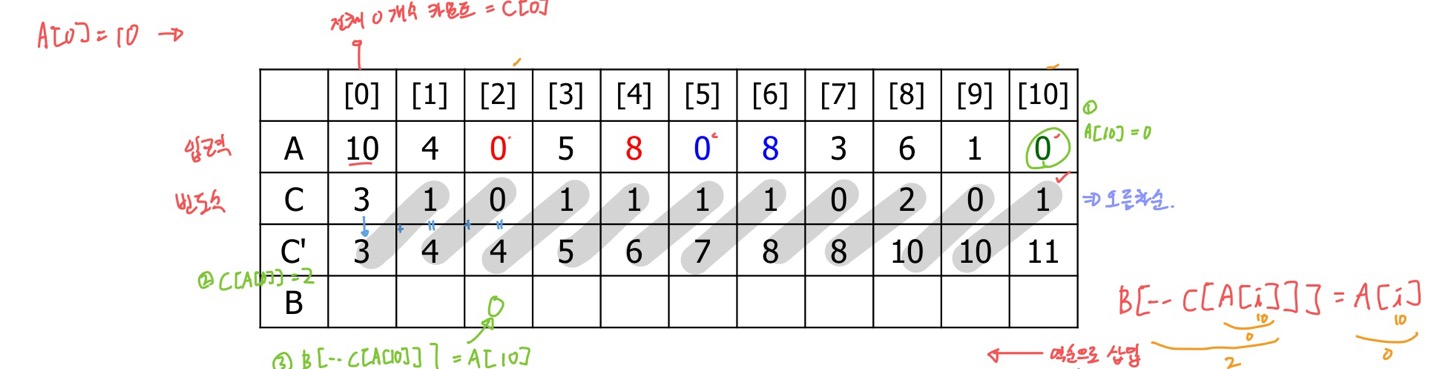
- A에 나오는 모든 값들에 대해서 빈도수를 C에 계산한다.
- A[0]에서 10이라는 수가 있으므로, C[10]을 1 증가시킨다.
- 역순으로 삽입하는 이유는 동일값에 대한 순서를 보장하기 위함이며, 따라서 LSD는 stable sort라고 볼 수 있다.
📌 성능
| 알고리즘 | 시간 복잡도 | 공간 복잡도 | Stable | 키 연산 |
| 삽입정렬(insertion) | N^2 | 1 | ✅ | compareTo() |
| 합병정렬(merge sort) | N logN | N | ✅ | compareTo() |
| 퀵정렬(quick sort) | N logN | logN | compareTo() | |
| 힙정렬(heap sort) | N logN | 1 | compareTo() | |
| LSD 정렬 | W(N+R) | N+R | ✅ | charAt() |
- 모든 문자열의 길이가 같고, N이 충분히 크다면 퀵 정렬보다 빠르다. (W, R을 상수로 치면, 사실 상 O(N)으로 취급)
- 하지만 일반적으로 비교하는 문자열의 길이가 같은 경우가 드물다.
- 자리수가 무제한에 가깝거나, 문자열이 모두 다른 경우 퀵 정렬보다 느릴 수 있다.
3. MSD(Most Significant Digit)
• MSD 정렬
• 가변 길이 문자열에 대한 처리
• 성능
📌 MSD 정렬
public class MSD {
private static final int M = 15; // 삽입 정렬을 위한 임계값
private static final int R = 256; // 기수
private static String[] aux = {};
public static void sort(String[] a) {
int N = a.length;
aux = new String[N];
sort(a, 0, N-1, 0);
}
private static void sort(String[] a, int lo, int hi, int d) {
if (hi <= lo + M) { // cutoff : M = 15, 삽입 정렬이 더 빠름
Insertion.sort(a, lo, hi, d);
return;
}
int[] count = new int[R+2]; // R: 문자열의 길이, R+2: 앞에서 저장 & EOS 공간 필요
for (int i = lo; i <= hi; i++) {
count[charAt(a[i], d) + 2]++; // count[1]: EOS(End of String) 공간
}
for (int r = 0; r < R+1; r++) {
count[r+1] += count[r];
}
for (int i = lo; i <= hi; i++) {
aux[count[charAt(a[i], d) + 1]++] = a[i];
}
for (int i = lo; i <= hi; i++) {
a[i] = aux[i - lo]; // aux는 전역 배열로 한 번만 할당
}
for (int r = 0; r < R; r++) {
sort(a, lo + count[r], lo + count[r+1] - 1, d+1); // R개의 부분 배열에 대해 정렬
}
}
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}
}count 배열 값 변화
| 루프 횟수 | 0 | 1 | 2 | 3 | ⋯ |
| 1 | 0 | -1의 수 | a의 수 | b의 수 | |
| 2 | -1의 위치 | a의 위치 | b의 위치 | ||
| 3 | -1의 수 | -1 ~ a의 수 | -1 ~ b의 수 |
- 모든 문자의 길이가 달라도 사용할 수 있다.
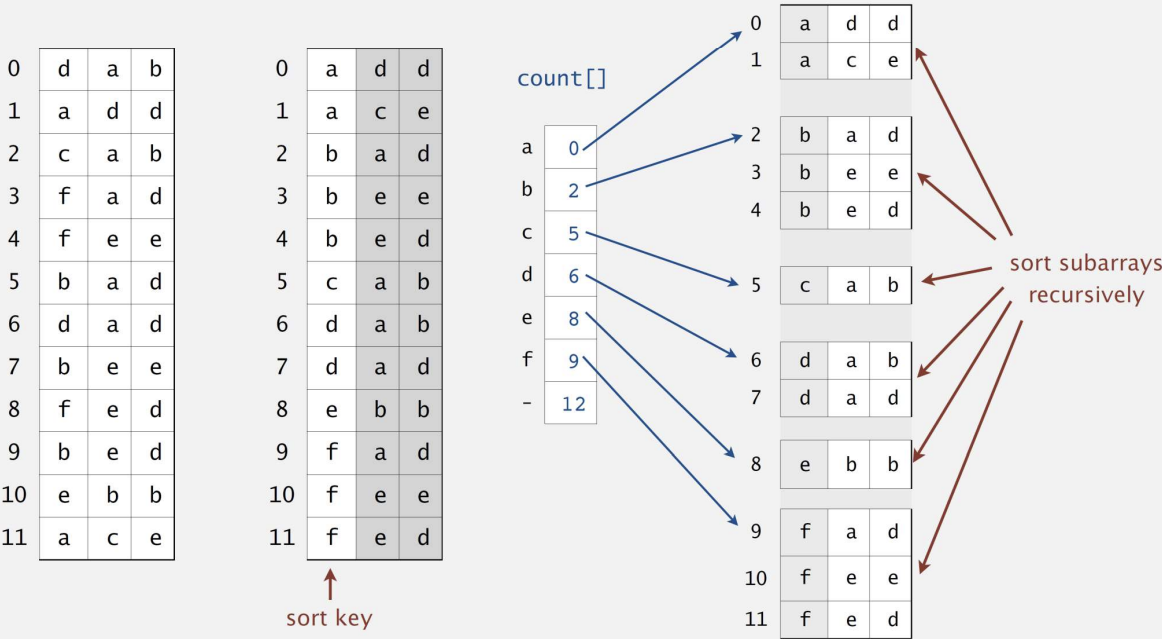
- 첫 번째 문자를 기준으로 R개의 분할을 생성한다. (기수 정렬 기반)
- 각 분할에 대해 다시 다음 문자를 기준으로 수 정렬을 수행한다.
🟡 동작 과정
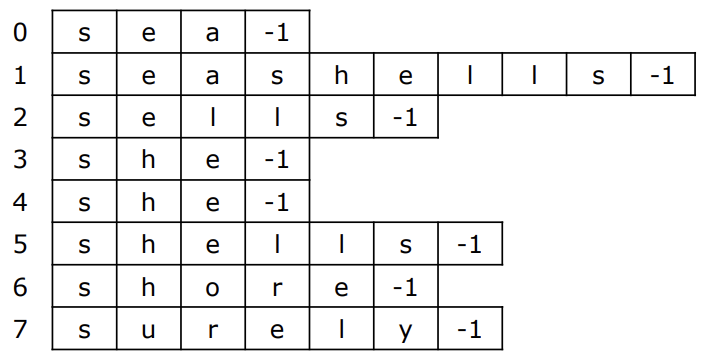
input 값이 다음과 같다고 하자.
String[] a = {"she", "sells", "seashells", "by", "the", "sea", "shore", "the", "shells", "she", "sells", "are", "surely", "seashells"};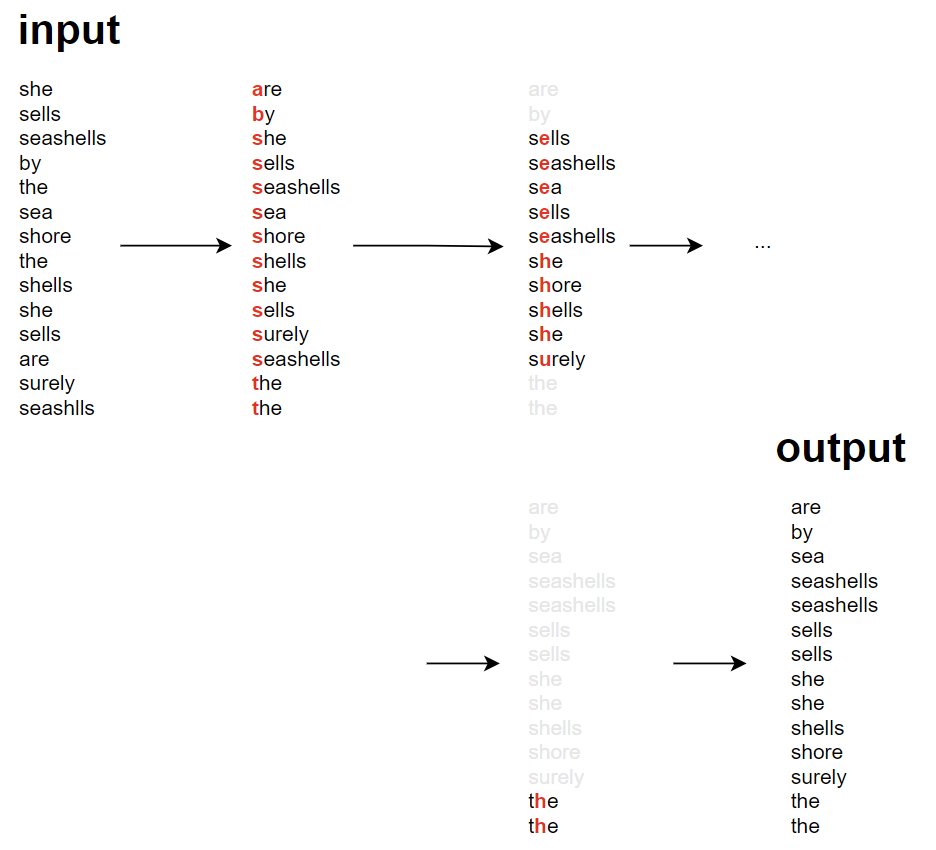
- 가장 첫 번째 문자를 기준으로 문자를 정렬한다. (첫 번째 문자가 동일한 단어끼리 그룹이 형성됨)
- 문자가 같았던 그룹끼리 다시 정렬을 수행하도록 재귀를 호출한다.
처음에 이거 보는데 이해 안 서 머리 아팠는데, 이해하고 나니 별 거 아니었던 황당한 알고리즘
📌 가변 길이 문자열에 대한 처리
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}count 배열에서 왜 chatAt()이라는 함수를 따로 정의했냐면, 문자열의 길이가 모두 다를 수 있기 때문에 EOS(End of String)으로 -1(가장 작은 문자)이라는 값을 넣어주기 위함이었다.
C언어로 구현하면 `\0`이 들어가므로 추가 작업이 필요없는데, 자바라서 필요한 것
📌 성능
- 문자열이 모두 다르다면 선형 이하의 시간을 갖는다.
- 중복이 존재하는 경우 거의 선형 시간에 가깝다.
- 모든 문자열이 같은 경우 선형 시간이 소요되어 가장 최악의 케이스가 된다.
| 알고리즘 | 시간 복잡도 | 공간 복잡도 | Stable | 키 연산 |
| 삽입정렬(insertion) | N^2 | 1 | ✅ | compareTo() |
| 합병정렬(merge sort) | N logN | N | ✅ | compareTo() |
| 퀵정렬(quick sort) | N logN | logN | compareTo() | |
| 힙정렬(heap sort) | N logN | 1 | compareTo() | |
| LSD 정렬 | W(N+R) | N+R | ✅ | charAt() |
| MSD 정렬 | 최악: W(N+R) 평균: N log_R(N) |
N + DR (D: 함수 호출 수) |
✅ | charAt() |
4. Three-way String Quicksort
• Three-way String QuickSort
• MSD 정렬과 비교
• 성능
📌 Three-way String QuickSort
public class ThreeWayStringQuickSort {
public static void sort(String[] a) {
sort(a, 0, a.length - 1, 0);
}
private static void sort(String[] a, int lo, int hi, int d) {
if (hi <= lo) {
return;
}
int lt = lo, gt = hi;
int v = charAt(a[lo], d);
int i = lo + 1;
while (i <= gt) {
int t = charAt(a[i], d);
if (t < v) {
exch(a, lt++, i++);
} else if (t > v) {
exch(a, i, gt--);
} else {
i++;
}
}
sort(a, lo, lt-1, d);
if (v >= 0) {
sort(a, lt, gt, d+1);
}
sort(a, gt+1, hi, d);
}
private static int charAt(String s, int d) {
if (d < s.length()) {
return s.charAt(d);
} else {
return -1;
}
}
private static void exch(String[] a, int i, int j) {
String temp = a[i];
a[i] = a[j];
a[j] = temp;
}
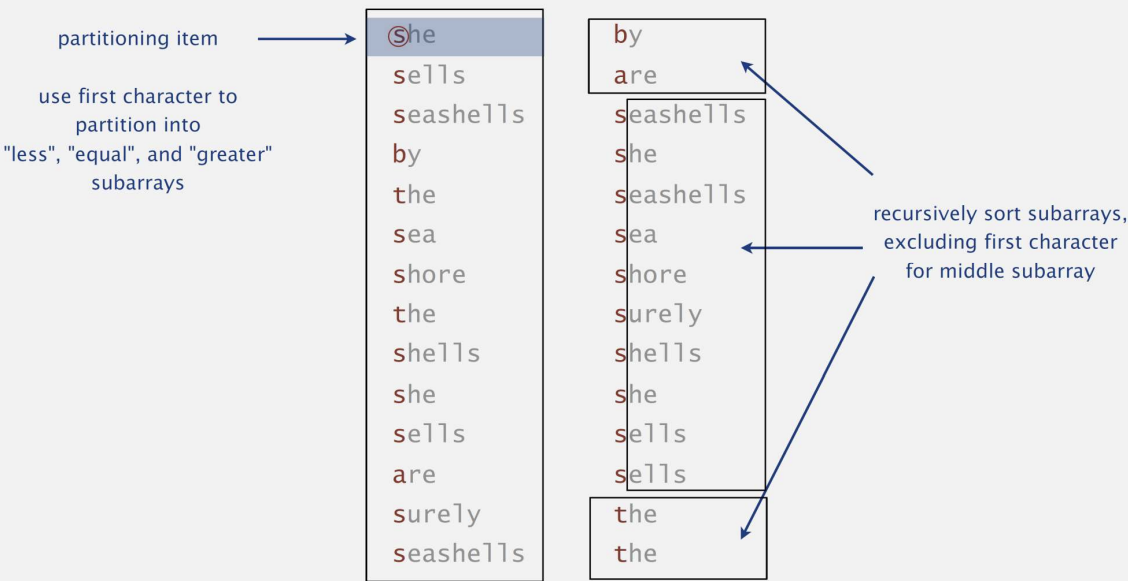
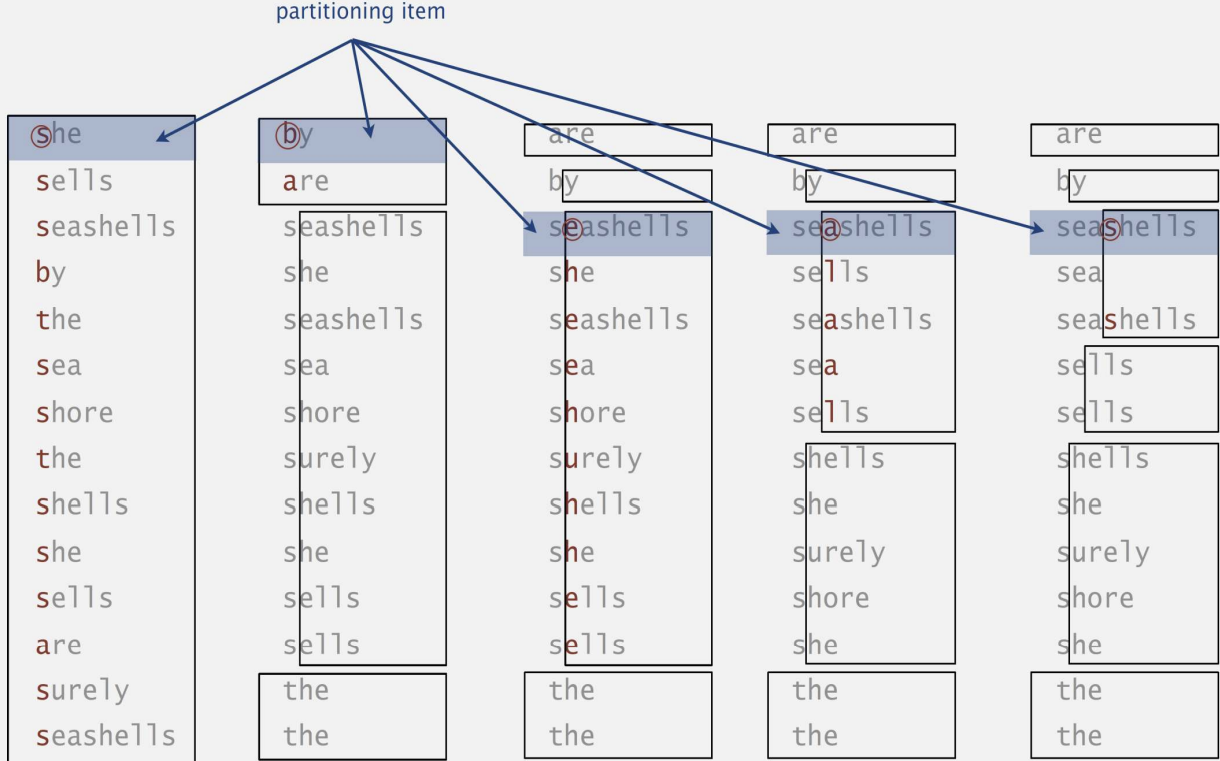
}- d-번째 문자를 이용해 3개의 그룹으로 분할한다.
- MSD 정렬에서 R개의 그룹으로 분할하는 부담을 개선시킬 수 있다.
- 분할 문자와 동일한 문자 그룹에 대해서는 다음 문자를 비교한다.
- 접두사가 매칭되는 길이가 긴 문자열 배열일 수록 효과적이다.
📌 MSD 정렬과 비교
- MSD String 정렬
- Cache 비효율
- count[] 배열을 저장하고 계산하는 비용
- aux[] 배열을 a[] 배열로 복사하는 비용
- 3-way String QuickSort
- Cache 효율
- 재귀로 인한 공간 비용
- unstable sort
📌 성능
| 알고리즘 | 시간 복잡도 | 공간 복잡도 | Stable | 키 연산 |
| 삽입정렬(insertion) | N^2 | 1 | ✅ | compareTo() |
| 합병정렬(merge sort) | N logN | N | ✅ | compareTo() |
| 퀵정렬(quick sort) | N logN | logN | compareTo() | |
| 힙정렬(heap sort) | N logN | 1 | compareTo() | |
| LSD 정렬 | W(N+R) | N+R | ✅ | charAt() |
| MSD 정렬 | 최악: W(N+R) 평균: N log_R(N) |
N + DR (D: 함수 호출 수) |
✅ | charAt() |
| 3-way String QuickSort |
N logN | charAt() |
공간 복잡도를 못 구해서 GPT한테 물어보긴 했는데, 맞는 지 모르겠어서 그냥 공란으로..