[Algorithm] 트라이(Tries)

📕 목차

1. String Simbol Table
2. 트라이(Tries)
3. 삼진 검색 트라이(Ternary Search Tries: TST)

1. String Simbol Table

• 심볼 테이블
• String 심볼 테이블
• 심볼 테이블 성능

📌 심볼 테이블

(key, value) 쌍을 저장하는 데이터 구조
특정 키와 해당 키에 해당되는 값의 쌍을 삽입
key를 검색어로 제공하면, 이에 대응하는 value를 빠르게 찾아주는 구조
고려 사항
- Generics을 지원해야 한다. (단, 키는 Comparable 인터페이스를 구현할 )
- 중복 키는 허용하지 않는다.
- 키와 값은 null이 될 수 없다.
- 테이블에서 {k1, v1}을 제거하는 경우, k1을 검색해서 삭제하거나 {k1, null}을 고려해볼 수 있음

🟡 SimbolTable Api 간단한 명세 (public class ST<K, V>)

메서드 명	설명
ST()	새로운 테이블 생성
void put(K key, V value)	(key, value) 쌍을 테이블에 삽입
V get(K key)	key에 해당되는 값을 반환
boolean contains(K key)	key에 해당되는 값이 있으면 true
void delete(K key)	테이블에서 key의 쌍을 삭제
boolean isEmpty()	테이블이 비어있으면 true
int size()	(key, value) 쌍의 수를 반환
Iterator<K> keys()	테이블에 저장된 모든 키를 반환

📌 String 심볼 테이블

key가 String인 SimbolTable은 다음과 같이 구상해볼 수 있다.

클래스명은 대충 StringST<V>로 지어주도록 하자.

return	메서드 정의	설명
StringST()	StringST()	심볼 테이블 생성
void	put(String key, V value)	key-value 쌍을 테이블에 추가 (value가 null이면 key 삭제)
V	get(String key)	key에 해당하는 value 검색
void	delete(String key)	key-value 쌍을 테이블에서 삭제
boolean	contains(String key)	key가 있으면 true
boolean	isEmpty()	테이블이 빈 경우 true
String	longestPrefixOf(String s)	s의 접두사이면서 가장 긴 key 반환
Iterable<String>	keysWithPrefix(String s)	s를 접두사로 가지고 있는 모든 키를 반환
Iterable<String>	keysThatMatch(String s)	s와 매치되는 모든 키를 반환 (wild character = '.')
int	size()	테이블에 저장된 key-value 쌍의 개수
Iterable<String>	keys()	테이블에 저장된 모든 키 반환

public interface StringST<V> {
    /**
     * key에 val을 저장한다.
     * val이 null이면 key를 삭제한다.
     */
    void put(String key, V val);

    /**
     * key에 대한 값을 반환한다.
     */
    V get(String key);

    /**
     * key-value 쌍을 삭제한다.
     */
    void delete(String key);

    /**
     * key가 존재하는지 여부를 반환한다.
     */
    boolean contains(String key);

    /**
     * 테이블이 비어있는지 여부를 반환한다.
     */
    boolean isEmpty();

    /**
     * s의 접두사 중 가장 긴 키를 반환한다.
     */
    String longestPrefixOf(String s);

    /**
     * s를 접두사로 가지는 키들을 반환한다.
     */
    Iterable<String> keysWithPrefix(String s);

    /**
     * s와 매치되는 키들을 반환한다.
     * .은 와일드 카드로 사용된다.
     */
    Iterable<String> keysThatMatch(String s);

    /**
     * 테이블의 모든 키를 반환한다.
     */
    int size();

    /**
     * 테이블의 모든 키를 반환한다.
     */
    Iterable<String> keys();
}

📌 String 심볼 테이블 성능

그럼 이제 위 심볼 테이블을 어떤 자료구조를 사용해서 만들 것인지가 관건이 된다.

가장 먼저 떠올릴 수 있는 자료구조는 이진 탐색 트리(BST), 최적 이진 탐색 트리(OBST), AVL 트리, 2-3 트리, 2-3-4 트리, Red-Black 트리가 존재한다.

자료구조	검색	삽입	삭제	정렬 지원	키 비교 메서드
BST	logN (최악 N)	logN (최악 N)	logN (최악 N)	✅	compareTo()
OBST	logN	logN	logN	✅	compareTo()
AVL 트리	logN	logN	logN	✅	compareTo()
2-3 트리	logN	logN	logN	✅	compareTo()
2-3-4 트리	logN	logN	logN	✅	compareTo()
Red-Black 트리	logN	logN	logN	✅	compareTo()
해시 테이블	1 (최악 N)	1 (최악 N)	1 (최악 N)	❌	equals() hashCode()

위 내용이 틀릴 수 있다.

코드랑 예전에 공부했던 내용들 뒤져가면서 정리한 건데, 너무 헷갈림.

해시 테이블이 가장 빠른 연산이 가능하긴 하지만, 키의 순서를 유지하지 않기 때문에 정렬된 순서로 데이터를 저장하거나 검색하는 용도로는 사용할 수 없다.

레드 블랙 트리를 사용하자니 매 연산마다 문자열 전체를 비교하며, 각 연산마다 O(L) (여기서 L은 문자열 길이)의 시간이 추가로 소요되므로, 문자열 길이가 길어질 수록 성능이 저하된다.

따라서 우리는 위의 성능 향상 방안을 위해 문자열 정렬처럼 전체 키에 대한 비교를 피하는 쪽을 고민해봐야 한다.

💡 BST보다 빠르면서, Hashing보다 유연하게!

2. 트라이(Tries)

• 트라이
• 검색 연산
• 삽입 연산
• 삭제 연산
• 성능

📌 트라이

public class TrieST<V> implements StringST<V> {
    private static int R = 256; // 기본적으로 ASCII 문자셋을 사용한다.
    private Node root;
    private int N; // trie 안의 key 개수. size() 함수에서 사용하기 위함.

    private static class Node { // Node에 문자는 저장하지 않는다.
        private Object val; // val이 null이 아니면, 그곳까지의 key가 존재한다.
        private Node[] next = new Node[R];
    }
    
    ...
}

Trie는 문자열을 효율적으로 저장하고 탐색하기 위한 트리 형태의 자료구조다.
Trie도 retrieval tree(탐색 트리)에서 따온 단어. (Radix Tree, Prefix Tree라고도 한다.)
각 노드에서 자식들에 대한 포인터들을 배열로 저장하기 때문에 메모리 측면에서 비효율적일 수 있다.

📌 검색 연산

public class TrieST<V> implements StringST<V> {
    ...

    @Override
    @SuppressWarnings("unchecked")
    public V get(String key) {
        Node x = get(root, key, 0);

        if (x == null) {
            return null;
        }

        return (V) x.val;
    }

    private Node get(Node x, String key, int d) {
        if (x == null) {
            return null;
        }

        if (d == key.length()) {
            return x;
        }

        char c = key.charAt(d); // d번째 문자를 이용해 다음으로 이동한다.
        return get(x.next[c], key, d+1);
    }
    
    ...
}

탐색은 문자열의 각 character를 사용해 내부적으로 재귀 함수를 호출한다.
가장 처음에 Head의 child에 key의 첫 번째 문자가 존재하는 지 판단하고, 다음 노드로 이동한다.

🟢 검색 성공

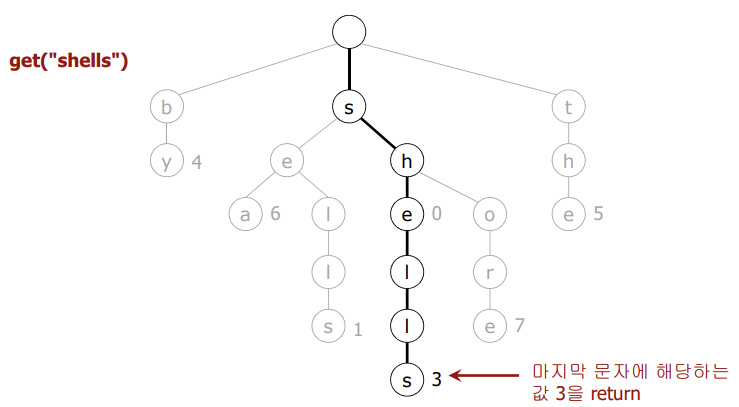
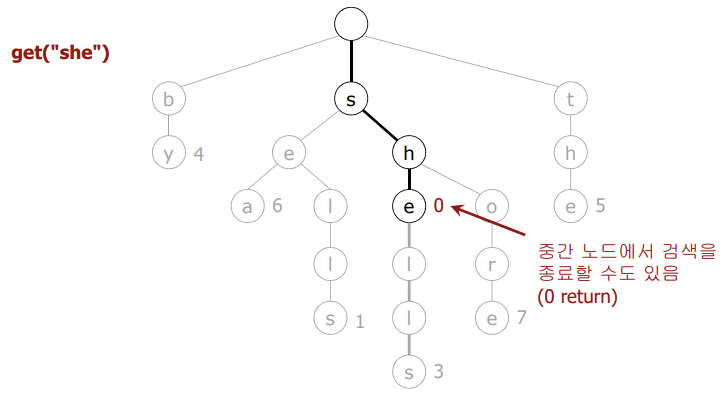
값이 null이 아닌 노드에서 검색이 끝난다면 해당 Node를 반환할 것이고, 최종적으로 Node의 val을 반환하면 된다.
만약 도중에 원하는 문자를 찾아냈으면, 해당 Node를 반환한다.

🔴 검색 실패

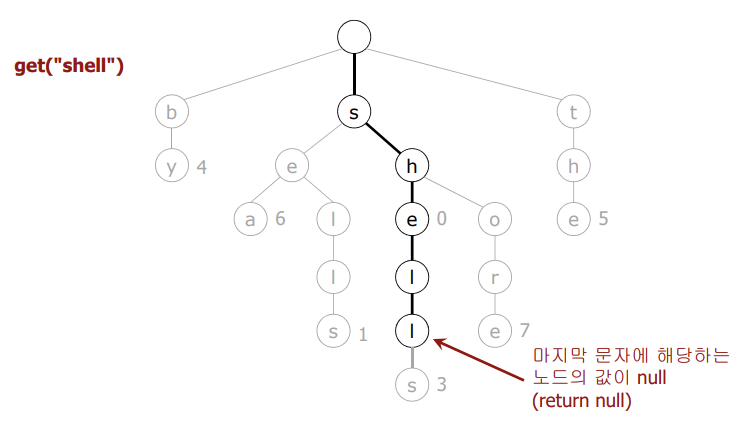
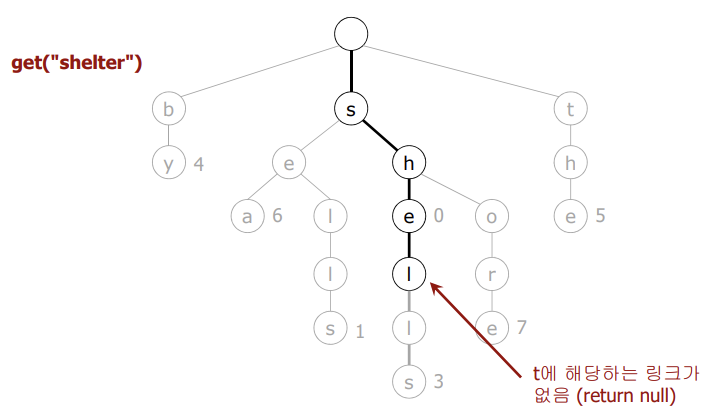
null 링크에서 탐색이 종료되는 경우 null을 반환한다.
null인 노드에서 탐색이 종료되었을 때도 null을 반환한다.

📌 삽입 연산

public class TrieST<V> implements StringST<V> {
    ...

    @Override
    public void put(String key, V val) {
        if (val == null) {
            delete(key);
        } else {
            root = put(root, key, val, 0);
        }
    }

    private Node put(Node x, String key, V val, int d) {
        if (x == null) {
            x = new Node(); // null link인 경우 새로운 노드를 생성한다.
        }

        if (d == key.length()) {
            if (x.val == null) {
                N++; // 새로운 key를 추가하는 경우에만 N을 증가시킨다.
            }

            x.val = val; // key의 끝에 도달하면 val을 저장한다. (else면 단순 값 변경)
            return x;
        }

        char c = key.charAt(d); // d번째 문자를 이용해 다음으로 이동한다.
        x.next[c] = put(x.next[c], key, val, d+1);
        return x;
    }
    
    ...
}

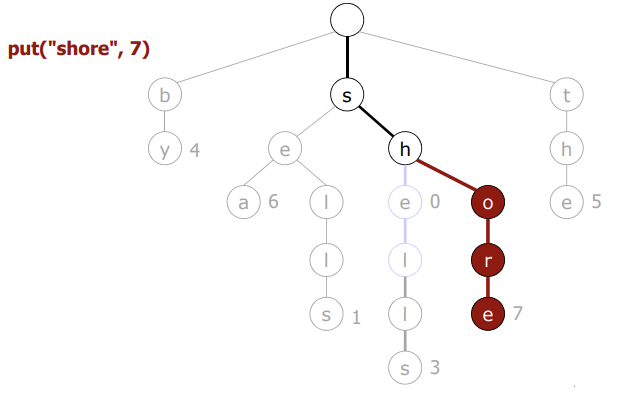
사용자에게 <key, value> 쌍을 받으면, 우선 문자에 대한 link를 생성한다.
- 만약, 이미 link가 존재하는 null Node가 존재하면 값만 넣으면 된다. (N을 1 증가시킨다)
- 만약, 이미 link가 존재하고, value가 할당된 Node가 존재하면 값을 덮어쓴다.

📝 연습 문제

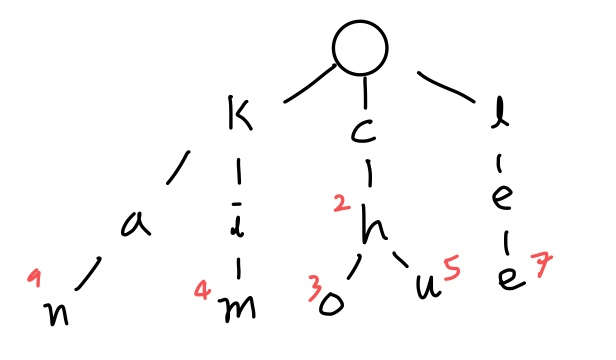
Q: 다음과 같이 (키, 값)의 쌍이 차례대로 입력된 후의 트라이를 그리시오. 단, null link는 그리지 않는다.

(kim, 4) → (ch, 2) → (cho, 3) → (kan, 9) → (chu, 5) → (lee, 7)

📌 삭제 연산

public class TrieST<V> implements StringST<V> {
    ...

    @Override
    public void delete(String key) {
        root = delete(root, key, 0);
    }

    private Node delete(Node x, String key, int d) {
        if (x == null) {
            return null;
        }

        if (d == key.length()) { // 삭제할 노드 도착
            if (x.val != null) {
                N--; // key를 삭제하는 경우에만 N을 감소시킨다.
            }

            x.val = null; // key의 끝에 도달하면 val을 null로 설정한다.
        } else { // 삭제할 노드 도착하지 않은 경우 탐색
            char c = key.charAt(d); // d번째 문자를 이용해 다음으로 이동한다.
            x.next[c] = delete(x.next[c], key, d+1);
        }

        // link 삭제 여부 판단 (현재 노드의 val이 null이고, 자식이 없는 node인 경우)
        if (x.val != null) {
            return x; // x.val이 null이 아니면, x를 반환한다. (삭제 불가)
        }

        for (int c = 0; c < R; c++) {
            if (x.next[c] != null) {
                return x; // null이 아닌 자식이 존재하면 x를 반환한다. (삭제 불가)
            }
        }

        return null; // x.val과 x.next[r]이 모두 null이면, null을 반환한다. (삭제)
    }
}

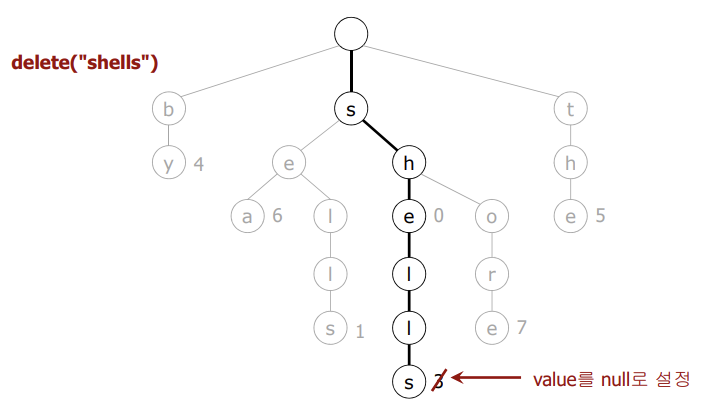
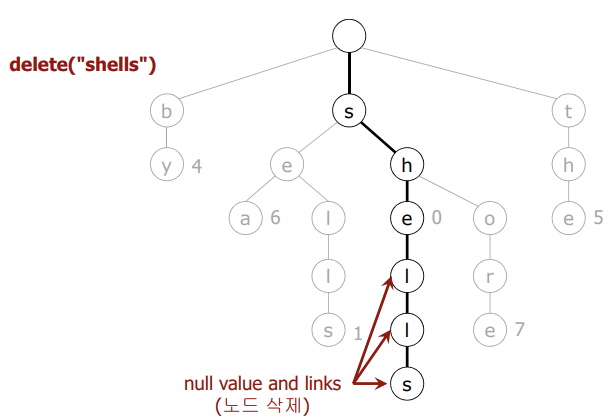
키를 저장한 노드를 발견한 후, 해당 노드의 값을 null로 설정
노드가 null 값을 갖고 모든 링크카 null인 경우, 노드를 삭제한다.

📌 성능

길이가 L인 문자열의 경우, 트라이의 성능은 다음과 같다.

검색 성공: L개의 문자를 모두 비교한다.
검색 실패: L개보다 작은 문자 비교로 키가 없음을 확인할 수 있다.
공간 복잡도
- 모든 노드가 R개의 링크 저장 (Leaf Node 모두 null)
- 길이가 L인 문자열: (L개의 Node) * (R개의 링크/노드)
- 접두사가 유사한 짧은 문자열이 여러 개인 경우 best practice

3. 삼진 검색 트라이(Ternary Search Tries: TST)

• 삼진 검색 트라이
• 검색 연산
• 삽입 연산
• 성능
• TST vs 해싱

📌 삼진 검색 트라이

public class TST<V> implements StringST<V> {
    private Node<V> root;
    private int N;

    private static class Node<V> {
        char c;
        V val;
        Node<V> left, mid, right;
    }
    
    @Override
    public int size() {
        return N;
    }

    @Override
    public boolean contains(String key) {
        return get(key) != null;
    }
    
    ...
}

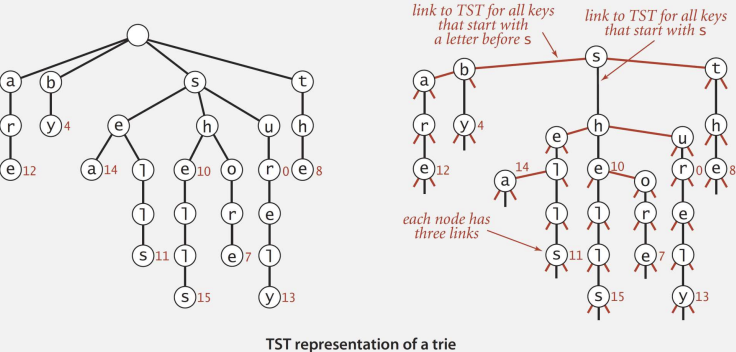
Head가 더 이상 빈 값이 아닌, 처음에 삽입한 문자열의 첫 번째 문자로 시작한다.
트라이의 자식 개수를 3개로 제한하고, 링크는 각각 현재 문자보다 작거나(left), 같거나(middle), 큰(right) 경우로 나뉜다.

📌 검색 연산

public class TST<V> implements StringST<V> {
    ...
    
    @Override
    public V get(String key) {
        Node<V> x = get(root, key, 0);

        if (x == null) {
            return null;
        }

        return x.val;
    }

    private Node<V> get(Node<V> x, String key, int d) {
        if (x == null) {
            return null;
        }

        if (key.length() == 0) {
            return null;
        }

        char c = key.charAt(d);

        if (c < x.c) {
            return get(x.left, key, d);
        } else if (c > x.c) {
            return get(x.right, key, d);
        } else if (d < key.length() - 1) {
            return get(x.mid, key, d + 1);
        } else {
            return x;
        }
    }
    
    ...
}

key의 문자와 Node의 문자를 비교하면서 링크를 탐색한다.
- key 문자 < Node 문자: 왼쪽 링크로 이동
- key 문자 == Node 문자: 중간 링크를 따라가고, key의 다음 문자로 이동
- key 문자 > Node 문자: 오른쪽 링크로 이동

같을 때만 key의 다음 문자를 비교하는 것에 주의하자. 왼/오른쪽 링크 이동은 매칭을 위한 문자를 이동시키지 않는다.

🟢 검색 성공

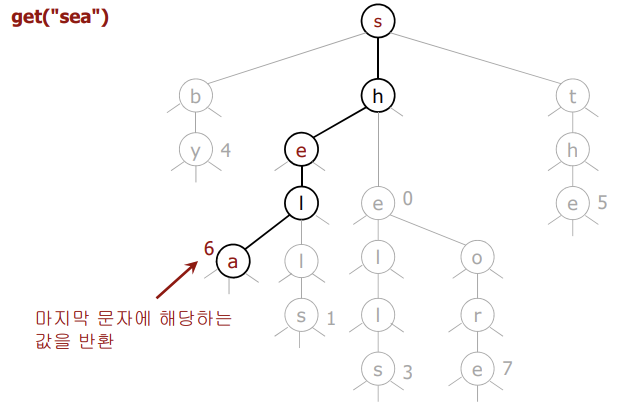
비교가 끝나는 마지막 노드의 val이 null이 아니여야 한다.

🔴 검색 실패

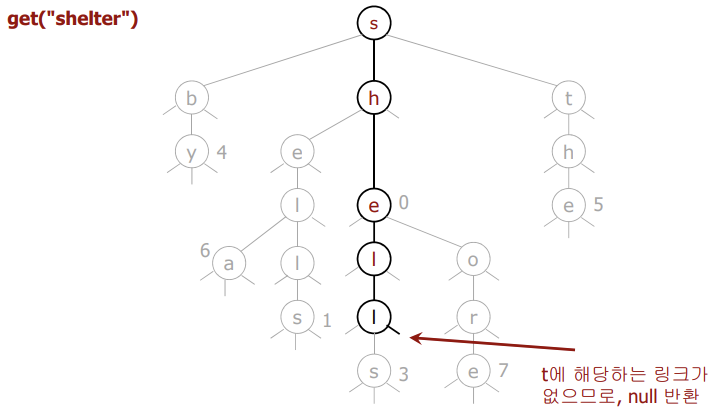
null 링크 혹은 null 노드에 끝나는 경우

📌 삽입 연산

public class TST<V> implements StringST<V> {
    ...

    @Override
    public void put(String key, V val) {
        if (!contains(key)) {
            N++;
        }

        root = put(root, key, val, 0);
    }

    private Node<V> put(Node<V> x, String key, V val, int d) {
        char c = key.charAt(d);

        if (x == null) {
            x = new Node<>();
            x.c = c;
        }

        if (c < x.c) {
            x.left = put(x.left, key, val, d);
        } else if (c > x.c) {
            x.right = put(x.right, key, val, d);
        } else if (d < key.length() - 1) {
            x.mid = put(x.mid, key, val, d + 1);
        } else {
            x.val = val;
        }

        return x;
    }
}

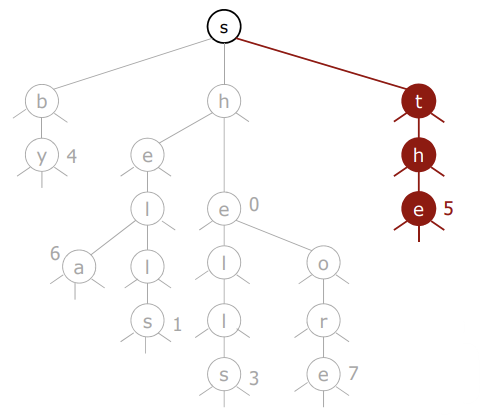
키의 문자들에 대한 검색 연산을 수행하면서 진행
null 링크를 만나면, 새로운 노드를 생성한다.
key의 마지막 문자를 만나면, 해당 노드에 값을 추가한다.

📝 예제

Q: 다음과 같이 (키, 값)의 쌍이 차례대로 입력된 후의 TST를 그리시오. 단, null link는 그리지 않는다.

(kim, 4) → (ch, 2) → (cho, 3) → (kan, 9) → (chu, 5) → (lee, 7)

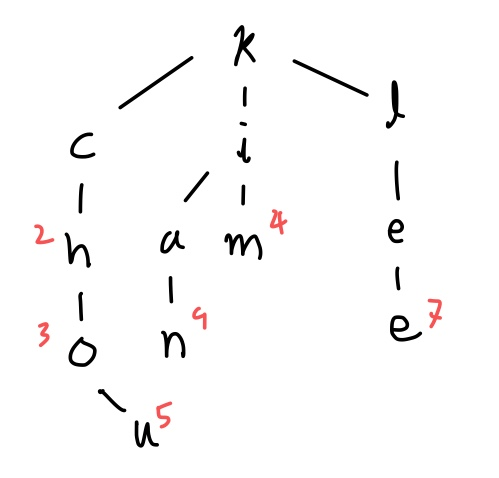
📌 성능

공간 복잡도
- R-way Trie
  - 각 Node마다 R개의 Link 저장
  - L개의 문자로 구성된 문자열: R*L 개의 Link 필요
  - R의 크기가 클 수록 불리하다.
- TST
  - 각 Node마다 3개의 Link 저장
  - L개의 문자로 구성된 문자열: 3*L 개의 Link 필요
시간 복잡도
- R-way Trie
  - L개의 문자 비교
- TST
  - L + logN 개의 문자를 비교 (Tree rotation을 적용할 수 있다.)
  - BST의 경우, logN번의 문자열을 비교

📌 TST vs 해싱

해싱
- key의 모든 문자를 이용하여 해시 값을 계산한다.
- 검색 성공/실패가 거의 동일한 비용 소모
- 해시 함수가 성능 지표에 가장 영향력이 크다.
- key의 순서를 이용하는 연산을 지원 불가
TST
- 문자열 key에 대해서만 적용할 수 있다.
- 검색 실패의 경우, key의 일부 문자만 검사한다.
- key의 순서를 이용한 연산들을 지원한다.

저작자표시 비영리 변경금지

1. String Simbol Table

2. 트라이(Tries)

3. 삼진 검색 트라이(Ternary Search Tries: TST)

티스토리툴바