이번 거 너무 대충 썼다.. 그냥 안 쓰려다가 이미 절반이나 써버려서 그냥 빠르게 머릿속 버퍼에 채우고 버릴 겸 포스팅
📕 목차
1. Introduction
2. Run-length 코딩
3. Huffman 압축
4. LZW 압축
1. Introduction
📌 무손실 압축과 복원

- 메시지: 압축하고자 하는 데이터 B
- 압축: B를 압축한 결과 C(B)를 생성
- 복원: D(C(B)) == B가 되도록 재구성
- 압축률(compression ratio) = C(B)의 크기 / B의 크기
- 텍스트 문서의 경우 50~75% 이상의 압축률
📌 압축의 예시 : 유전자 코드
- 유전자 코드 {A, C, T, G} 4개의 알파벳으로 구성
- 표현 방법
- ASCII 코드로 각 알파벳을 표현할 경우: 문자당 8-bit 소요
- Two-bit 인코딩: 문자당 2bit (A=00, C=01, T=10, G=11) → 압축률 25%
- 고정 길이 코드(Fixed-length code)
- k-bit 코드로 크기가
- k-bit 코드로 크기가
📌 이진 데이터 읽고 쓰기
- 하지만 표준 입력에서 데이터를 읽고 쓰는 최소 단위는 1byte
- bit 단위 파일 입/출력 지원을 하지 않으므로 직접 라이브러리 구현이 필요함
- 압축한 데이터의 경우, bit 단위로 데이터를 액세스 해야 함
따라서 다음과 같은 명세를 따르는 클래스를 구현하여,
byte 단위의 버퍼를 이용해 bit 단위 연산을 지원하도록 만들어야 한다.
📝 BinaryStdIn & BinaryStdOut 명세
| 반환값 | 메서드명 | 설명 |
| boolean | readBoolean() | 1-bit 데이터를 읽어 boolean 값을 반환 |
| char | readChar() | 8-bit 데이터를 읽어 char 값을 반환 |
| char | readChar(int r) | r-bit 데이터를 읽어 char 값을 반환 (byte, short, int, long, double에 대해서도 유사한 메서드 정의) |
| boolean | isEmpty() | 입력 bit 스트림이 비었는지 확인 |
| void | close() | 비트 스트림 닫기 |
| 반환값 | 메서드명 | 설명 |
| void | write(boolean b) | 1-bit 출력 (버퍼링) |
| void | write(char c) | 8-bit 출력 |
| void | write(char c, int r) | c의 하위 r-bit 출력 (byte, short, int, long, double에 대해서도 유사한 메서드 정의) |
| void | close() | 비트 스트림 닫기 |
✒️ BinaryStdIn 구현 일부
public class BinaryStdIn {
static BufferedInputStream in = new BufferedInputStream(System.in);
static final int EOF = -1;
static int buffer; // 한 바이트를 읽어들이는 버퍼
static int n; // 버퍼에 남아있는 비트 수
public static boolean isEmpty() {
return buffer == EOF;
}
public static boolean readBoolean() {
if (isEmpty()) throw new RuntimeException("Reading from empty input stream");
n--;
boolean bit = ((buffer >> n) & 1) == 1; // 버퍼의 가장 왼쪽 비트부터 읽어들인다.
if (n == 0) fillBuffer(); // 버퍼가 비었으면 다시 채워넣는다.
return bit;
}
...
private static void fillBuffer() {
try {
buffer = in.read();
n = 8;
} catch (Exception e) {
System.out.println("EOF");
buffer = EOF;
n = -1;
}
}
}
📌 이진 데이터 출력의 예
❓ 12/31/1999를 출력하는 세 가지 방법
- 문자열
- System.out.print(month + "/" + day + "/" + year);
- 80-bit
- 세 개의 정수
- BinaryStdOut.wite(month); BinaryStdOut.write(day); BinaryStdOut.write(year);
- 4-byte(정수) * 3 * 8-bit/byte = 96-bit
- 4-bit 필드(12), 5-bit 필드(31), 12-bit 필드(1999)
- BinaryStdOut.write(month, 4); BinaryStdOut.write(day, 5); BinaryStdOut.write(year, 12);
- 21-bit (+ close를 위한 3-byte 할당)
🤔 이진 데이터 파일의 내용을 검사하는 방법

- 일반 텍스트 스트림 (Standard Character Stream): 텍스트 파일을 그대로 출력하는 방법
- 0과 1로 표현한 비트 스트림 (Bitstream Represented as 0 and 1 Characters): 파일의 내용을 비트 단위로 읽어 각 비트를 0과 1로 출력
- 16진수로 표현한 비트 스트림 (Bitstream Represented with Hex Digits): 파일의 내용을 16진수로 변환하여 출력한다. 각 byte를 두 자리 16진수로 표현
- 픽셀 이미지로 표현한 비트 스트림 (Bitstream Represented as Pixels in a Picture): 파일의 비트를 픽셀로 변환하여 이미지 형태로 시각
📌 압축 알고리즘 한계
💡 모든 비트 스트링을 압축할 수 있는 알고리즘은 없다.
- 압축 알고리즘 U는 모든 비트 스트링을 압출할 수 있다고 가정
- U(B0) = B1, B1 < B0 ⇾ U(B1) = B2, B2 < B1, ⋯
- 이렇게 계속 압축하면 언젠가는 0 비트 스트링에 도달할 수 있으므로, 모든 비트 스트링은 0-bit로 압축된다는 모순을 갖는다.
2. Run-length 코딩
📌 아이디어

- 0의 수와 1의 수를 k-bit로 표시하고, 매번 교차하는 방법
- k=4일 경우, 15개의 0 & 7개의 1 & 7개의 0 & 11개의 1를 압축하면,
- 1111 0111 0111 1000으로 표현하면 16 bits로 압축 가능 (압축률 = 40%)
🤔 의문점
- k의 크기는 어떻게 정할 것인가?
- 최적의 설정은 입력 텍스트에 따라 가변적이어야 한다. (일단 8로 가정)
- Run length가
- 길이 0인 다른 run이 중간에 있는 것처럼 표시
📌 구현
public class RunLength {
public static void compress() {
char count = 0;
boolean old = false; // 0부터 압축
while (!BinaryStdIn.isEmpty()) {
boolean bit = BinaryStdIn.readBoolean();
if (bit != old) { // 새로운 run 시작
BinaryStdOut.write(count);
count = 0;
old = !old; // 현재 run을 기억
}
else {
if (count == 255) { // run 길이 제한
BinaryStdOut.write(count);
count = 0; // 길이 0인 run 출력
BinaryStdOut.write(count);
}
}
}
BinaryStdOut.write(count);
BinaryStdOut.close();
}
public static void expand() {
boolean bit = false; // 0부터 시작
while (!BinaryStdIn.isEmpty()) {
char count = BinaryStdIn.readChar(); // run 길이가 0~255이므로 8비트씩 read
for (int i = 0; i < count; i++) {
BinaryStdOut.write(bit);
}
bit = !bit; // 0과 1을 toggling
}
BinaryStdOut.close();
}
}
📝 예제
Q: k=4일 때, 0(23개), 1(3개), 0(12개), 1(18개)의 압축 결과와 압축률은? (단, 0부터 시작)
A:
- k=4 이므로, 한 번에 표현 가능한 개수는 15개 ⇾ 0(23)개를 한 번에 표시할 수 없음.
따라서 (1111) (1000) 사이에 길이가 0인 다른 run이 있는 것처럼 표시 ⇾ (1111) (0000) (1000) - 1은 3개이므로 (0011)로 표현 가능
- 0은 12개 이므로 (1100)으로 표현 가능
- 1은 18개이므로, 두 bit로 쪼갠 후 사이에 더미 bit 삽입 ⇾ (1111) (0000) (0011)
∴ 압축 결과 = 1111 0000 1000 0011 1100 1111 0000 0011 , 압축률 = 32/56 = 4/7
3. Huffman 압축
📌 아이디어
💡 빈번히 사용되는 문자는 적은 bit 수로 압축하고, 그렇지 않은 문자들은 bit 수를 많이 할당하는 방법
- 기본 개념: 압축 단위 == 문자
- 가변 길이 코드(variable-length codes) ↔ run-length 코드
- 가변 길이 코드의 문제점
- 압축된 문자열을 어떻게 잘라서 해석할 것인가?
- A=0, B=1, R=00, C=01, D=10, !=11로 압축했다고 가정하자.
ABRACADABRA! = 01000010100100011 ⇾ 0, 1로 읽어야 할 지, 01로 읽어야 할 지 복호화 시점에 알 수 없음
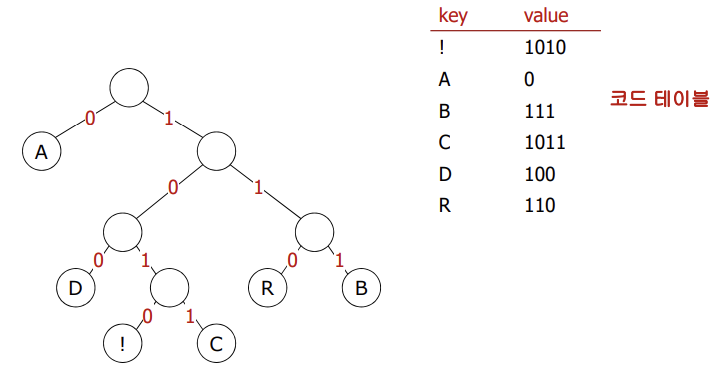
📌 prefix-free code
💡 한 문자의 코드가 다른 문자의 접두사가 되지 않도록 정의하자!
- Huffman 코딩은 각 문자에 대해 최소의 prefix-free code를 생성하는 방법
- 이진 트리 사용
- 2단계 알고리즘
- 각 단어의 발생 빈도수를 사전에 조사하여 int[] freq에 저장
- freq 배열을 이용해 알고리즘 수행
- 압축
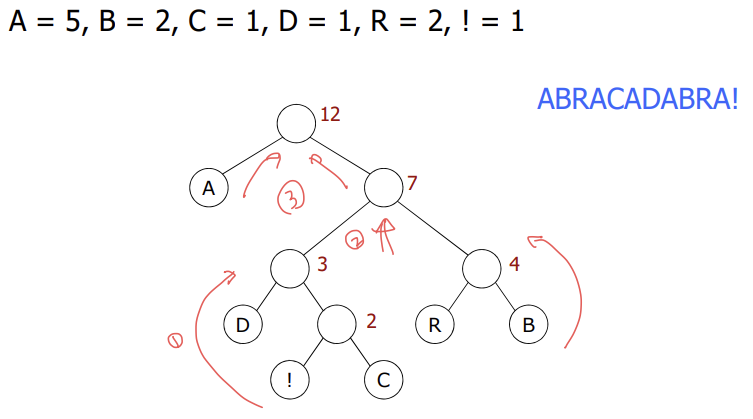
- 발생 빈도수가 적은 단어들을 묶는 이진 트리(Huffman tree) 생성
- 이진 트리를 비트 스트림에 출력 (이후 복원 시 사용)
- 이진 트리를 이용하여 입력 바이트 스트림을 비트 스트림으로 압축
- 복원
- 비트 스트림의 앞부분에 저장된 이진 트리를 복원
- 이진 트리를 이용하여 나머지 비트 스트림을 복원
✒️ 이진 트리 노드 구조
private class Node implements Comparable<Node> {
private char ch;
private int freq;
private final Node left, right;
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
public boolean isLeaf() {
return left == null && right == null;
}
@Override
public int compareTo(Node that) {
return this.freq - that.freq;
}
}우선순위 큐를 사용해야 해서 Comparable을 구현해주어야 한다.
📌 압축 과정
1️⃣ 이진 트리 생성
public class Huffman {
public void compress() {
String s = BinaryStdIn.readString(); // 입력 문자열을 s에 저장
char[] input = s.toCharArray(); // 문자열을 문자 배열로 변환 후, 한 문자씩 처리
int[] freq = new int[R]; // 각 문자에 대한 발생 빈도수를 배열에 저장
for (int i = 0; i < input.length; i++) {
freq[input[i]]++;
}
Node root = buildTree(freq); // 허프만 트리 생성
... // 출력 (4)에서 마저 작성
}
private Node buildTree(int[] freq) {
// Node.freq를 기준으로 오름차순으로 정렬하는 우선순위 큐
PriorityQueue<Node> pq = new PriorityQueue<>();
for (char c = 0; c < R; c++) {
if (freq[c] > 0) {
pq.add(new Node(c, freq[c], null, null)); // 모든 노드가 leaf
}
}
while (pq.size() > 1) {
Node left = pq.remove(); // freq가 가장 작은 두 개의 노드 삭제
Node right = pq.remove();
// 두 개의 노드를 자식으로 하는 부모 노드 생성 후, 우선순위 큐에 추가
Node parent = new Node('\0', left.freq + right.freq, left, right);
pq.add(parent);
}
return pq.remove(); // 우선순위 큐에 하나의 노드(루트 노드)만 남았을 때, 해당 노드 반환
}
...
}
2️⃣ 코드 구축 및 트리 출력
private void buildCode(String[] st, Node x, String s) { // 코드 구축
if (!x.isLeaf()) {
buildCode(st, x.left, s + '0'); // 왼쪽 자식은 prefix 0
buildCode(st, x.right, s + '1'); // 오른쪽 자식은 prefix 1
} else {
st[x.ch] = s; // 리프 노드에서 테이블에 코드 등록
}
}
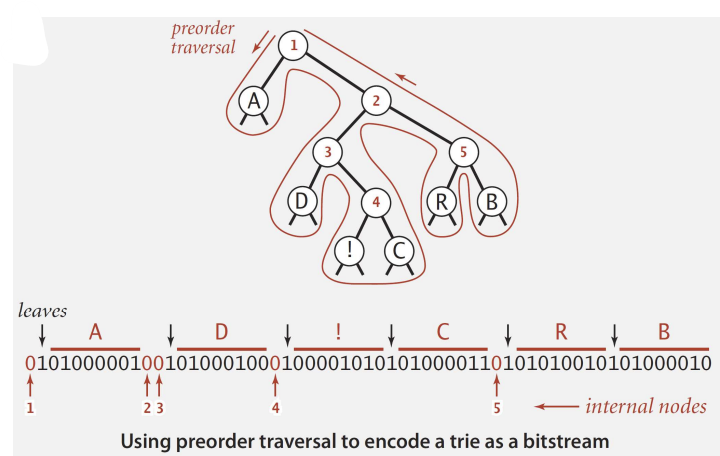
private void writeTrie(Node x) { // 트리 구조를 출력
if (x.isLeaf()) {
BinaryStdOut.write(true); // 리프 노드는 접두사가 1
BinaryStdOut.write(x.ch, 8); // 리프 노드의 문자(8비트) 출력
return;
}
BinaryStdOut.write(false); // non-leaf 노드는 접두사가 0
writeTrie(x.left); // preorder
writeTrie(x.right);
}
3️⃣ 비트 스트림 출력
public void compress() {
String s = BinaryStdIn.readString(); // 입력 문자열을 s에 저장
char[] input = s.toCharArray(); // 문자열을 문자 배열로 변환 후, 한 문자씩 처리
int[] freq = new int[R]; // 각 문자에 대한 발생 빈도수를 배열에 저장
for (int i = 0; i < input.length; i++) {
freq[input[i]]++;
}
Node root = buildTree(freq); // 허프만 트리 생성
String[] st = new String[R]; // 각 문자에 대한 이진 코드를 저장할 배열
buildCode(st, root, ""); // 허프만 코드 생성
writeTrie(root); // 허프만 트리를 출력
BinaryStdOut.write(input.length); // 원본 문자열의 길이 출력
for (char c : input) {
String code = st[c]; // 문자에 대한 허프만 코드
for (int j = 0; j < code.length(); j++) {
// 0이면 false 출력
BinaryStdOut.write(code.charAt(j) == '1'); // 1이면 true 출력
}
}
BinaryStdOut.close();
}
🤔 어째서 pre-order 만으로 복구가 가능하지?
일반적으로 이진 트리를 복구할 때, 단순히 pre-order 또는 post-order 순회 정보만으로는 트리를 재구성할 수 없다.
왜냐하면 순회 방식에 따라 트리 구조가 모호해질 수 있기 때문.
따라서 두 가지 순회 방법을 결합하여 트리 구조를 파일에 써야만 한다.
하지만 허프만 트리의 경우엔 그렇지 않다.
• st['A'] = "00";
• st['B'] = "010";
위와 같이 정했을 때, "01A00AD0111C01R1B"라는 정보만으로 트리를 완벽히 복구할 수 있다.
이는 허프만 트리가 완전 이진 트리로 구현되어 있기 때문이다.
모든 노드의 degree가 2이므로, in-order가 필요없음!!
📌 복원
public void expand() {
Node root = readTree(); // 허프만 트리를 읽음
int N = BinaryStdIn.readInt(); // 원본 문자열의 길이를 읽음
for (int i = 0; i < N; i++) { // 원본 문자열의 길이만큼 반복
Node x = root; // 이진 트리를 루트부터 순회하면서
while (!x.isLeaf()) {
if (BinaryStdIn.readBoolean()) x = x.right; // true이면 오른쪽 자식으로 이동
else x = x.left; // false이면 왼쪽 자식으로 이동
}
BinaryStdOut.write(x.ch, 8); // 리프 노드의 문자 출력
}
BinaryStdOut.close();
}
private Node readTree() {
if (BinaryStdIn.readBoolean()) {
return new Node(BinaryStdIn.readChar(), 0, null, null); // 리프 노드
}
return new Node('\0', 0, readTree(), readTree()); // 내부 노드
}
4. LZW 압축
📌 아이디어
- (입력 key, W-bit 고정 길이 코드) 쌍을 저장할 ST 생성
- 초기에 128개의 단일 문자에 대한 코드를 ST에 저장
- alphabet은 7-bit를 할당하여 표시
- 128은 EOF로 할당
- W(=12 가정) 129~4095 bit에 대해서는 자주 쓰이는 단어를 저장
- 연속된 입력 문자열이 ST에 있을 때까지 계속 문자열 s에 추가
- s = longest prefix match in ST ⇾ trie를 이용할 수 있다!
- s에 해당하는 W-bit 코드를 출력
- 입력의 다음 문자가 c라면, s+c를 ST에 등록하고 새로운 코드 할당.
⚔️ Huffman 압축과 차이점
- Huffman 압축 단위 = 문자
- LZW 압축 단위 = 문자 집합
- 압축 시, 코드 테이블(이진 트리)을 저장할 필요가 없다.
📌 압축 예시

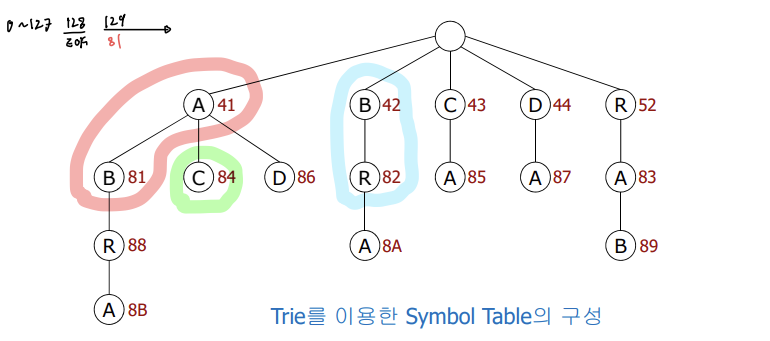
- 일반적인 알파벳은 128-bit로 이미 표현해둔 값을 사용한다.
- A가 65가 아니라 41인 이유는 16진수 표기법을 따르기 때문이다.
- "AB"를 읽으면 "A"와 "B"그리고 "AB"가 트리에 연결된다.
- 이때 "AB"는 129-bit를 16진수로 표기한 81을 가장 처음 할당받게 된다.
📌 압축 구현
public class LZW {
private static final int R = 256; // ASCII 문자
private static final int W = 12; // 코드 폭
private static final int L = 4096; // 코드 수 = 2^W
public void compress() {
String input = BinaryStdIn.readString(); // 압축할 문자열들을 한 번에 읽음
StringST<Integer> st = new TST<>(); // TST를 이용해 심볼 테이블 구성
for (int i = 0; i < 256; i++) {
st.put("" + (char) i, i); // ASCII 문자를 심볼 테이블에 저장
}
int code = R + 1; // R = EOF를 표시하기 위한 코드
while (input.length() > 0) {
String s = st.longestPrefixOf(input); // 입력 문자열에서 가장 긴 prefix 찾기
BinaryStdOut.write(st.get(s), W); // s의 encoding 출력
int t = s.length(); // prefix의 길이
if (t < input.length() && code < L) { // 심볼 테이블이 꽉 차지 않았을 때
st.put(input.substring(0, t + 1), code++); // prefix + next char를 심볼 테이블에 추가
}
input = input.substring(t); // prefix를 제외한 나머지 문자열
}
BinaryStdOut.write(R, W); // EOF 출력
BinaryStdOut.close();
}
}
📌 복원
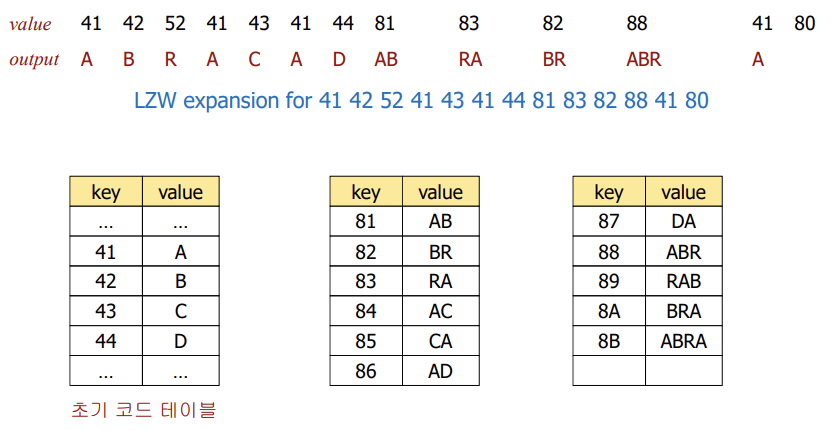
- (W-bit 코드, 문자열 값)의 쌍을 저장하는 ST 생성
- 단일 문자에 해당하는 코드와 값을 ST에 저장
- 압축된 문자열에서 W-bit 코드를 읽는다
- ST에서 해당 코드에 해당하는 값을 찾아서 출력한다.
- 새로운 코드와 값을 ST에 저장한다. (압축과 동일)
이 때, ST의 구성은
⚠️ 주의할 점
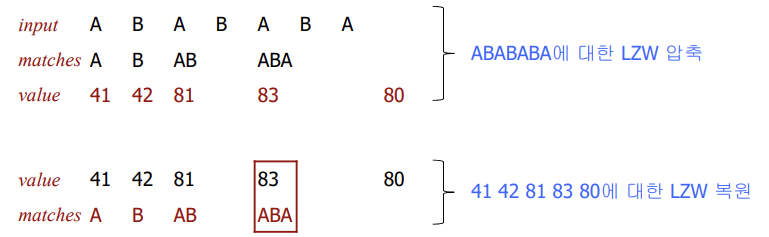
83에 대한 키가 ST에 저장되기 전에 입력에 먼저 등장하는 경우가 존재할 수 있다.
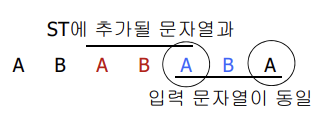
해결 방법은 생각보다 간단한데, 앞선 문자열(AB)과 문자열의 첫 번째 문자(A)를 조합하여 값을 생성하면 된다.
📌 복원 구현
public void expand() {
String[] st = new String[L]; // 심볼 테이블
int i; // 다음 사용할 코드
for (i = 0; i < R; i++) {
st[i] = "" + (char) i; // ASCII 문자 초기화
}
st[i++] = ""; // EOF
int codeword = BinaryStdIn.readInt(W); // 첫 번째 코드
String val = st[codeword]; // 코드에 대한 문자열
while (true) {
BinaryStdOut.write(val); // 출력
codeword = BinaryStdIn.readInt(W); // 다음 코드
if (codeword == R) { // EOF
break;
}
String s = st[codeword]; // 다음 문자열
if (i == codeword) { // special case hack
s = val + val.charAt(0); // special case hack
}
if (i < L) {
st[i++] = val + s.charAt(0); // 심볼 테이블에 추가
}
val = s; // 다음 문자열
}
BinaryStdOut.close();
}
📝 예제
Q: 입력 문자열이 "ABBADABBADABBADOO"일 때, LZW 압축 결과는 무엇인가?
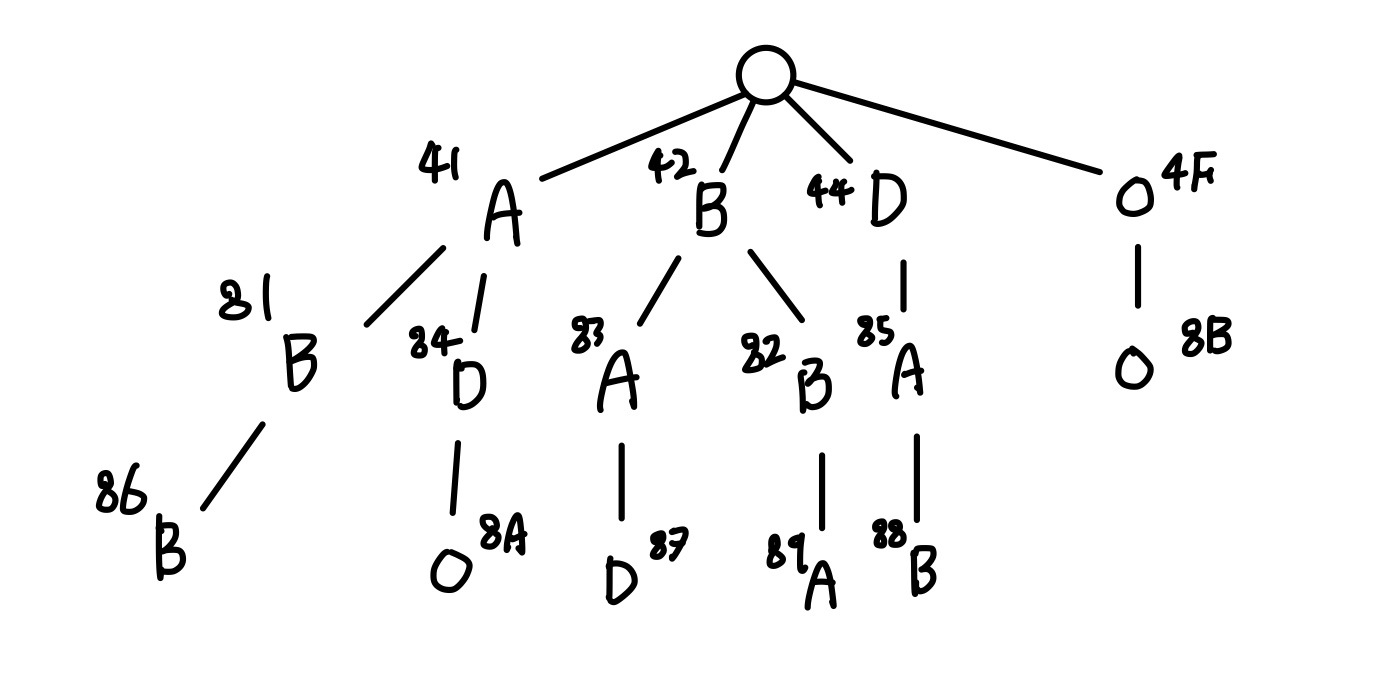
이거 맞나..? 혹시 몰라서 GPT한테 정답 확인해달라고 했더니 맞다고는 하는데, 잘 모르겠다. ㅜ