📕 목차
1. Introduction
2. Brute-force 알고리즘
3. KMP(Knuth-Morris-Pratt) 알고리즘
4. Boyer-Moore 알고리즘
5. Rabin-Karp 알고리즘
1. Introduction
📌 문자열 매칭 문제
| pattern | N | E | E | D | ||||
| text | I | N | S | T | N | E | E | D |
- 길이가 n인 문자열(text)에서 길이가 M인 문자열(pattern)이 존재하는 지 검사하는 알고리즘
- 보통 N >> M 인 경우가 많다.
2. Brute-force 알고리즘
📌 아이디어
- 전탐색 알고리즘답게 패턴을 하나하나 대보고 비교하는 방법!
- 매우 심플하지만, 딱 봐도 느려터졌다.
📌 구현
public class BruteForce {
public static int search(String txt, String pat) {
int N = txt.length();
int M = pat.length();
for (int i = 0; i <= N - M; i++) {
int j;
for (j = 0; j < M; j++) {
if (txt.charAt(i + j) != pat.charAt(j)) {
break;
}
}
if (j == M) {
return i; // 패턴을 찾은 경우 text 위치 반환
}
}
return N; // Not Found
}
public static void main(String[] args) {
String txt = "ABACADABRAC";
String pat = "ABRA";
System.out.println(search(txt, pat));
}
}
📌 동작
- 매번 문자열(N)에 패턴(M)을 대조해보아야 하므로 시간 복잡도는 O(N*M)
- Text와 Pattern이 동일 문자가 반복될 경우, 성능이 저하된다.
- Mismatch가 발생할 경우, text 문자열의 backup이 필요하다.
- 처음 Text 문자열을 검사할 때 4에서 mismatch → 비교 위치를 다시 1로 backup
- Text가 stream 형태로 입력될 경우, 이미 buffer에서 비워졌으므로 처리하기 곤란해짐.
3. KMP(Knuth-Morris-Pratt) 알고리즘
📌 아이디어
- mismatch가 발생했을 때, 비교한 text가 "BAAAAB"라는 것을 알고 있으므로 backup하지 않는 방법
📌 DFA(Deterministic Finite-state Automata)
💡 KMP 알고리즘의 핵심: DFA를 사용하자!
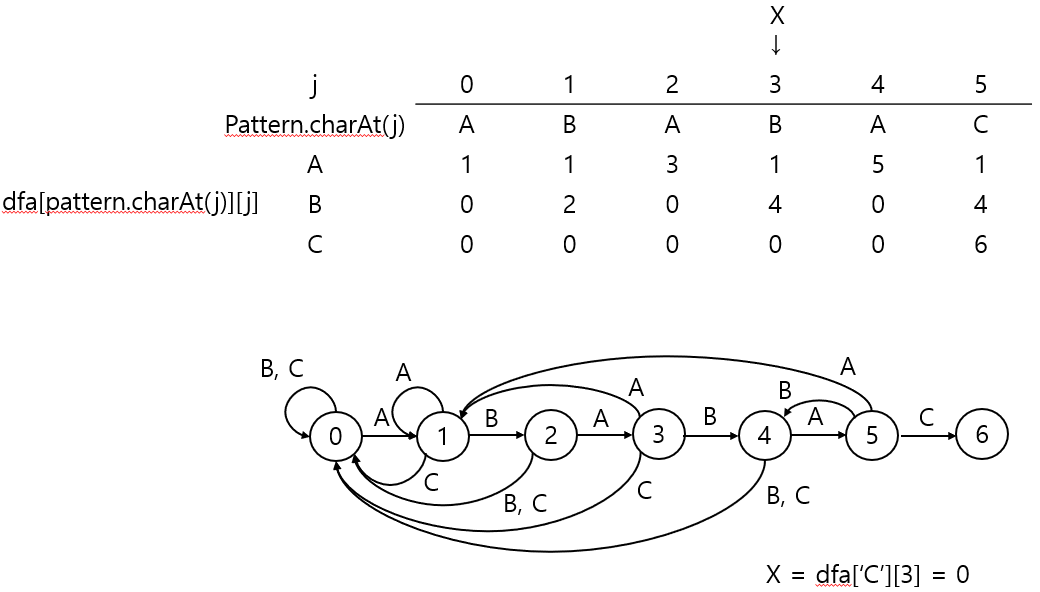
✒️ 배열 표현(dfa[][j])
| j | 0 | 1 | 2 | 3 | 4 | 5 |
| pattern.charAt(j) | A | B | A | B | A | C |
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
- DFA의 상태 == 얼마나 많은 pattern 문자가 매치되었는가?
- 상태 j에서 문자 C를 읽을 경우, j가 종료 상태(6)이면 accept, 아니면 dfa[C][j]로 이동.
- 유한 개의 상태(시작/종료 포함)로 구성
- 모든 문자에 대해 하나의 상태 이동 규칙을 정의
- 종료 상태까지 이동할 수 있는 문자열을 accept한다.
🙄 아니, 이게 뭔 소리여
차근차근 따라가보자.
예를 들어, Text가 "AABACAABABACAA"이라고 가정하자.
패턴은 예시대로 "ABABAC"에 해당한다.
Text의 탐색 위치(i)와 패턴 매칭 상태(j)를 모두 0으로 초기화한다.
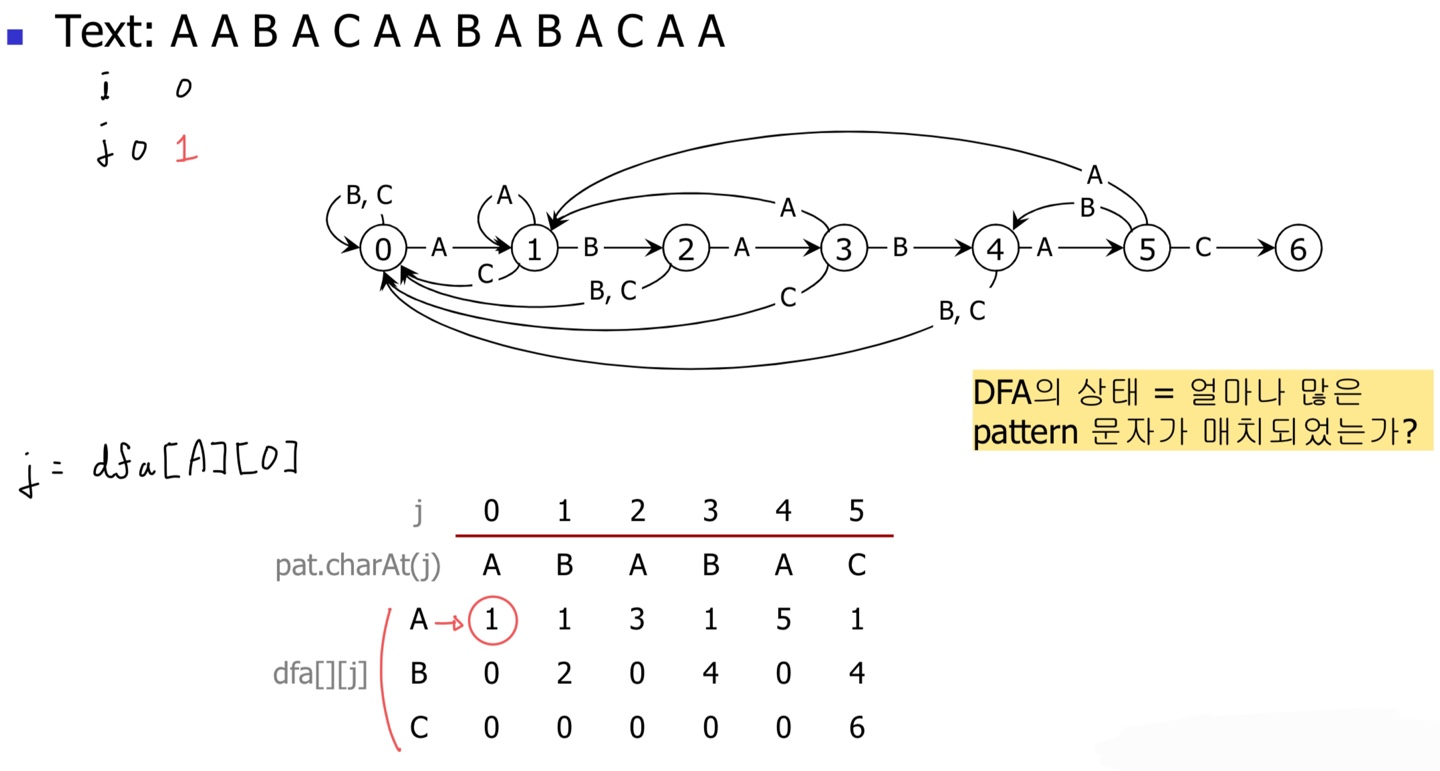
처음 A는 match이므로 상태(j)가 1로 이동한다.
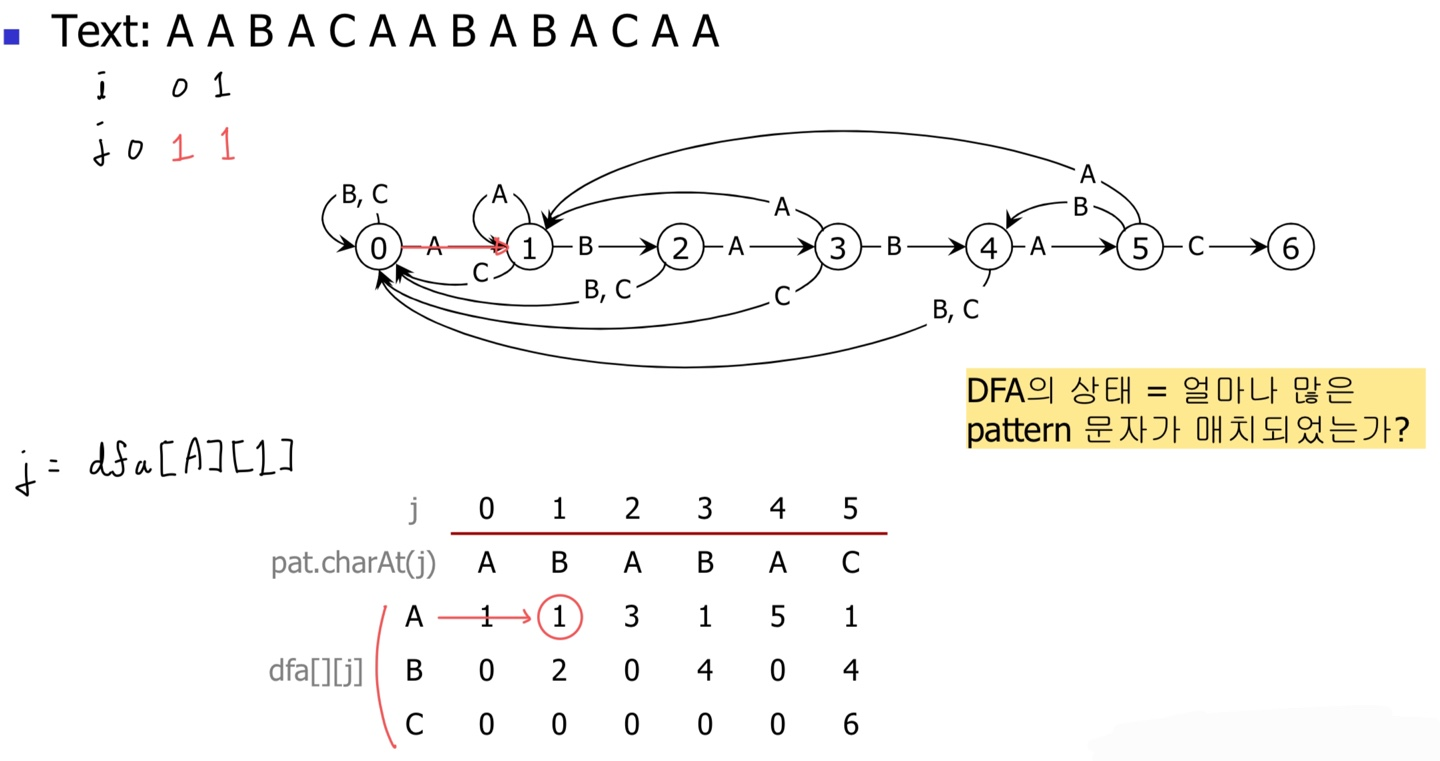
그 다음 mismatch가 발생했으므로 상태를 1로 유지한다.
왜 mismatch가 발생했는데, 상태가 0이 아니라 1로 돌아가는지 의아할 수도 있다.
생각해보면 간단한 이야기다.
만약 현재 Text 문자가 C였다면 상태가 0이 되겠지만, 어차피 A이기 때문에 여기서부터 다시 비교를 시작하는 셈이다.
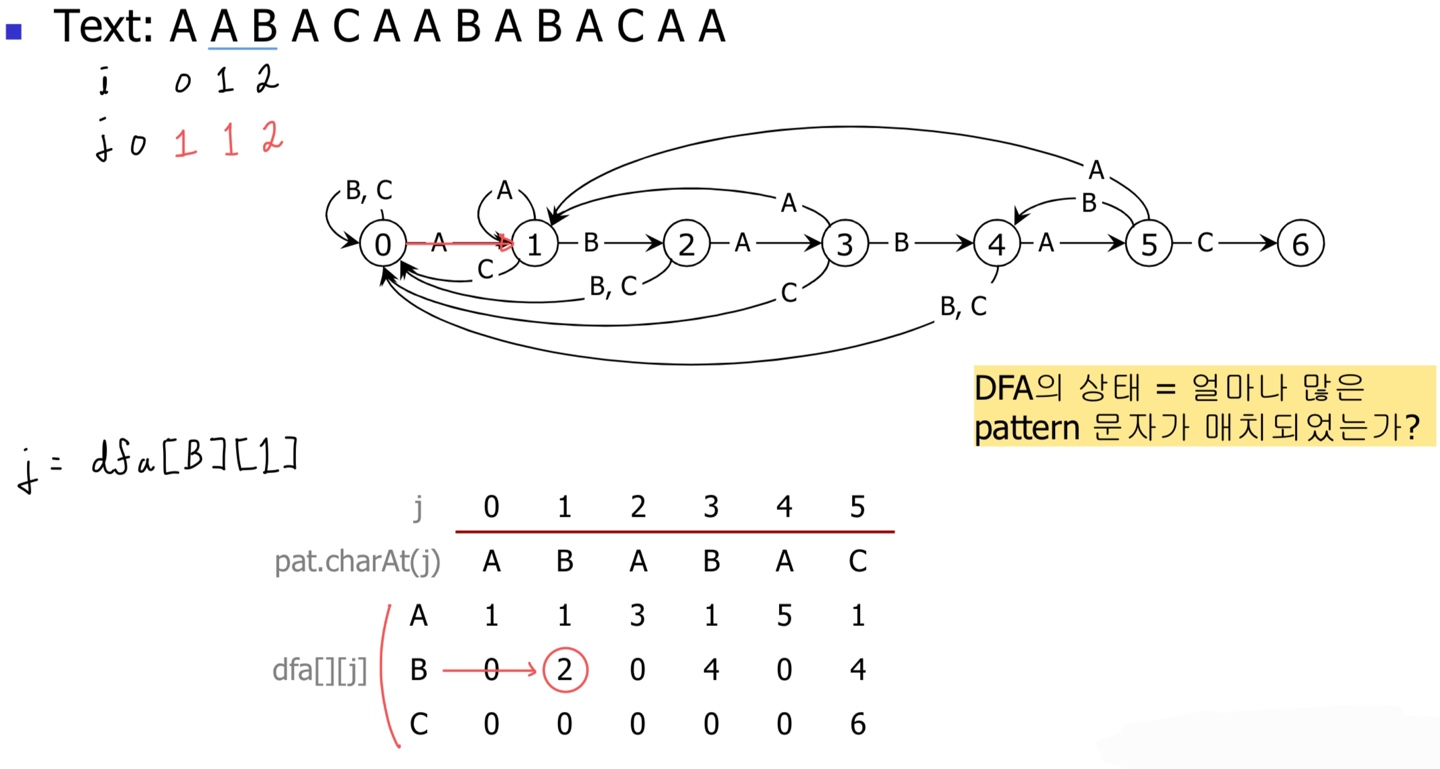
그 다음 B가 나왔기 때문에, dfa[text.charAt(i)][j] == dfa['B'][1]의 값을 확인한다.
당연히 match이므로 상태가 드디어 2로 이동한다.
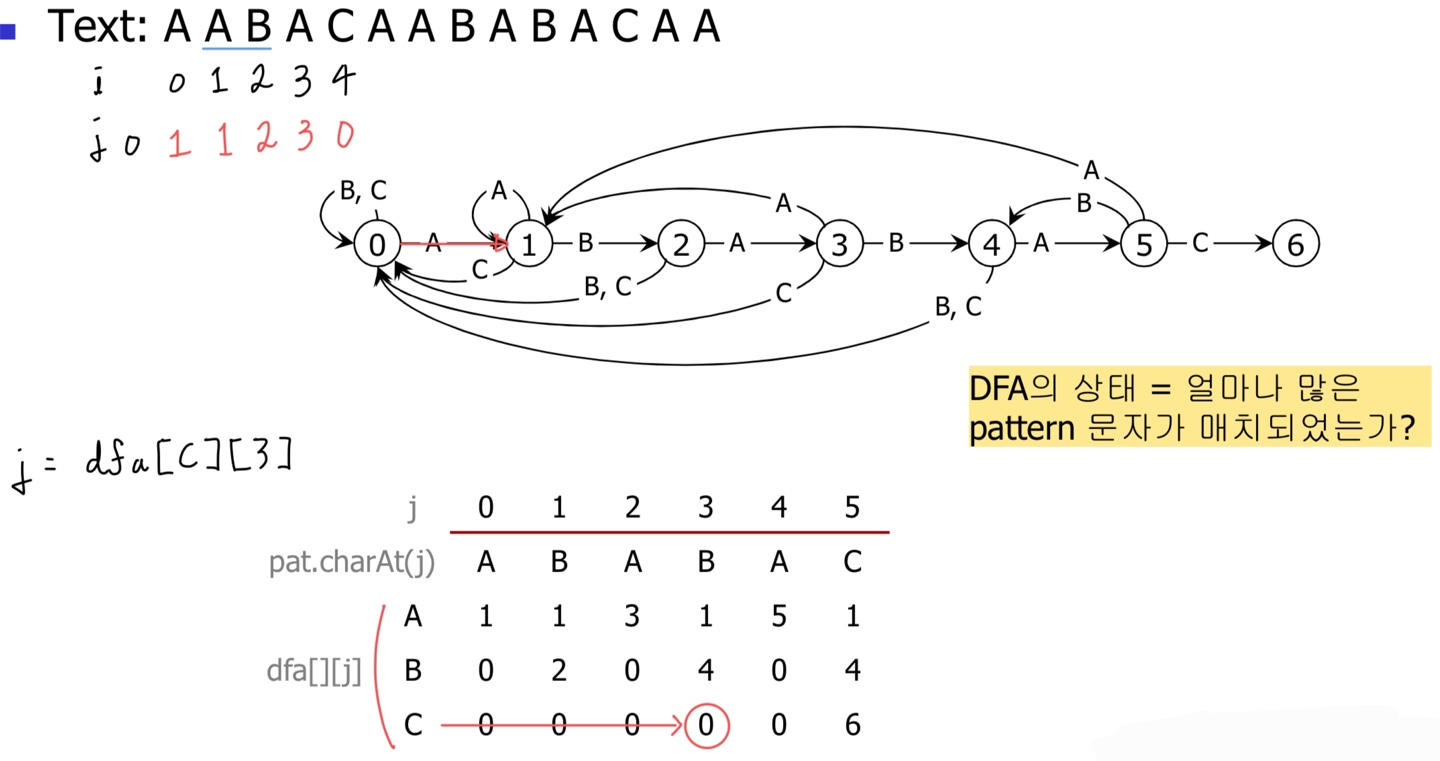
하지만 2번 더 진행하면 C가 등장해서 "ABA" ≠ "ABC"가 되어 실패한다.
설상가상으로 A부터 시작할 수도 없으므로 상태가 0으로 돌아간다.
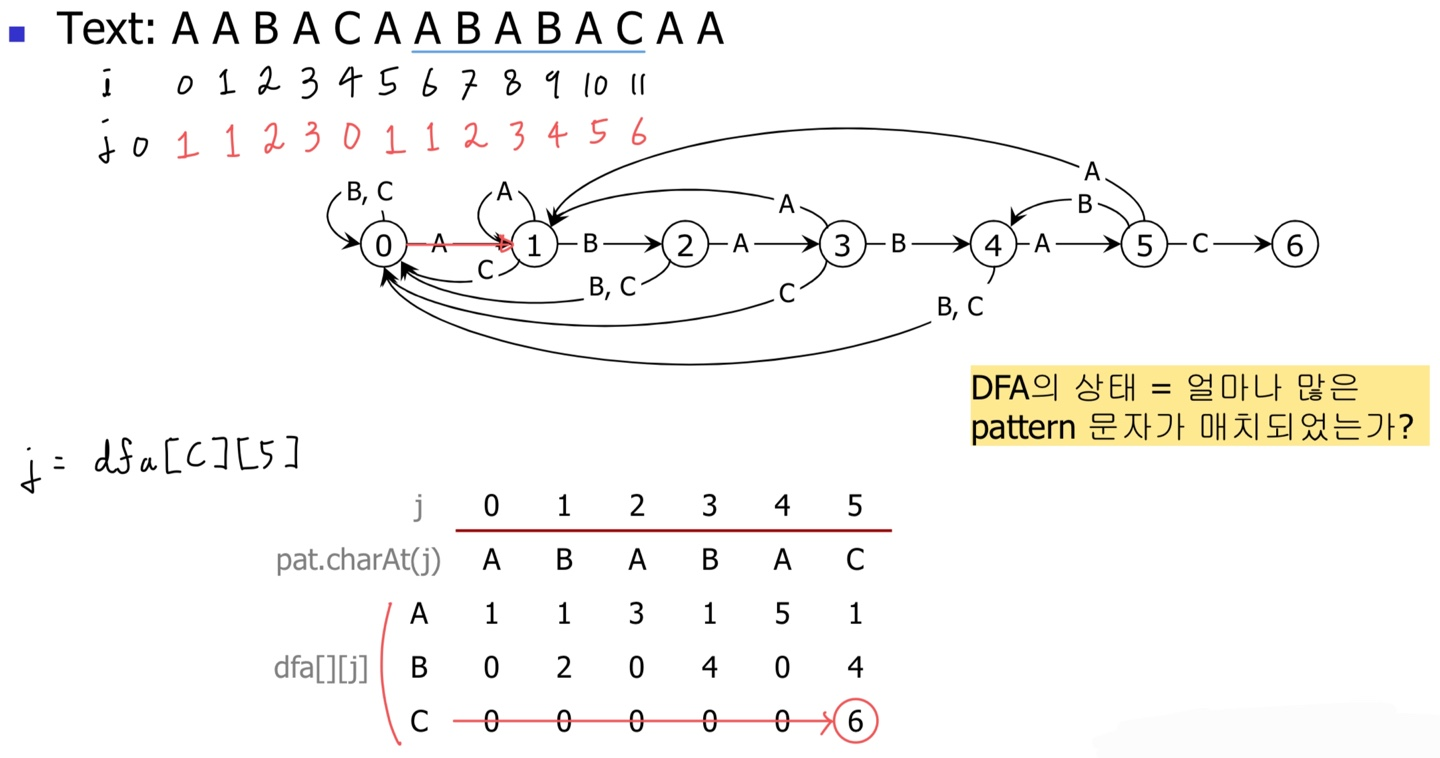
이후 매칭되는 인덱스를 모두 찾으면 종료 상태(j==6)에 도달할 수 있고, 반복문이 종료되면서 해당 인덱스를 반환한다.
✒️ search()
public class KMP {
...
public int search(String txt) {
int i=0, j=0, N = txt.length();
for (i=0; i<N && j<M; ++i) {
j = dfa[txt.charAt(i)][j]; // no backup
}
if (j==M) return i-M; // pattern이 시작되는 text 위치
else return N; // not found
}
}- Brute force와는 달리 Pattern을 dfa[][] 배열로 전처리 과정이 필요하지만, text 포인터 i가 절대 감소하지 않는다.
- 시간 복잡도는 O(N)으로 해결할 수 있다.
📌 DFA 구현
1️⃣ Match transition
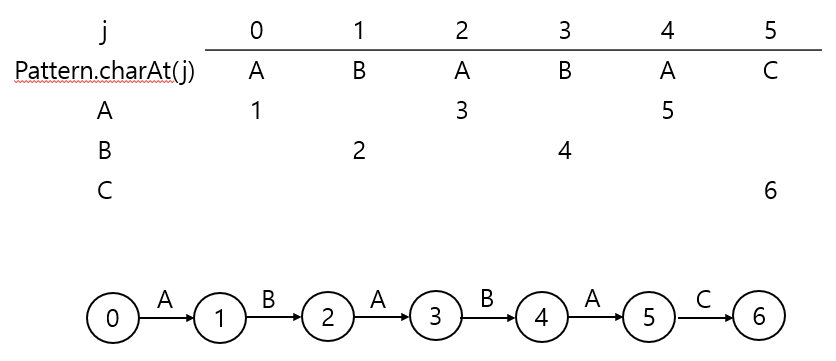
- 상태 j에서 다음 문자 c == pattern.charAt(j)라면, j+1로 이동
2️⃣ Mismatch transition
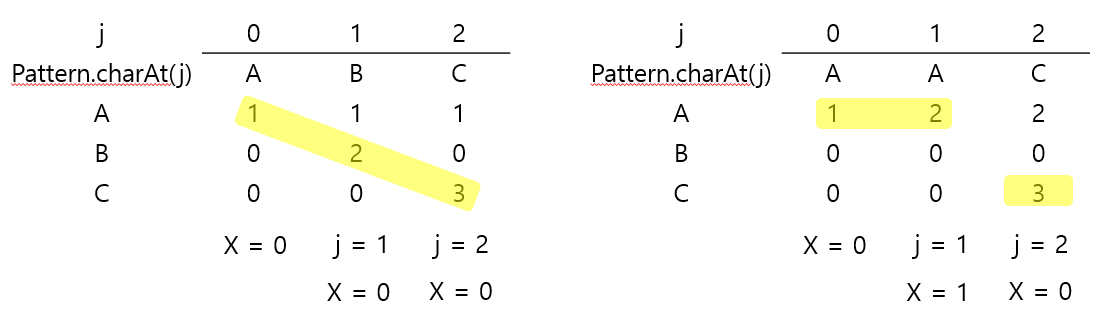
- X < j인 X개의 문자들이 동일하면, X상태에서 다음 문자를 비교
- X의 초기값을 0으로 잡고, X == 0일 때는 pattern.charAt(0) 이외의 문자에 대해서는 상태 이전이 불가
- match transition 이외의 상태 X의 transtition 규칙들을 복사한다.
- X = dfa[pattern.charAt(j)][X]
- 패턴 "AAC"의 j==2에서 A가 나오면 X가 0이 아닌, 1부터 검사할 수 있기 때문
public class KMP {
private final int R; // 기수
private final String pattern; // 패턴
private final int[][] dfa; // DFA
public KMP(String pattern) {
this.R = 256;
this.pattern = pattern;
int M = pattern.length();
dfa = new int[R][M];
dfa[pattern.charAt(0)][0] = 1; // 초기 상태의 match condition
for (int X=0, j=1; j<M; ++j) {
for (int c=0; c<R; ++c) {
dfa[c][j] = dfa[c][X]; // 이전 X 상태의 모든 이동 규칙들을 복사
}
dfa[pattern.charAt(j)][j] = j+1; // match일 경우 다음으로 이동
X = dfa[pattern.charAt(j)][X]; // 현재 상태가 이전의 어디까지 동일한가?
}
}
...
}
✒️ DFA 작성 예시
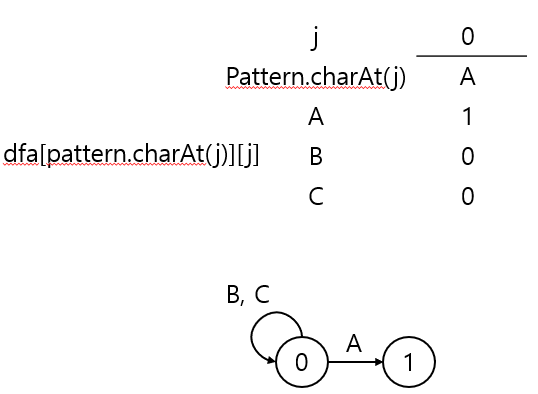
상태 규칙에 의해 X=0일 때는, 'A'에 매칭되는 경우에만 1로 이동 가능
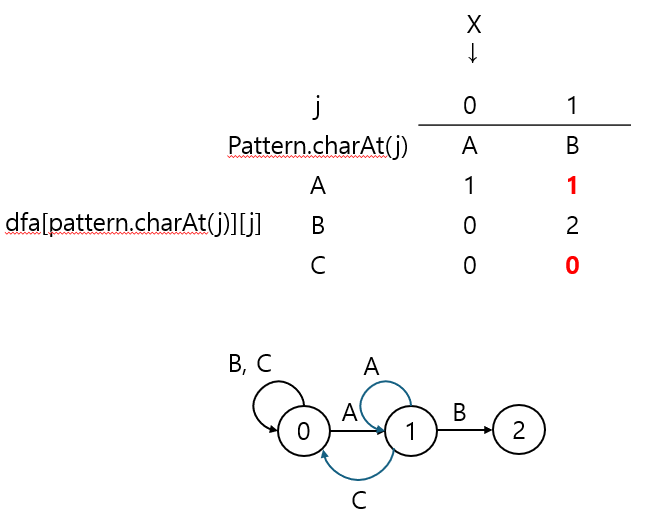
dfa[row][X]의 값을 dfa[row][j]로 복사한 후,
패턴에 매칭되는 'B'에 대해서는 dfa[pattern.charAt(j)][j] = j+1로 상태 전이 시켜준다.
X = dfa[pattern.charAt(j)][X] = dfa['B'][X] = 0이므로 바뀌지 않는다.
식이 이해가 안 된다면 직관적으로 이해하면 된다.
상태 1에서 A가 나온다면, 다시 해당 지점부터 매칭을 비교할 테니 1을 유지한다.
하지만 C인 경우엔 처음부터 매칭을 시작하려 해도 'A'가 아니므로 상태가 0이 되는 것이다.
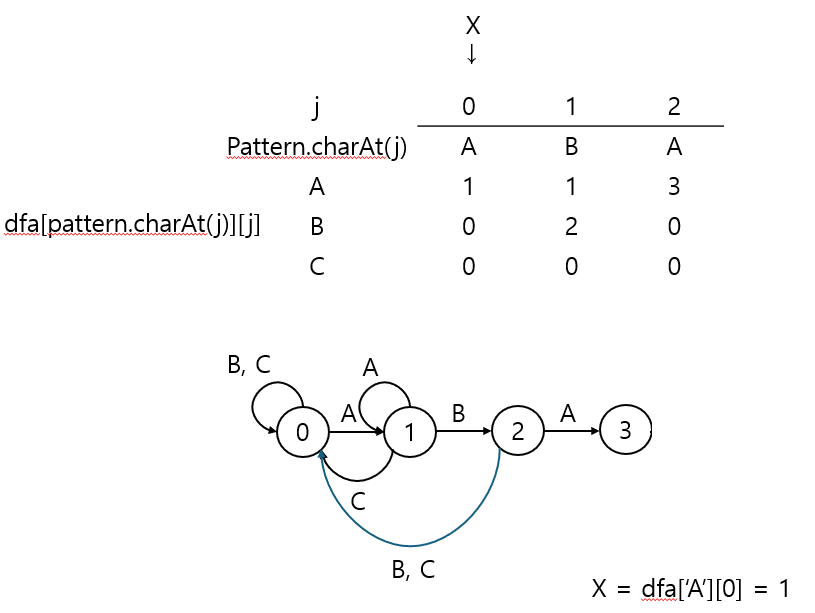
상태 2에서 B, C가 나오면 처음부터 비교하는 것도 불가하므로 모두 상태를 0으로 전이시킨다.
그 다음 해당 지점에 A가 나오면 dfa['A'][X == 0] == 1이되므로, 드디어 X가 업데이트 된다.
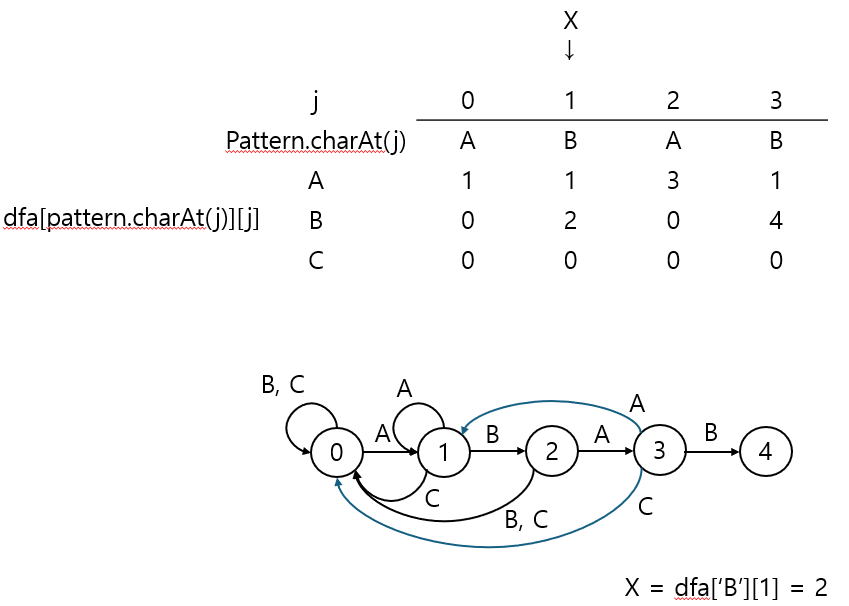
상태를 복사할 때 dfa[row][X]를 복사해오므로, j == 1번 컬럼에 해당하는 {1, 2, 0}을 가지고 온다.
그리고 'B'에 매칭되는 경우 j+1을 할당하여 상태 전이를 시켜준다.
마지막으로 X는 dfa['B'][X == 1] == 2이므로 업데이트 된다.
만약, X가 왜 업데이트 되는지 이해가 안 간다면, 패턴의 "ABAB?"에서 "AB"가 반복되는 것을 생각하면 된다.
"AB"의 'B'에서 실패했을 때와 "ABAB"의 'B' 실패했을 때 모두 match transition 이외엔 동일한 상태 전이를 하게 되기 때문이다.
즉, 패턴 "ABA"에서 다음 "C"가 나왔다면 X = 0이 된다.
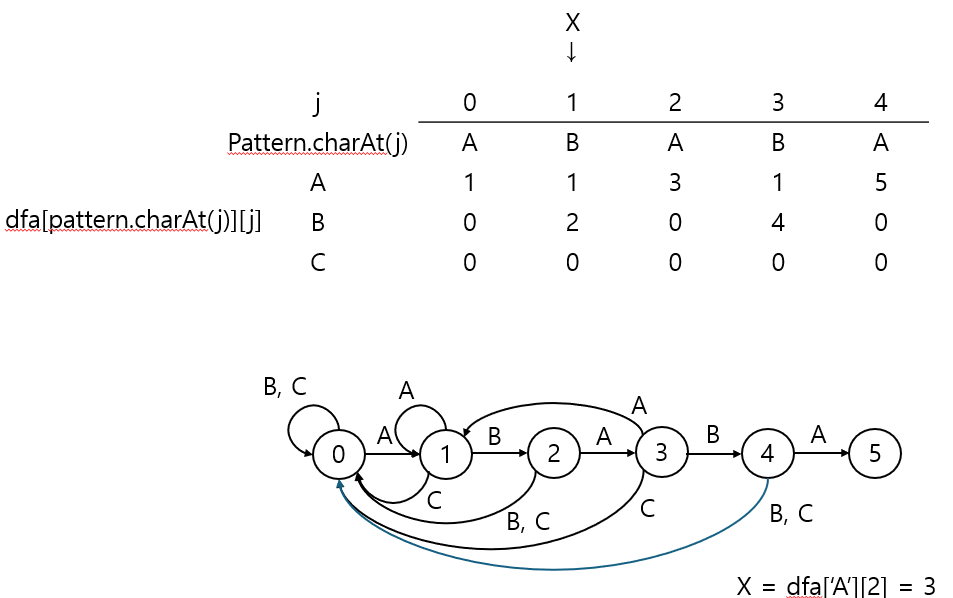
마찬가지로 복사 + match 전이 + X 업데이트를 수행하면 된다.
처음 상태를 복사할 때 dfa[row][X == 3]의 값들을 가져온다.
그리고 dfa['C'][j] = j+1을 해주면 최종 상태에 도달하므로 매칭되는 패턴을 찾았다고 판단할 수 있게 된다.
중요한 건 여기서 X가 0으로 업데이트 된다는 점.
만약 text가 "ABABAB"였다고 하자.
그렇다면 패턴은 "ABAB"까지는 여전히 만족한다고 볼 수 있으므로, j가 0 혹은 1이 아니라 3의 상태값을 복사하는 것이다.
📝 연습 문제
1️⃣ 패턴이 "AACAAB"인 경우의 KMP DFA를 작성하라
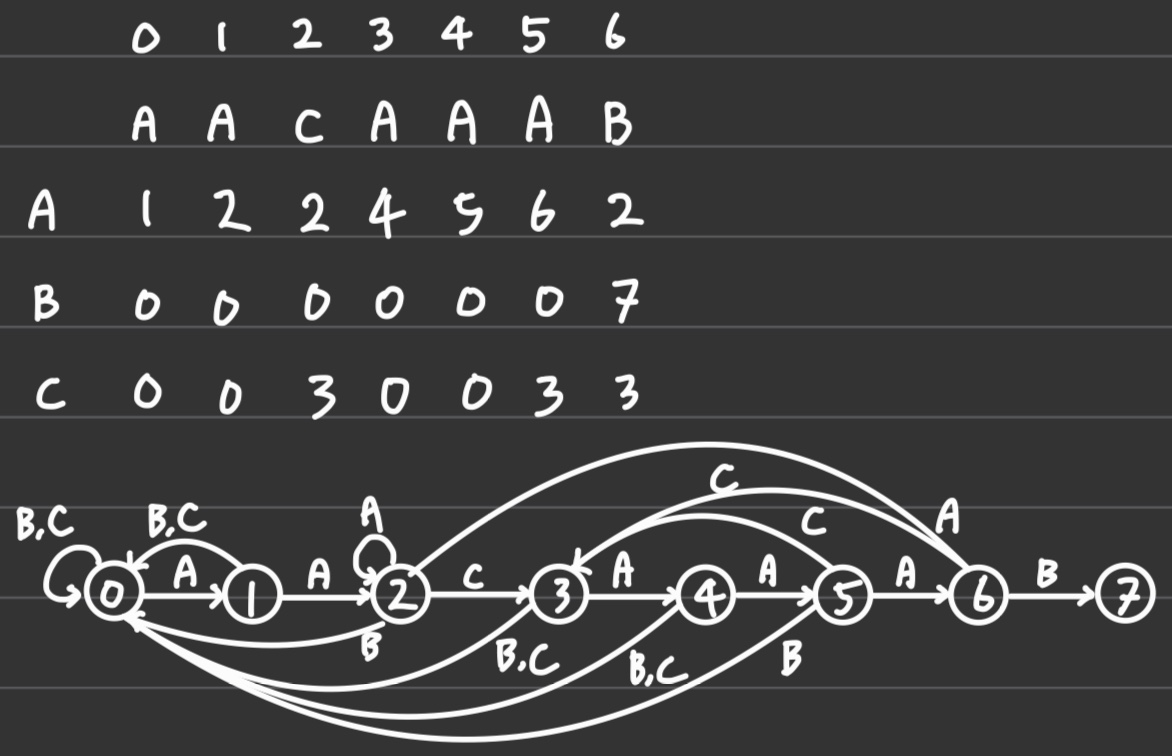
2️⃣ 패턴이 "AABCABAC"인 경우의 KMP DFA를 작성하라
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| A | A | B | C | A | B | A | C | |
| A | 1 | 2 | 2 | 1 | 5 | 2 | 7 | 2 |
| B | 0 | 0 | 3 | 0 | 0 | 6 | 0 | 0 |
| C | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 8 |
4. Boyer-Moore 알고리즘
📌 아이디어
- Pattern의 마지막 문자부터 text와 비교하는 방법
- Text의 비교 문자가 pattern에 포함되지 않으면, M만큼 비교를 skip할 수 있다.
📌 Mismatched Character Heuristic (얼마나 많이 skip해야 하는가?)
1️⃣ Mismatch character가 pettern에 없는 경우
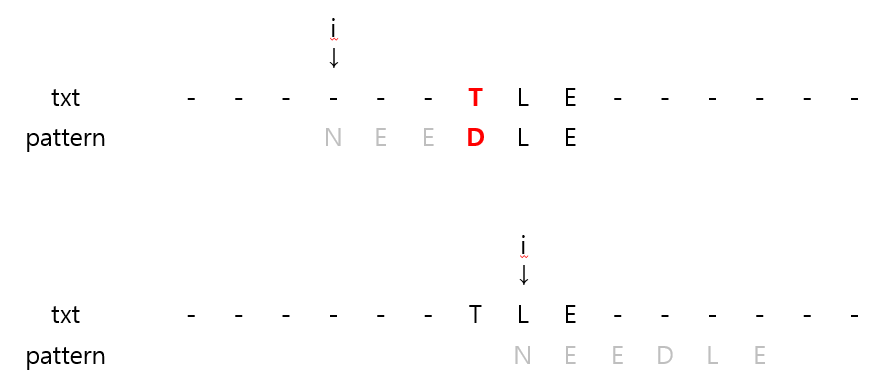
- 'T'는 pattern에 나타나지 않는 문자이므로, 시작 위치를 T 다음으로 완전히 건너뛸 수 있다.
2️⃣ Mismatch character가 pattern에 나타날 경우
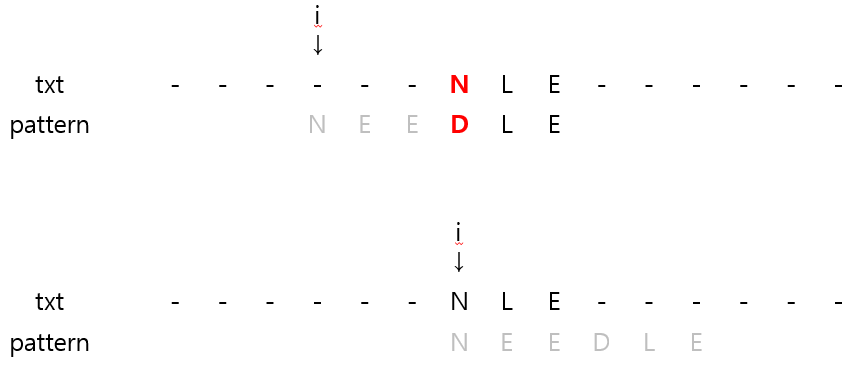
- 'N'은 pattern에 등장하는 문자인데 얼만큼 이동해야 할까?
- 가장 쉽게 생각해볼만한 건 text 'N'을 pattern의 가장 오른쪽에 나타나는 'N'에 맞추는 방법이다.
- 하지만 위의 방법을 적용하면 pattern에 등장하는 'E' 문자의 가장 오른쪽에 맞추게 되면서, i가 왼쪽으로 이동하는 문제가 발생한다.
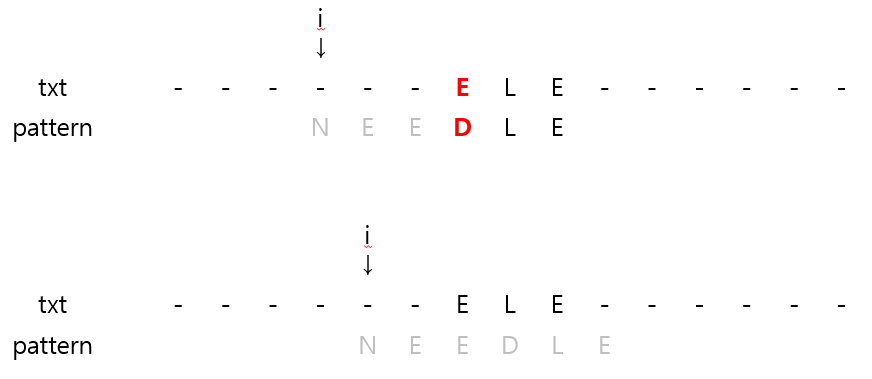
- 이런 경우에는 i를 단순히 1 증가시키는 게 낫다.
- 즉, pattern에 포함되는 mismatch character가 나타났을 때는 가장 마지막 문자로 이동하되, i가 왼쪽으로 이동하게 되면 1 증가하는 방향으로 진행해야 한다.
💡 Pattern의 각 문자에 대해 가장 오른쪽에 나오는 위치를 미리 계산하자
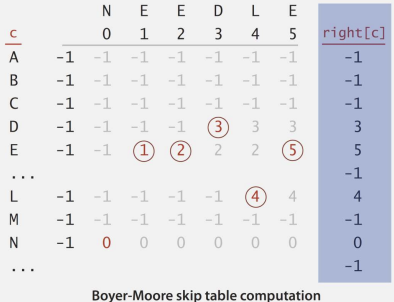
int M = pattern.length();
int R = 256;
right = new int[R];
for (int c = 0; c < R; ++c)
right[c] = -1;
for (int j = 0; j < M; ++j)
right[pattern.charAt(j)] = j;
📌 구현
public class BoyerMoore {
private final String pattern;
private final int[] right;
public BoyerMoore(String pattern) {
this.pattern = pattern;
int M = pattern.length();
int R = 256;
right = new int[R];
for (int c = 0; c < R; c++) {
right[c] = -1;
}
for (int j = 0; j < M; j++) {
right[pattern.charAt(j)] = j;
}
}
public int search(String txt) {
int N = txt.length();
int M = pattern.length();
int skip;
for (int i = 0; i <= N - M; i += skip) {
skip = 0;
for (int j = M - 1; j >= 0; j--) {
if (pattern.charAt(j) != txt.charAt(i + j)) { // 패턴 불일치
skip = Math.max(1, j - right[txt.charAt(i + j)]);
break;
}
}
if (skip == 0) return i; // 패턴을 찾은 경우 text 위치 반환
}
return N; // Not Found
}
}주요하게 봐야할 것은 skip을 할당할 때의 Math.max(1, j - right[txt.charAt(i + j)]); 스니펫이다.
- 패턴에 포함되지 않은 mismatch 문자면 -1이 할당되어 있으므로, 현재 txt index에서 한 칸 이동하면서 점프한다.
- 패턴에 포함되는 mismatch 문자면, pattern의 해당 문자 중 가장 마지막 문자에 맞춰지도록 i를 이동한다.
- 패턴에 포함되는 mismatch 문자지만 i가 왼쪽으로 이동(음수)하면, 단순히 1 증가시킨다.
📌 성능
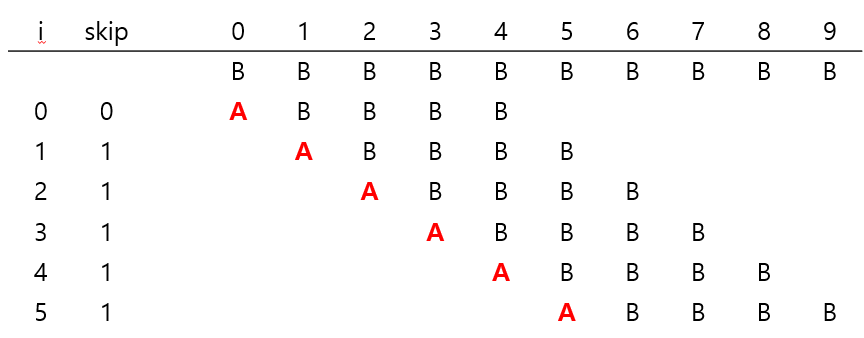
- 일반적인 경우에 Text길이가 N, pattern의 길이가 M이면 ~N/M 개의 문자 비교를 수행한다. O(N)
- 위 이미지처럼 반복적인 패턴이 나타나면 O(NM)의 시간 복잡도를 갖는다.
- 반복적 패턴에 대응하기 위해 KMP 방식 규칙을 추가하면, 최악의 경우에도 O(N)의 문자 비교만 발생한다.
5. Rabin-Karp 알고리즘
📌 아이디어
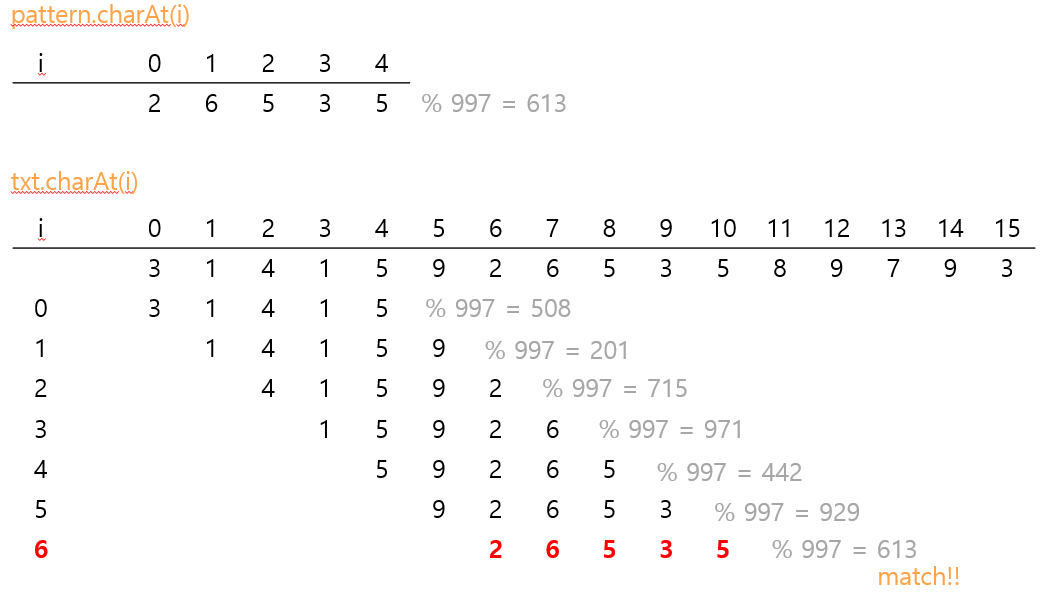
- modular hashing으로 패턴에 대한 해시코드를 구해서 일치 여부를 확인하는 방법
- 각 i에 대해 txt[i...M+1-1]의 해시값을 계산하고, 두 개의 해시값이 동일하면 문자열이 일치하는지 확인한다.
📌 Horner의 방법론
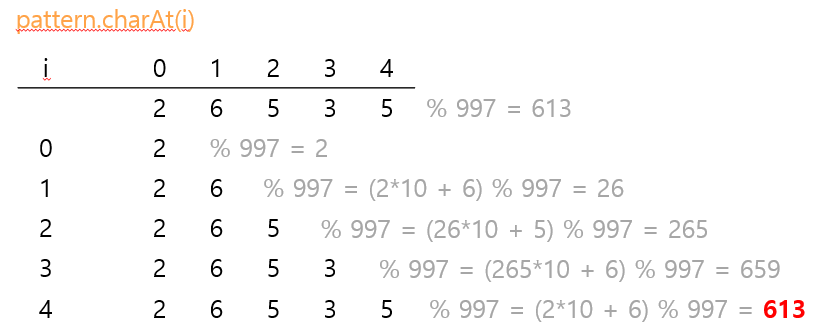
private long hash(String key, int M) { // key[0..M-1]의 해시값 계산
long h = 0;
for (int j = 0; j < M; j++) {
h = (R * h + key.charAt(j)) % Q;
}
return h;
}- Modular 연산 특징
- (a+b) % Q = ((a % Q) * (b % Q)) % Q
ex) (1+20) % 7 = 2 = (3+6) % 7 - (a*b) % Q = ((a % Q) * (b % Q)) % Q
ex) (10*20) % 7 = 4 = (3*6) % 7
- (a+b) % Q = ((a % Q) * (b % Q)) % Q
- Modular 해시 함수
- \(t_{i}\)를 txt.charAt(i)라 가정
- \(x_{i} = (t_{i}R^{M-1} + t_{i+1}R^{M+2} + \dots + t_{i+M-1}R^{0})\) % \(Q\)
- M자리이며, 각 자리는 base-R 정수인 수에 대해 나머지 연산 Q 연산을 수행
📌 효율적인 \(x_{i}\) 구하기 : Rolling hash
처음 딱 들었을 때, "누가 이런 천재적인 발상을 했지?"라고 생각했다.
그런데 조금만 곰곰이 생각해보면 이 방법은 치명적인 문제가 존재한다.
\(x_{i}\)값을 구하기 위해서 M개의 문자를 매번 읽어야 한다면, 이게 brute-force랑 뭐가 다르지?
그리고 해시 만드는 비용은? 이것도 무시할 수 없다.
하지만 당연하게도 이 부분에 대한 이야기도 이미 끝나있었다. ㅎ
🔬 관찰
- \(x_{i} = t_{i}R^{M-1} + t_{i+1}R^{M-2} + \dots + t_{i+M-1}R^{0}\)
- \(x_{i+1} = t_{i+1}R^{M-1} + t_{i+2}R^{M-2} + \dots + t_{i+M}R^{0}\)
생각해보면 M만큼 다 읽을 필요가 없다.
앞의 문자 해시값을 제거하고, 새로 읽을 해시값을 추가한다면 2번의 연산으로 해결할 수 있다.
💡 Rolling hash
✨ \(x_{i}\)를 이용하여 \(x_{i+1}\)을 쉽게 구하자!
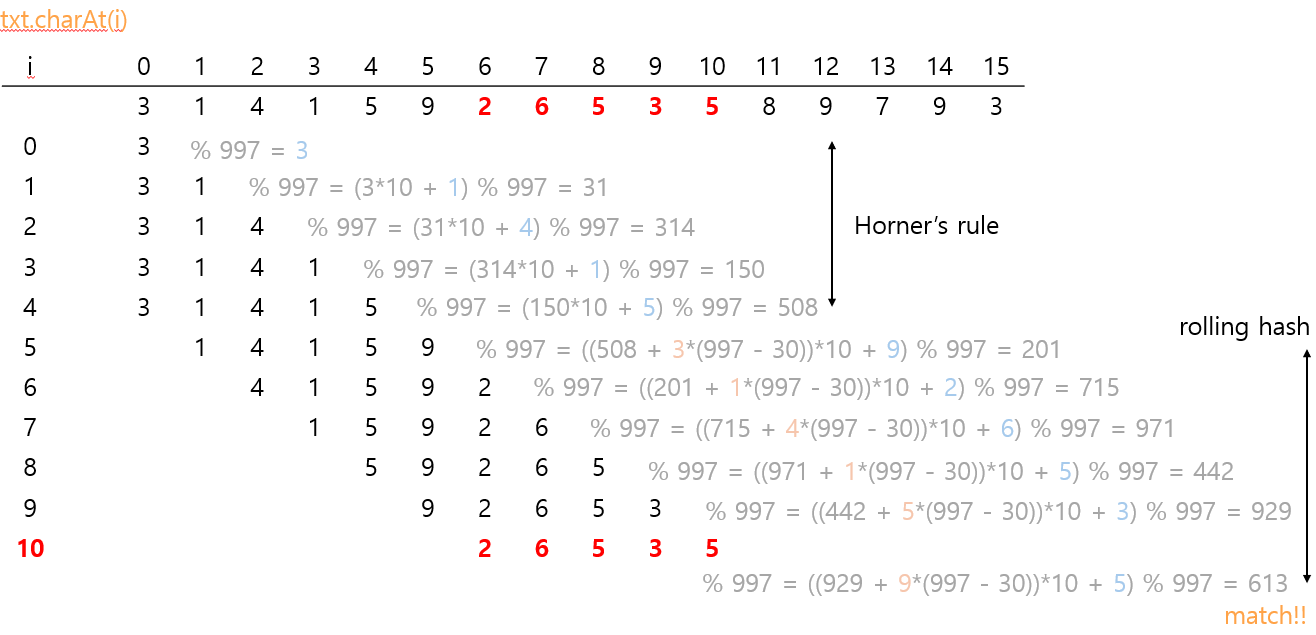
- 첫 번째 R개의 항들에 대해선 Horner의 방법을 사용한다.
- 나머지 항들은 Rolling hash를 사용한다. (오버플로우 방지를 위해 % 연산)
- \(x_{i+1} = (x_{i} - t_{i}R^{M-1})R + t_{i+M}R^{0}\)
- 효율성을 위해 \(R^{M-1}\)을 미리 캐싱해두는 것이 좋다.
- pattern이 5자이므로 M=5
- \(R^{M-1} = 10^{4} = 10000\) → \(10000 % 997 = 30\) → -30 % 997 = 997-30
🙄 -30 mod 997은 갑자기 왜 나와?
아오, 이것 때문에 탈모 걸리는 줄 알았네.
롤링 해시 공식이 \(x_{i+1} = (x_{i} - t_{i}R^{M-1})R + t_{i+M}R^{0} \)인데, \(R^{M-1} = 10^{4}\)임은 쉽게 알 수 있다.
문제는 이 값이 너무 크니까 modular 연산을 한 번 해주자.
그러면 10000 mod 997 = 30이 되는 것까지도 쉽게 알 수 있다.
그런데, 원래 공식상으로는 \(x_{i}-t_{i}R^{M-1}\)이 나올 차롄데, 여기서 - 부호를 제거해주기 위해서
\(-t_{i}R^{M-1}\)이 아니라, \(t_{i}(-R^{M-1})\)로 묶어버린다.
그럼 -30이네? modular 연산을 한 번 더 때림 ㅋㅋ
-30 mod 997을 하려니, 음수에 대한 나머지 연산이 되므로 \(-R^{M-1} = 997 - 30\)이 되는 것이다.
📌 구현
public class RabinKarp {
private final String pattern;
private final long patternHash;
private final int M, R = 256;
private final long Q;
private final long RM; // R^(M-1) % Q
public RabinKarp(String pattern) {
this.pattern = pattern;
this.M = pattern.length();
this.Q = BigInteger.probablePrime(31, ThreadLocalRandom.current()).longValue();
long tmp = 1;
for (int i = 1; i <= M-1; i++) {
tmp = (R * tmp) % Q;
}
RM = tmp;
patternHash = hash(pattern, M);
}
public int search(String txt) {
int N = txt.length();
if (N < M) return N;
long txtHash = hash(txt, M);
if (patternHash == txtHash && isSame(txt, 0)) return 0;
for (int i = M; i < N; i++) {
txtHash = (txtHash + Q - RM * txt.charAt(i - M) % Q) % Q;
txtHash = (txtHash * R + txt.charAt(i)) % Q;
if (patternHash == txtHash && isSame(txt, i - M + 1)) return i - M + 1;
}
return N; // Not Found
}
private long hash(String key, int M) { // key[0..M-1]의 해시값 계산
long h = 0;
for (int j = 0; j < M; j++) {
h = (R * h + key.charAt(j)) % Q;
}
return h;
}
private boolean isSame(String txt, int i) { // Las Vegas 방식
for (int j = 0; j < M; j++) {
if (pattern.charAt(j) != txt.charAt(i + j)) return false;
}
return true; // Monte Carlo 방식인 경우, true 반환
}
}