구종만님의 "프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략"을 기반으로 공부한 내용입니다.
📕 목차
1. 도입
2. 배열
3. 연결 리스트
4. 예제: 조세푸스 문제 (문제 ID: JOSEPHUS, 난이도: 하)
5. 큐와 스택, 데크
6. 예제: 짝이 맞지 않는 괄호 (문제 ID: BRACKETS2, 난이도: 하)
1. 도입
- def. 요소가 일렬로 나열되어 있는 자료 구조
- ex. 정적 배열, 동적 배열, 연결 리스트, 스택, 큐, 데크
✒️ Tip. 자료 구조에서의 시간 복잡도
| 자료 구조 | 접근 | 탐색 | 삽입 | 삭제 |
| 배열(array) | O(1) | O(N) | O(N) | O(N) |
| 스택(stack) | O(N) | O(N) | O(1) | O(1) |
| 큐(queue) | O(N) | O(N) | O(1) | O(1) |
| 이중 연결 리스트(doubly linked list) | O(N) | O(N) | O(1) | O(1) |
| 해시 테이블(hash table) | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리(BST) | O(logN) | O(logN) | O(logN) | O(logN) |
| AVL 트리 | O(logN) | O(logN) | O(logN) | O(logN) |
| 레드 블랙 트리 | O(logN) | O(logN) | O(logN) | O(logN) |
2. 배열
📌 정적 배열(static array)
- 같은 타입의 변수들로 이루어져 있다.
- 크기가 고정되어 있으며, 데이터들이 물리적으로 인접해있다. (공간지역성)
- 중복을 허용하고 순서가 존재한다.
- 랜덤 접근(random access)이 가능하여 원소를 빠르게 접근해야 하거나, 간단하게 데이터를 쌓고 싶을 때 사용한다.
- 순차 접근과 달리 인덱스에 해당하는 데이터에 접근할 수 있는 기능
📌 동적 배열(dynamic array)
- 정적 배열의 가장 큰 문제점인 선언 시점(컴파일 타임)에 크기를 지정해야 한다는 제약을 해결한다.
- 자료의 개수가 변함에 따라 크기가 변경된다.
- 중복을 허용하고 순서가 존재하며, 랜덤 접근이 가능하다. (정적 배열의 특징을 계승한다.)
- 탐색과 맨 뒤의 요소를 삭제하거나 삽입하는데 O(1)이 걸리지만, 맨 앞의 요소를 삭제하거나 삽입하는 데는 O(N)이 소요
- 배열의 크기를 변경하는 resize() 연산이 가능하며 O(N)이 소요.
- 언어 차원에서 지원되는 게 아닌 별도의 자료 구조이므로, 대개 언어 표준 라이브러리에서 지원한다. (ex. vector)
🤔 append()가 어떻게 O(1)에 해결되는가?
- 원소가 추가되면 배열은 resize() 연산을 통해 공간을 확보해야 하는데, 어떻게 append()는 O(1)로 해결이 될까?
- 동적 배열은 메모리를 할당받을 때, 배열의 크기가 커질 때를 대비하여 여유분의 메모리를 할당받는다.
- 만약 배열이 이미 할당한 메모리가 꽉 찬다면, 더 큰 메모리를 할당받아 원소를 모두 옮기는 식으로 동작한다.
- size: 배열 내 원소의 개수
- capacity: 실제 배열이 할당받은 크기
📌 동적 배열 재할당 전략
class DynamicArray {
int* data;
int capacity;
int size;
public:
...
void add(int value) {
if (size == capacity) {
// 용량을 10만큼 늘린다.
capacity += 10;
int* newData = new int[capacity];
// 데이터를 복사한다.
for (int i = 0; i < size; ++i) {
newData[i] = data[i];
}
if (data) delete[] data;
data = newData;
}
// 배열의 맨 뒤에 원소를 추가한다.
data[size++] = value;
}
};- 실제로 구현을 해보면 원소를 추가하기 위한 공간을 확보하기 위해 O(N+M)의 시간이 소요된다.
- 그렇다면 append() 연산을 여러번 하면 언젠가는 O(N)이 걸리는 때가 오지 않을까?
- append() 연산은 선형 시간이 맞지만, 해당 작업이 아주 가끔 발생한다면 전체 평균은 여전히 상수 시간이라 볼 수 있다.
✒️ 재할당 전략
- 용량을 늘리는 값의 기준인 M=100인 경우
- append() 연산이 1만 번 수행될 때, 99번 째마다 재할당이 발생한다.
- 복사 횟수는 100 + 200 + 300 + ⋯ + 9,900 = 495,000이므로, 크기 1만인 배열을 만드는 데 50만 번의 복사가 필요하다.
- M=1,000으로 늘린다면?
- 복사 횟수가 9번으로 줄어든다.
- 하지만 크기가 작은 원소 집합을 저장할 때 공간 낭비가 심각해진다.
- 사실 M의 크기는 상관이 없다.
- N번 append() 연산을 수행할 때, 재할당의 수는
- M이 상수이므로 N이 매우 크면 결국 K=O(N)이 된다.
- 재할당마다 복사하는 원소 수가 M, 2M, ⋯, K*M개로 증가하므로, 전체 복사하는 원소수는
- 따라서 N번 append() 연산 수행 결과가
- N번 append() 연산을 수행할 때, 재할당의 수는
- 할당 크기를 고정하지 않고 동적으로 변경하면 더 최적화할 수 있다.
- M을 고정하지 않고, 현재 가진 원소 개수에 비례하여 크기를 확장시키면 복사 총 횟수는 1 + 2 + 4 + ⋯ + 8,192 = 16,383
- i(i≥0)번 재할당 시 복사 원소수는
- 이걸 두 번 수행해도 O(N)이므로, append() 연산 한 번의 평균 시간은 O(1)이라 봐도 무방하다.
3. 연결 리스트
📌 정의

struct ListNode {
int element;
ListNode *prev, *next;
}- 데이터를 감싼 노드를 포인터로 연결해서 공간 효율성을 극대화 시킨 자료 구조
- 일반적인 배열은 임의의 위치에 원소를 삽입/삭제 하는 과정에서 해당 위치 뒤의 원소들을 하나씩 옮겨야 하므로 선형 시간이 소요된다.
- 메모리가 물리적으로 인접해있지 않고, 이전 혹은 다음 원소를 가리키는 포인터를 가지고 있다.
- 싱글 연결리스트: next 포인터만을 갖는다.
- 이중 연결리스트: next, prev 포인터를 갖는다.
- 원형 이중 연결 리스트: 마지막 노드의 next 포인터가 헤드 노드를 가리킨다.
- C++ STL의 list, 자바와 C#의 LinkedList가 해당된다.
📌 시간 복잡도
- 데이터가 물리적으로 인접해 있기 때문에 random access가 불가능하다. 따라서 탐색에 O(N)이 소요된다.
- 반면 새 노드를 삽입/삭제 시엔 포인터만 바꾸면 되므로 O(1)의 상수 시간으로 이루어진다.
📌 split

- 두 연결 리스트를 상수 시간에 합치는 작업이 매우 편리하다.
- 하지만 연결 리스트 크기를 O(1)에 알 수 없어진다.
- 일반적으로 원소 개수를 리스트 객체 내에 유지하면서 갱신한다.
- 하지만 잘라 붙이기 연산을 수행하면 몇 개의 원소가 추가될 지 알 수 없다.
- Java, C#에서는 split() 연산을 포기했고, C++은 지원은 하지만 리스트 크기를 구하기 위해 선형 시간을 소요한다.
📌 undo
// node 이전/이후 노드의 포인터를 바꾸어 node를 리스트에서 삭제
void deleteNode(ListNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
// node 이전/이후 노드의 포인터를 바꿔서 자기 자신을 다시 리스트에 삽입
void recoverNode(ListNode* node) {
node->prev->next = node;
node->next->prev = node;
}- 한 번 삭제했던 원소를 제자리에 쉽게 돌려놓을 수 있다.
- 하지만 이전/이후 노드가 삭제된 상태에서 수행하면 리스트가 망가지므로 언제나 삭제한 순서의 반대로 복구가 이루어질 때만 가능하다.
- 답의 조각을 만들어 상태를 갱신하고, 문제가 끝나면 다시 복구하는 조합 탐색 문제에서 유용하다.
📌 동적 배열 vs 연결 리스트
| 작업 | 동적 배열 | 연결 리스트 |
| 이전 원소/다음 원소 찾기 | O(1) | O(1) |
| 맨 뒤에 원소 추가/삭제하기 | O(1) | O(1) |
| 맨 뒤 이외의 위치에 원소 추가/삭제하기 | O(N) | O(1) |
| 임의의 위치의 원소 찾기 | O(1) | O(1) |
| 크기 구하기 | O(1) | O(N) 구현에 따라 O(1) |
- 삽입/삭제를 할 일이 없거나, 배열 끝에서만 하면 될 때는 동적 배열이 거의 항상 더 좋다. 공간 지역성의 원리로 인해 CPU 캐시 효율도 높여준다.
- 모든 원소를 순회하며 삽입/삭제가 빈번하다면 연결 리스트가 더 좋다.
4. 예제: 조세푸스 문제 (문제 ID: JOSEPHUS, 난이도: 하)
📌 문제
algospot.com :: JOSEPHUS
조세푸스 문제 문제 정보 문제 1세기에 살던 역사학자 조세푸스는 로마와의 전쟁에서 패해 N - 1명의 동료 병사들과 함께 출구가 없는 동굴에 포위당했다고 합니다. 동료 병사들은 로마에 항복하
algospot.com
아니, 죽은 병사들은 뭔...ㅋㅋ
📌 풀이
void josephus(int n, int k) {
// 리스트 준비
list<int> survivors;
for (int i = 1; i <= n; ++i) survivors.push_back(i);
// 죽을 사람을 가리키는 포인터
auto kill = survivors.begin();
while (n > 2) {
// 첫 번째 사람을 죽인다.
kill = survivors.erase(kill);
if (kill == survivors.end()) kill = survivors.begin();
--n;
// k-1명 건너뛴다.
for (int i = 0; i < k - 1; ++i) {
++kill;
if (kill == survivors.end()) kill = survivors.begin();
}
}
cout << survivors.front() << " " << survivors.back() << endl;
}- 원형 연결 리스트에서 죽을 사람을 가리키는 포인터 kill을 유지한다.
- 포인터가 사람을 죽이고 포인터를 K-1번 앞으로 옮기는 방식으로 진행된다.
- 한 사람이 죽을 때마다 포인터를 K-1번 옮기므로, 전체 시간 복잡도는 O(NK)가 소요된다.
- K가 너무 크다면 (K-1) mod N번 포인터를 옮겨, 시간 복잡도를
- 이 외에도 동적 계획법을 활용한 O(N) 풀이, 시뮬레이션을 한 번에 여러 단계 진행한 O(KlgN)의 알고리즘 등 다양한 방법이 있다.
5. 큐와 스택, 데크
📌 도입
- 언제나 특정한 순서로 넣고, 특정한 순서로만 꺼낼 수 있는 자료 구조
- 연결 리스트나 배열로 쉽게 구현 가능하지만 이름이 붙었기에 개발자 간에 의사 소통이 더 쉬워져서 사용한다.
- 아래 세 가지 자료구조 모두 push(), pop() 연산이 상수 시간 O(1)에 이루어져야 한다.
- 큐(queue)
- 선입선출(FIFO, First In First Out) 구조
- 한쪽 끝에서 자료를 넣고 반대 쪽 끝에서 자료를 꺼낼 수 있다.
- CPU 작업을 기다리는 프로세스, 스레드 행령, 네트워크 접속 대기 행렬, BFS, cache 등에 사용한다.
- 스택(stack)
- 후입선출(LIFO, Last In First Out) 구조
- 한쪽 끝에서만 자료를 넣고 뺄 수 있다.
- 전산학에서 광범위하게 사용되며, 컴퓨터 내부적으로 함수들의 문맥(context)을 관리할 때 사용한다.
- 덱(dequeue)
- 양쪽 끝에서 자료들을 넣고 뺄 수 있는 자료 구조
- dequeue로 stack과 queue 모두 구현 가능하다.
📌 구현
1️⃣ 연결 리스트를 통한 구현
- 양쪽 끝에서 추가/삭제 모두 상수 시간 내에 해결 가능하므로 모든 연산이 상수 시간이라는 요구 조건을 쉽게 충족시킨다.
- 다만 노드 할당/삭제, 순차 탐색을 하는 데 시간이 소모되므로 가장 효율적인 구현은 아니다.
2️⃣ 동적 배열을 이용한 구현
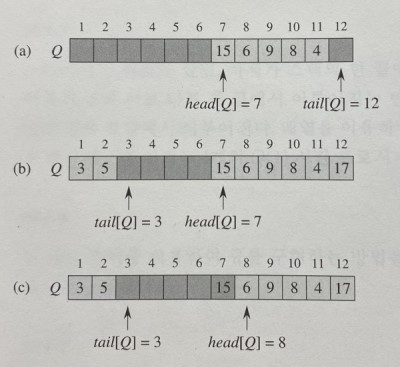
- stack의 경우엔 한쪽 끝에서만 삽입/삭제가 발생하므로 쉽게 구현할 수 있다.
- queue와 dequeue의 경우엔 앞에서 원소를 삽입/삭제하는 데 O(N)이 걸리므로 다른 방법이 필요하다.
- 첫 번째 원소(head)와 마지막 원소(tail)의 위치를 유지하면서 구현 가능하다.
- pop() 연산에 의해 head 앞 부분의 버려지는 공간을 재활용하고, push() 연산 시 공간이 없을 경우에만 재할당 과정을 수행한다면 공간을 효율적으로 활용할 수 있다.
- 동적 배열을 원형으로 만들었다고 볼 수 있기 때문에, 이러한 배열 구현을 환형 버퍼(circular buffer)라고 한다.
3️⃣ 표준 라이브러리
- 거의 모든 언어의 표준 라이브러리에서 구현체를 제공한다. (swift는 없더라. 깔깔)
- 이런 기초 자료 구조를 직접 구현하느라 시간 낭비 하지 말고, 특성과 사용법만 알아두고 적절히 사용할 줄 알면 된다.
📌 활용
🟡 조세푸스 문제 다시 풀기
- 죽을 사람을 가리키는 포인터를 옮기는 대신 사람들을 직접 움직이게 만들 수 있다.
- 그러면 다음 과정을 queue에 두 명이 남을 때까지 반복해서 해결 가능하다.
- queue의 첫 번째 사람이 나와서 죽고
- queue의 맨 앞에 있는 사람을 맨 뒤로 보내는 작업을 k-1번 반복한다.
- 알고리즘 수행 시간은 똑같지만, 구현이 보다 간단해진다.
🟡 울타리 자르기 문제 다시 풀기
[Algorithm Strategies] 3-7. 분할 정복
구종만님의 "프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략"을 기반으로 공부한 내용입니다. 📕 목차 1. 도입 2. 쿼드 트리 뒤집기 (문제 ID: QUADTREE, 난이도: 하) 3. 울타리 잘라내기 (문제 I
jaeseo0519.tistory.com
알고리즘 문제를 풀면서 생각해보아야 할 것들
이제 1년하고 1달 조금 넘게 코딩을 하면서, 알고리즘이라고는 실버 2주, 골드 1달, 플래티넘 1달 정도밖에 풀어보지 않은 짬밥에 뭘 얼마나 유용한 걸 설명할 수 있을 지는 모르겠지만 그래도 내
jaeseo0519.tistory.com
6. 예제: 짝이 맞지 않는 괄호 (문제 ID: BRACKETS2, 난이도: 하)
📌 문제
algospot.com :: BRACKETS2
Mismatched Brackets 문제 정보 문제 Best White is a mathematics graduate student at T1 University. Recently, he finished writing a paper and he decided to polish it. As he started to read it from the beginning, he realized that some of the formulas ha
algospot.com
- 전형적인 stack을 사용한 문제
📌 풀이
bool wellMatched(const string& formula) {
// 여는 괄호 문자들과 닫는 괄호 문자들
const string opening("({["), closing(")}]");
// 이미 열린 괄호들을 순서대로 담는 스택
stack<char> openStack;
for (int i = 0; i < formula.size(); ++i) {
// 여는 괄호인지 닫는 괄호인지 확인한다.
if (opening.find(formula[i]) != -1) {
// 여는 괄호라면 무조건 스택에 집어넣는다.
openStack.push(formula[i]);
} else {
// 이 외의 경우 스택 맨 위의 문자와 맞춰보자.
// 스택이 비어있는 경우에는 실패
if (openStack.empty()) return false;
// 서로 짝이 맞지 않아도 실패
if (opening.find(openStack.top()) != closing.find(formula[i])) return false;
// 짝을 맞추었으니 스택에서 열린 괄호를 뺀다.
openStack.pop();
}
}
// 닫히지 않은 괄호가 없어야 성공
return openStack.empty();
}- 이 문제의 재밌는 점은 닫힌 스택이 들어오자 마자 짝을 맞출 수 없으면 반드시 실패한다는 점이다.
- 백준에 괄호 관련 재밌는 문제가 많으니 풀어봐도 좋을 듯.