구종만님의 "프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략"을 기반으로 공부한 내용입니다.
📕 목차
1. 도입
2. 도시락 데우기 (문제 ID: LUNCHBOX, 난이도: 하)
3. 문자열 합치기 (문제 ID: STRJOIN, 난이도: 중)
4. 미나스 아노르 (문제 ID: MINASTIRITH, 난이도: 상)
1. 도입
• 탐욕적 알고리즘
• 예제: 회의실 예약
• 예제: 출전 순서 정하기 (문제 ID: MATCHORDER, 난이도: 하)
• 탐욕적 알고리즘 레시피
📌 탐욕법(Greedy Method)
완전 탐색과 동적 계획법 알고리즘과 동일하게 여러 개의 조각으로 쪼개고, 각 단계마다 답의 한 부분을 만들어간다.
하지만 결정적 차이는 모든 선택지를 고려하고 가장 좋은 답을 찾는 것이 아니라, 각 단계별로 지금 당장 가장 좋은 방법만을 선택하는 방법이다.
즉, 지금의 선택이 앞으로 남은 선택들에 어떤 영향을 끼칠 지는 관심 밖의 문제다.
예를 들어, 여행하는 외판원 문제를 동적 계획법으로 풀이하면 다음에 도착할 수 있는 도시들을 하나하나 검사해보고, 남은 도시들을 모두 순회하는 데 필요한 거리의 합을 최소화하는 답을 찾을 것이다. (3-9 내용인데, 내용이 너무 많고 어려워서 포스팅 순서가 바뀌는 바람에 아직 안 올렸다.)
하지만 탐욕법으로 풀이하면 다음과 같은 몇 가지 다른 방법들로 풀이할 수도 있다.
- 당장 다음 도시까지의 거리만을 최소화하여, 아직 방문하지 않은 도시 중 가장 가까운 도시로 움직이는 것을 모든 도시를 방문할 때까지 반복한다.
- 방문하지 않고 남은 도시들이 가능한 한 서로 모여 있도록 만든다.
- 다른 도시와 가장 멀리 떨어져 있는 도시를 먼저 가는 방식으로 구현한다.
여기까지만 보면, '정말 이런 방법으로 최적해를 구할 수가 있어?'라고 생각할 텐데 그럴 리가.
애석하게도 최적해를 찾지 못 하는 경우가 대부분이다.
💡 탐욕적 알고리즘을 사용하는 경우 2가지
• 탐욕법을 사용해도 항상 최적해를 구할 수 있는 문제를 만난 경우 (동적 계획법보다 수행 시간이 빠르다.)
• 시간·공간적 제약으로 인해 다른 방법으로 최적해를 찾기 너무 어려워서, 타협으로 적당한 근사값을 찾는 경우. (최적은 아니지만, 임의의 답보다는 좋은 답을 구하는 용도)
이 중에서도 프로그래밍 대회에선 첫 번째 용도로만 사용된다.
근사해를 찾는 문제는 거의 나오지 않을 뿐더러, 나온다 하더라도 11장의 조합 탐색, 메타휴리스틱 알고리즘들이 더 좋은 답을 주는 경우가 많기 때문이다.
탐욕법은 개념이 간단한 데에 비해, 최적해를 얻을 수 있는 접근이 직관적이지 않은 경우도 많기 때문에 알고리즘 정당성을 증명하는 과정이 필수적으로 선행되어야 한다.
📌 예제: 회의실 예약
🗒️ 문제
1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
하나밖에 없는 회의실을 n개의 팀이 사용하고 싶은 회의 시간을 공지했을 때,
하루에 최대한 많은 팀에게 회의실을 배정해줄 수 있을까?
✒️ 내 풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> pii;
int n;
vector<pii> teams;
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n;
for (int i=0; i<n; ++i) {
int start, end; cin >> start >> end;
teams.push_back({end, start});
}
sort(teams.begin(), teams.end());
int res = 0, lastEndTime = 0;
for (int i=0; i<n; ++i) {
int start = teams[i].second, end = teams[i].first;
if (lastEndTime <= start) {
lastEndTime = end;
++res;
}
}
cout << res << "\n";
return 0;
}동적 계획법으로 풀라고 하면 금방 풀었을 텐데, 탐욕법으로 풀이하려니 제법 골치 아팠다.
애초에 탐욕법에 대한 정의라곤 "현재 기준으로만 당장의 최적의 값을 찾아라" 정도밖에 몰랐던 터라,
이걸 곧이 곧대로 적용하려니 정당성 증명에서 도저히 해법이 나오질 않았다. (그래서 책의 증명 부분을 읽고, 코드를 작성해봤더니 똑같은 코드가 나오더라.)
이전에 유사한 문제들을 풀어본 짬밥이 있어서, 일단 'end를 기준으로 정렬해보면 어떻게 될까?'라는 의문이 우선 들었다.
즉, 가장 빨리 끝나는 회의들을 우선적으로 선별해보자는 심산이었다.
그런데 정렬을 하면서 end값이 동일한 케이스가 여러개면 start에 대해서 이차적으로 정렬을 해야 할 지 고민하던 와중에 '그럴 필요가 있을까?'를 가장 많이 고민했다.

예를 들어, start는 모두 다르지만 end는 모두 동일한 3개의 케이스가 존재한다고 가정하자.
end를 기준으로 정렬하면 위 세 가지 케이스는 순서가 뒤죽박죽이 될 수 있다.
그렇다면 회의 시간이 가장 짧은(start가 가장 느린) 2번 째 케이스를 우선적으로 정렬해야 한다고 생각할 수도 있다.
정답은 해도 되지만, 안 해도 된다는 것.

- 주황색이 선행 과정인 경우, 셋 중 무엇을 택해도 같은 결과를 보인다.
- 파란색 혹은 초록색이 선행 과정인 경우, 첫 번째 케이스는 선택될 수 없으므로 1번 문제로 돌아간다.
물론 위 두 가지 명제만으로는 정당성이 성립했다고 보기 어렵지만, 그냥 내가 증명할 수 있었던 최선만큼만 정리를 해둔 것이니, 자세한 내용은 책을 마저 리딩하는 것으로 하자.
🟡 무식하게 풀 수 있을까?
- 서로 겹치지 않는 회의들의 집합은 모두 이 문제의 답이라 할 수 있다.
- 그리고 그 중에서도 가장 큰 부분 집합이 최적해가 된다.
- 그러나 집합의 크기가 n이면, 부분 집합 수가 2^n이 되므로 n이 30만 되어도 시간 안에 문제를 해결할 수 없다.
🟡 탐욕적 알고리즘 구상
1️⃣ 길이가 짧은 회의부터 하나하나 순회하면서 겹치지 않는 것들을 찾아볼까?

- 그럴듯 하지만, 위의 케이스에서 두 개의 회의 대신 하나의 회의를 선택하게 된다.
2️⃣ 길이와 상관없이 가장 먼저 끝나는 회의부터 선택해볼까?
- 현재 시점에서 가장 먼저 끝나는 회의를 선택하고, 이 회의와 겹치는 다른 회의는 모두 배제하는 방식
- 목록 S에 남은 회의중 가장 일찍 끝나는 회의 \(s_{min}\)을 선택한다.
- \(s_{min}\)과 겹치는 회의를 S에서 모두 지운다.
- S가 텅 빌 때까지 반복한다.
- 과연 이 방법이 가능할까? 의문이 들면 이제 알고리즘 정당성 증명 단계로 넘어간다.
🟡 탐욕법의 정당성 증명
💡 탐욕적 알고리즘이 항상 최적해를 찾아낼 수 있다는 증명 패턴은 두 가지의 속성을 증명해야 한다.
• 탐욕적 선택 속성(Greedy Choice Property) : 모든 경우를 고려하지 않아도 언제나 최적해를 구할 수 있는가?
• 최적 부분 구조(Optimal Substructure) : 부분 문제의 치적해에서 전체 문제의 최적해를 만들 수 있는가?
- 탐욕적 선택 속성이 만족한다면, 각 단계의 탐욕적 선택이 '손해'를 볼 일이 없음을 의미한다.
- 위 문제의 경우 "가장 종료 시간이 빠른 회의(\(s_{min}\))를 포함하는 최적해가 반드시 존재한다."가 성립함을 보이면 된다.
- 탐욕적 선택 속성이 참이어도, 항상 최적의 선택만을 내려서 전체 문제의 최적해를 얻을 수 있음을 최적 부분 구조를 보여 증명해야 한다.
🟡 탐욕적 선택 속성
- S의 최적해 중에 \(s_{min}\)을 포함하지 않는 답이 있다고 가정하자.
- 서로 겹치지 않은 회의 목록에서 첫 번째로 개최되는 회의를 지우고 \(s_{min}\)을 추가해서 새로운 목록을 만들어 본다.
- \(s_{min}\)은 S에서 가장 일찍 끝나는 회의이므로, 지워진 회의는 \(s_{min}\)보다 일찍 끝날 수 없다.
- 두 번째 회의와 \(s_{min}\)이 겹치는 일은 존재하지 않으므로, 새로 만든 목록도 최적해 중 하나가 된다.
- 따라서 항상 \(s_{min}\)을 포함하는 최적해가 존재한다.
🟡 최적 부분 구조
- 대개 매우 자명해서 따로 증명할 필요가 없는 경우가 대부분이지만, 첫 번째 선택을 하고 나서 남는 부분 문제는 최적이 아닌 방법으로 풀어야 할 때 성립하지 않는다.
- 이 문제의 경우는 첫 번째 회의를 선택하고 겹치는 회의를 모두 걸러내면, 남은 회의 중 당연히 최대한 많은 회의를 선택해야 하므로 정당성이 성립한다.
🟡 구현
// 코드 10.1 회의실 예약 문제를 해결하는 탐욕적 알고리즘
// 각 회의는 [begin, end) 구간 동안 회의실을 사용한다.
int n;
int begin[100], end[100];
int schedule() {
// 일찍 끝나는 순서대로 정렬한다
vector<pair<int, int> > order;
for (int i = 0; i < n; ++i)
order.push_back(make_pair(end[i], begin[i]));
sort(order.begin(), order.end());
// earliest: 다음 회의가 시작할 수 있는 가장 빠른 시간
// selected: 지금까지 선택한 회의의 수
int earliest = 0, selected = 0;
for (int i = 0; i < order.size(); ++i) {
int meetingBegin = order[i].second, meetingEnd = order[i].first;
if (earliest <= meetingBegin) {
// earliest를 마지막 회의가 끝난 시간 이후로 갱신하고
// 선택된 회의에 추가한다
earliest = meetingEnd;
++selected;
}
}
return selected;
}- 모든 회의 목록을 저장하고 모든 회의를 종료 시간의 오름차순으로 정렬한다.
- 정렬을 하지 않으면, 배열에 회의 목록을 "저장"하고 겹치는 회의를 "제거"해야 하는데, 매번 조회를 하기 위해 O(N^2)의 시간 복잡도가 나온다.
- 정렬된 배열의 첫 번째 회의는 무조건 선택해도 되며, 겹치는 회의를 지울 필요가 없다.
- 앞서 증명한 내용에 따라, 가장 빠른 종료 시간을 가진 회의 \(s_{min}\)을 포함하는 최적해가 언제나 존재하기 때문이다.
이렇게 하면, 정렬 시간인 O(NlgN)이 알고리즘의 전체 시간 복잡도가 된다.
🧐 난 동적 계획법으로 풀었는데?
- 마찬가지로 회의들을 끝나는 시간이 증가하는 순으로 정렬해본다.
- \(schedule(idx) = meeting[idx]\) 혹은 그 이전에 끝나는 회의들 중 선택할 수 있는 최대 회의의 수
- schedule()이 매 단계에서 meeting[idx]를 "선택할 거냐, 말 거냐"의 여부를 판가름 한다.
- idx번 회의가 시작하기 전에 끝나느 회의들 중 마지막 회의 번호를 before[idx]에 저장했다면, 다음 두 가지로 재귀를 호출할 수 있다.
- 현재 회의를 선택하지 않은 경우: schedule(idx-1)
- 현재 회의를 선택한 경우 : 1 + schedule(before[idx])
- before[]을 만드는 데 O(nlgn), schedule() 수행에 2O(n)의 시간이 걸리니 탐욕법과 동일한 시간 복잡도를 가진다.
코드로 나타내면 아래와 같을 것이다. (틀렸을 수도..? 혹시 오류 발견하신 분은 댓글 부탁드립니다.)
vector<pair<int, int>> meeting; // 회의들이 끝나는 시간이 증가하는 순으로 정렬
int before[100]; // idx번 회의가 시작하기 전에 끝나는 회의들 중 마지막 회의 번호
int cache[100]; // -1로 초기화
int schedule_dp(int idx) {
if (idx == -1)
return 0;
int& ret = cache[idx];
if (ret != -1)
return ret;
return ret = max(schedule_dp(idx - 1), schedule_dp(before[idx]) + 1);
}- 당연히 지금 한 단계만을 고려한 탐욕법으로 해결할 수 있다는 말은, 모든 단계를 고려하는 동적 계획법으로도 풀 수 있음을 의미한다.
- 다만, 동적 계획법에 필요한 메모리나 시간이 과도하게 큰 경우 동적 계획법으로 해결할 수 없는 경우에 탐욕법을 사용한다.
📌 예제: 출전 순서 정하기 (문제 ID: MATCHORDER, 난이도: 하)
🗒️ 문제
algospot.com :: MATCHORDER
출전 순서 정하기 문제 정보 문제 전세계 최대의 프로그래밍 대회 알고스팟 컵의 결승전이 이틀 앞으로 다가왔습니다. 각 팀은 n명씩의 프로 코더들로 구성되어 있으며, 결승전에서는 각 선수가
algospot.com
완전 탐색으로 해결하는 방식은 오히려 떠오르질 않고,
동적 계획법으로 푼다면 경기에 출전시킨 한국 선수를 방문 처리하여, 가장 최적의 결과를 구할 수 있을 것이다.
탐욕법으로 접근한다면, 레이팅이 너무 높은 선수에겐 가장 약한 전력을 내어 점수를 따내는 방식이 될 것 같다.
🟡 무식하게 풀 수 있을까?
- n명의 선수가 있으므로 n!개의 답이 존재한다. (러시아 선수는 냅두고, 한국 선수 배치만 바꿔보면 된다.)
- 당연히 타임 오버가 날 것이므로 패스
🟡 그렇다면 동적 계획법은 어떨까?
- order(taken) = 각 한국팀 선수를 이미 순서에 추가했는지 여부가 taken에 주어질 때, 남은 선수들을 적절히 배치해서 얻을 수 있는 최대 승수
- 재귀의 깊이로 현재 상대할 러시아 선수를 판단하고, 아직 출전시키지 않은 선수들을 차례로 배치해서 최대 승수를 얻을 수 있는 경우를 판단해보면 된다.
아니, 근데 이 방법이 왜 O(N*2^N)이 나옴...?
고민하다가 시간이 너무 빼앗겨서 멈췄는데, 다 정리하고 다시 봐야겠다.
🟡 탐욕적 알고리즘 구상
- 상대 선수를 이길 수 있는 한국 선수가 있다면, 그 중에서도 가장 낮은 선수를 상대방 선수와 경기 시킨다.
- 상대방 선수가 한국팀 모든 선수보다 레이팅이 높다면, 남은 선수 중 가장 레이팅이 낮은 선수를 보낸다. (버림수)
참고로 이 문제를 해결하는 탐욕적 알고리즘은 여러 가지가 있고, 현재 설명하는 방식은 그 중 한 가지 사례에 불과하다.
🟡 탐욕적 선택 속성 증명
| 러시아 | ⋯ | 999,999,999 | ⋯ | x | ⋯ | 1,900 |
| 한국 | ⋯ | B | ⋯ | A | ⋯ | 2,000 |
- 각 경기에 대해 이 경기를 질 수밖에 없는 경우, 이길 수 있는 경우로 나누어 선택이 옳음을 보이면 된다.
- 레이팅이 가장 낮은 선수 A 대신 B를 보내는 경우 (A < B < 999,999,999)
- A와 B의 순서를 바꾸어도 어차피 지겠지만, 적어도 A를 상대하던 x는 레이팅이 더 높은 선수를 상대하게 된다.
- 따라서 승수가 줄지 않으면서, 이 경기에 A를 내보내는 최적해가 존재한다.
| 러시아 | ⋯ | 2,000 | ⋯ | x | ⋯ | 1,900 |
| 한국 | ⋯ | B | ⋯ | A | ⋯ | 2,000 |
- 레이팅이 가장 낮은 선수 A 대신 B를 내보내는 경우 (B > A >= 2,000)
- 어차피 이길 승부이면서, x는 더 레이팅이 높은 선수를 상대해야 하므로 이 순서 또한 최적해가 성립한다.
- 만약, A 대신 C(< 2,000) 선수를 대신 출전시킨 최적해가 존재한다면?
- 해당 경기는 이길 수 있으나 지는 경기가 된다. (A 대신 지는 경기)
- A와 바꾼다 하더라도 A는 이기고(승수 +1), C는 질 테니(승수 -1) 여전히 최적해가 성립한다.
✒️ 탐욕적 선택 속성을 증명하는 패턴
① 우리가 선택한 방법을 포함하지 않는 최적해의 존재를 가정한다.
② 적절히 조작하여 우리가 선택한 방법을 포함하는 최적해를 만들어 낸다.
③ ②를 통해 항상 우리가 선택한 방법을 포함하는 최적해가 있음을 증명한다.
아...어렵다. 아직 써먹긴 모호함.
🟡 최적 부분 구조 증명
- 첫 번째 경기에 나갈 선수를 선택하고 나면 남은 선수들을 경기에 배정하는 부분 문제가 파생된다.
- 남은 경기 또한 최다승을 얻는 것이 좋으니 최적 부분 구조도 자명하다.
🟡 구현
// 코드 10.2 출전 순서 정하기 문제를 해결하는 탐욕적 알고리즘
int order(const vector<int>& russian, const vector<int>& korean) {
int n = russian.size(), wins = 0;
// 아직 남아 있는 선수들의 레이팅
multiset<int> ratings(korean.begin(), korean.end());
for (int rus = 0; rus < n; ++rus) {
// 가장 레이팅이 높은 한국 선수가 이길 수 없는 경우
if (*ratings.rbegin() < russian[rus])
ratings.erase(ratings.begin());
// 이 외의 경우 이길 수 있는 선수 중 가장 레이팅이 낮은 선수를 이긴다
else {
ratings.erase(ratings.lower_bound(russian[rus]));
++wins;
}
}
return wins;
}multiset을 처음 봐서 찾아보니 "중복을 허용하는 set"이라고 보면 된다.
레이팅 점수가 같은 한국 선수들을 set 자료형에 중복을 허용하여 담아서 자동으로 정렬시킬 때 쓸 수 있다.
- rbegin() : multiset에서 가장 큰 값(오른쪽)을 찾는 메서드
- lower_bound() : multiset은 중복을 허용하므로 `russian[rus]`이 가리키는 값 중 처음을 가리킨다.
- upper_bound()는 중복 값의 끝을 가리키는데 {40, 40, 40, 50}이 저장되어 있으면, 50을 가리키고 있다.
- lower_bound의 인자 k와 동일한 값이 없다면, ratings 내에서 k보다 큰 값 중 가장 작은 값을 선택한다.
📌 탐욕적 알고리즘 레시피
- 문제의 답을 만드는 과정을 여러 조각으로 나눈다. (부분 문제로 나누는 것은 동적 계획법과 동일)
- 각 조각마다 어떤 우선 순위로 선택할지 결정한다.
- 이에 대한 직관을 얻고 싶다면 예제 입력이나, 작은 입력을 몇 개 손으로 풀어보는 것이 좋다.
- 어떤 방식이 동작할 것 같다면 두 가지 속성을 증명하라.
- 탐욕적 선택 속성
- 항상 각 단계에서 우리가 선택한 답을 포함하는 최적해가 존재함을 보여라.
- 대부분 우리가 선택한 답과 다른 최적해가 존재함을 가정하고, 이것을 조작했을 때 우리가 선택한 답을 포함하는 최적해로 바꿀 수 있는 형태가 된다.
- 최적 부분 구조
- 각 단계에서 항상 최적의 선택만을 했을 때 전체 최적해를 구할 수 있는지 여부를 증명하라.
- 대부분은 이 속성이 성립하는지는 쉽게 알 수 있다. (일부분만 탐욕적이고, 나머지는 그게 아닌 경우는 쓰면 안 된다.)
- 탐욕적 선택 속성
2. 도시락 데우기 (문제 ID: LUNCHBOX, 난이도: 하)
📌 문제
algospot.com :: LUNCHBOX
Microwaving Lunch Boxes 문제 정보 문제 After suffering from the deficit in summer camp, Ainu7 decided to supply lunch boxes instead of eating outside for Algospot.com winter camp. He contacted the famous packed lunch company "Doosot" to prepare N lun
algospot.com
- n개의 도시락을 주문함(도시락은 여러 종류)
- 전자레인지가 하나밖에 없는데, 한 번에 한 개의 도시락밖에 데울 수 없다.
- i번째 도시락을 데우는 데 \(m_{i}\)초가 걸리고, 먹는데 \(e_{i}\)초가 걸린다.
- 도시락은 두 번에 나누어 데울 수 없으며, 각 사람은 자기 도시락을 다 데우는 대로 다른 사람들을 기다리지 않고 먹기 시작한다.
- 이 때, N명의 인원이 모두 점심을 먹는 데 걸리는 최소 시간을 구하라.
📌 최소화해야 할 값
한 사람에게 소요되는 시간은 (도시락 데우는 시간 + 도시락을 먹는 시간)이고, 그 중에서도 가장 늦게 먹는 사람에 대한 시간을 최소화하는 것이 중요하다.
$$ \overset{n-1}{\underset{i=0}{max}}(e_{p[i]}+\sum_{j=0}^{i}m_{p[j]}) $$
(단, P는 {0, 1, 2, ⋯, n-1}의 순열로 각 도시락을 데우는 순서를 의미한다.)
📌 탐욕적 선택 속성 증명
- (데우는 시간 + 먹는 시간)이므로 먹는 시간이 끝나는 기준으로 최적화 접근이 가능하다.
- 나는 데우는 시간, 먹는 시간을 따로 두고 접근해야 한다고 생각했는데 어차피 데우자마자 먹기 시작한다고 했으니 그렇게까지 복잡하게 생각할 필요가 없었다.
- 설령 m = [10000, 1], e = [1, 100]이어도 데우는 시간은 고정이므로 10000분 짜리를 먼저 데우는 것보다, 100분동안 먹더라도 데우는 데 1분짜리인 것을 고르는 것이 낫다.
| 번호 | 0 | ⋯ | x | x+1 | ⋯ | n-1 |
| 도시락 | A | ⋯ | B | ⋯ | ⋯ | ⋯ |
- 먹는 데 가장 오래 걸리는 B를 먼저 데우는 최적해가 반드시 하나는 존재함을 보이면 된다.
- A를 먼저 데우는 최적해가 존재한다고 가정한다.
- A와 B의 위치를 바꾸었을 때도 최적해가 성립함을 보이면 된다.
- A와 B를 바꾸어도 x+1번 이후 도시락이 기다려야 하는 시간은 같으므로, 0~x번 도시락들만 고려해도 무방하다.
- 이 때, 0~x번까지 도시락을 데우는 시간 + B를 다 먹는데까지 걸리는 시간의 합은 \(max = e_{p[x]}+\sum_{i=0}^{x}m_{p[i]}\)
- 0~x번 순서를 아무리 바꾸어도 max값을 초과할 수 없다. (B는 가장 늦게 데우는데, 먹는 시간도 가장 오래 걸렸으므로)
- 이렇게 되면, 0~x 사이의 임의의 y번 째 도시락을 먹는데 걸리는 시간은 \(max = e_{p[y]}+\sum_{i=0}^{y}m_{p[i]}\)
- y번째 도시락은 \(e_{p[x]} \geq e_{p[y]}\)와 \(\sum_{i=0}^{x}m_{p[i]} \geq \sum_{i=0}^{y}m_{p[i]}\) 모두 성립한다. (먹는 데 더 오래 걸리지도, 더 오래 기다려야 하는 것도 아니기 때문)
- 즉, y번째 도시락을 먹는 데 걸리는 시간은 max보다 클 수 없다.
- 따라서 A와 B의 순서를 서로 바꾼 답이 최적해보다 나빠질 수 없으므로, 이 답도 최적해가 성립한다.
📌 최적 부분 구조 증명
이 경우에도 0~x번 째 도시락의 우선 순위를 정했다면, 남은 도시락에 대해서도 가장 늦게 다 먹는 시간을 최소화해서 손해볼 일이 없으므로 성립한다.
📌 구현
// 코드 10.3 도시락 데우기 문제를 해결하는 탐욕적 알고리즘
int n, e[MAX_N], m[MAX_N];
int heat() {
// 어느 순서로 데워야 할지를 정한다.
vector<pair<int, int>> order;
for (int i = 0; i < n; ++i)
order.push_back(make_pair(-e[i], i));
sort(order.begin(), order.end());
// 해당 순서대로 데워먹는 과정을 시뮬레이션한다.
int ret = 0, beginEat = 0;
for (int i = 0; i < n; ++i) {
// 데우는 시간과 먹는 시간을 더한다.
int box = order[i].second;
beginEat += m[box];
ret = max(ret, beginEat + e[box]);
}
return ret;
}- 먹는 시간이 작은 순으로 정렬하기 위해 compare 함수를 재정의해도 되지만, 먹는 시간의 부호를 뒤집어서 역순 정렬을 보다 간단하게 구현할 수 있다.
- `ret = beginEat + e[box]`가 아닌, `max(ret, begin + e[box])`를 하는 이유가 의아했는데 당연한 거였다.
- e = [10, 1, 2], m = [2, 1, 1]이면, e가 10,2,1(m은 2,1,1) 순으로 들어갈 텐데 `ret = beginEat + e[box]`로 계산하면, `(2+10) + (1+1) + (1+2)`가 된다.
- 어차피 첫 도시락을 다 데우고 먹는데 12분이 걸리므로, (1+1) + (1+2)는 포함돼선 안 된다.
3. 문자열 합치기 (문제 ID: STRJOIN, 난이도: 중)
📌 문제
algospot.com :: STRJOIN
문자열 합치기 문제 정보 문제 프로그래밍 언어 C 의 큰 문제점 중 하나는 언어 차원에서 문자열 변수형을 지원하지 않는다는 것입니다. C 에서는 문자 배열로 문자열을 표현하되 \0 (NULL) 로 문자
algospot.com
C언어로 문자열 다루는 건 42Seoul에서 너무 지긋지긋하게 봤더니 문제에 공감해버렸다.
문제 접근은 혹시나 해서 가장 작은 수끼리 더해서 합을 만들고, 새로운 수열에서 다시 가장 작은 수끼리 합을 더하는 방식으로 접근하니 답이 나왔다. (그래서 이걸 어떻게 구현하라고?)
📌 탐욕적 알고리즘의 구상
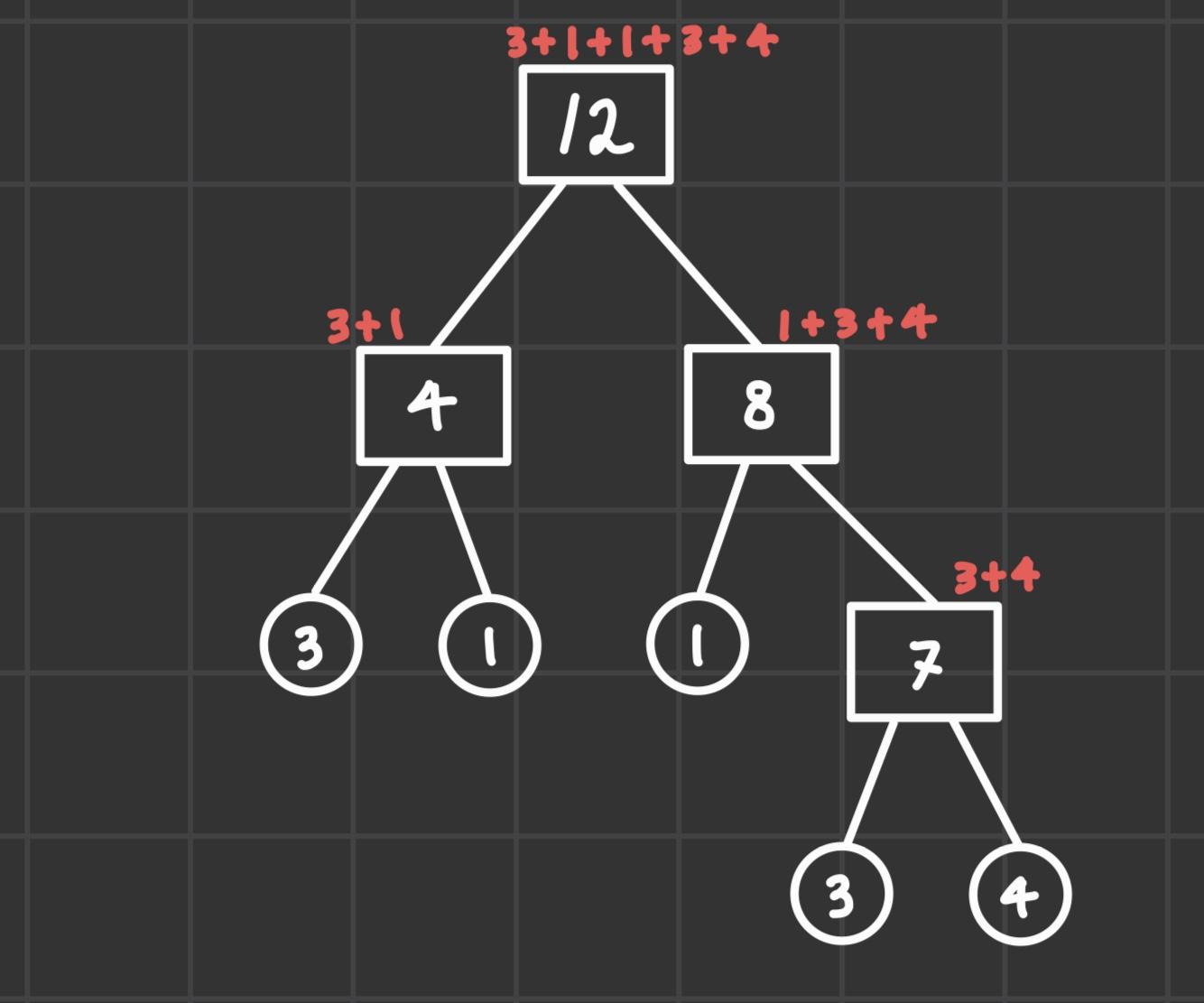
문자열을 합치는 비용은 Bottom-up 방식으로 이루어지는 것을 알 수 있다.
위의 방식대로 조합하면 비용은 총 31(=7+4+8+12)이 되는데, 각 조합수들을 쪼개보면 하나의 문자열로 인해 발생하는 총 비용은 이 문자열이 병합되는 횟수 * 문자열의 길이가 된다.
(예를 들어, 4의 길이를 가진 문자열은 3번 사용되므로 12(=4*3)만큼의 비용을 차지한다.)
여기서 직관력을 발휘하면 한 가지 가정을 세워볼 수 있다.
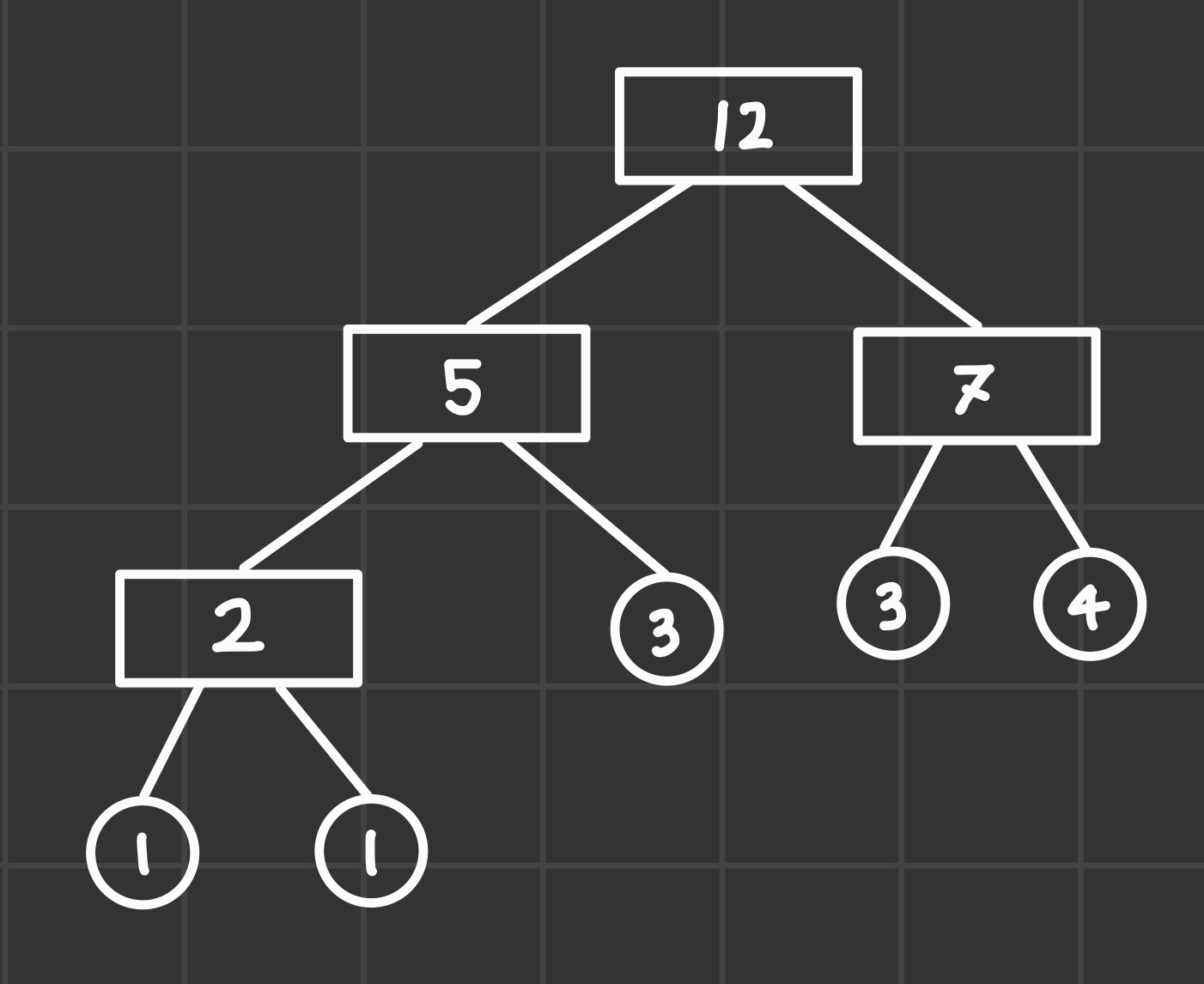
문자열이 길 수록(비용이 클 수록) 연산이 덜 들어가는 게 좋으니, 트리의 위쪽으로 올리는 것이 좋을 것이다.
그렇게 하기 위해선 "항상 가장 짧은 두 개의 문자열을 합치도록 한다"라는 가정을 증명해보면 된다.
📌 정당성 증명
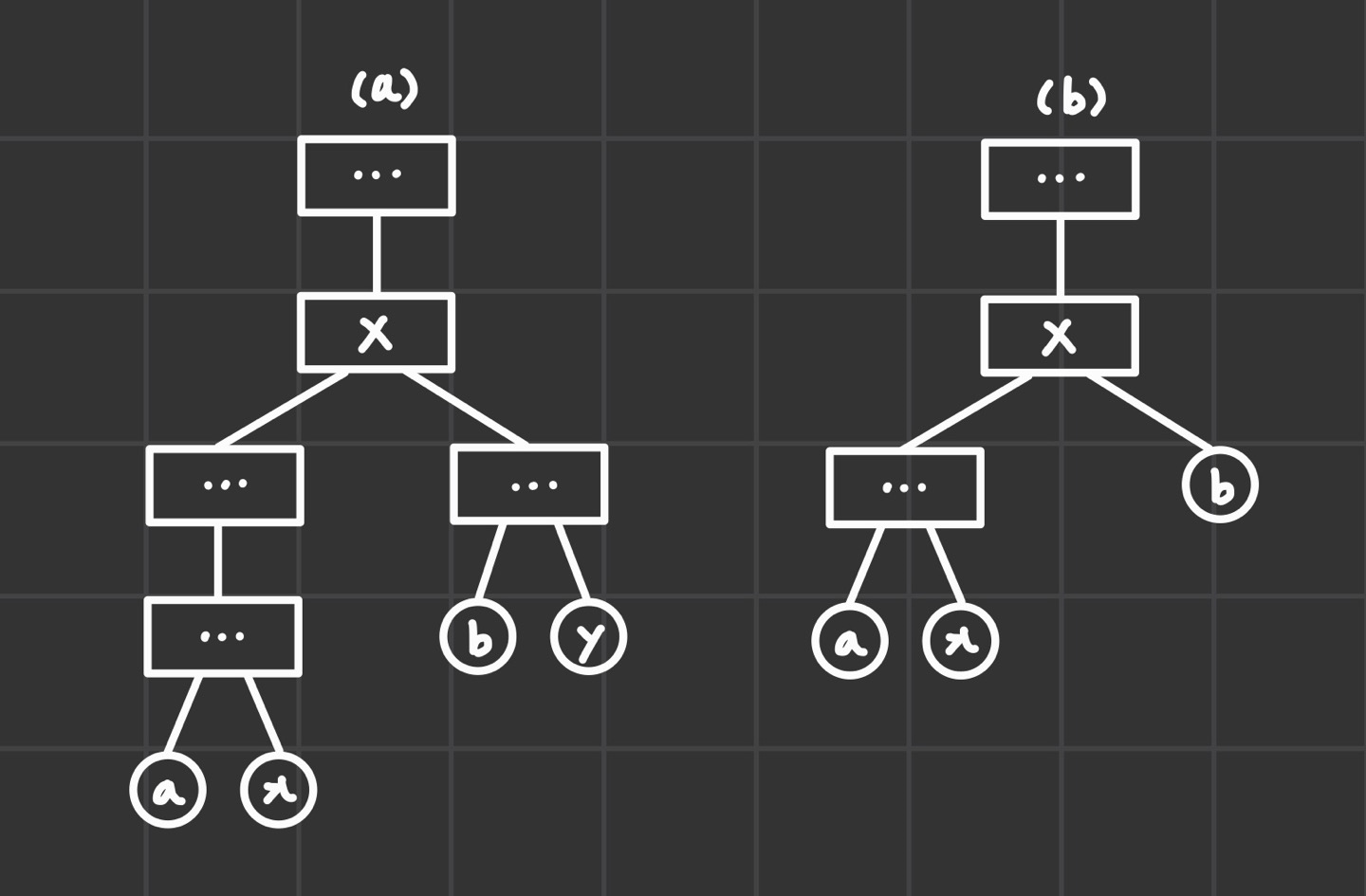
이전까지 했듯이, 매 단계마다 가장 짧은 두 문자열을 합치는 선택을 포함하는 최적해가 반드시 존재함을 보이면 된다.
- 가장 짧은 문자열 a, b를 처음에 붙이지 않은 상황을 가정한다. ((a)나 (b)의 상황, X는 a,b가 최초로 합쳐지는 문자열)
- X의 길이 자체는 일정하므로, 기저 사례의 문자열의 위치가 바뀌어도 X 윗부분은 변하지 않는다. (따라서 X 아래만 고려)
- a, b가 X에서 몇 단계가 떨어져 있는지 비교
- 거리가 같은 경우
- x와 b의 위치를 서로 바꾸어도 답은 같다.
- 거리가 다른 경우
- a,b 중 X보다 가까운 쪽을 더 먼 쪽으로 옮긴다. (위 예시에선 b와 x의 위치를 바꾼다.)
- x의 길이는 언제나 b보다 크므로, x의 병합 횟수가 줄어들게 하는 것이 항상 이득이거나 같은 비용이 든다.
- 거리가 같은 경우
- 두 문자열을 합치고 남은 문자열들도 항상 최소 비용을 써서 합쳐야 하므로 최적 부분 구조는 자명하다.
📌 구현
// 코드 10.4 문자열 합치기 문제를 해결하는 탐욕적 알고리즘
// 문자열들의 길이가 주어질 때 하나로 합치는 최소 비용을 반환한다.
int concat(const vector<int>& lengths) {
// 비교 함수를 greater<>로 선언해 최소 힙을 만든다
priority_queue<int, vector<int>, greater<int>> pq;
for (int i = 0; i < lengths.size(); ++i)
pq.push(lengths[i]);
int ret = 0;
// 힙에 원소가 하나만 남을 때까지
while (pq.size() > 1) {
// 가장 짧은 문자열 두 개를 찾아서 합치고 큐에 넣는다
int min1 = pq.top(); pq.pop();
int min2 = pq.top(); pq.pop();
pq.push(min1 + min2);
ret += min1 + min2;
}
return ret;
}최소힙..오랜만에 봐서 살짝 당황스러웠지만, 그리 어려운 내용은 아니다.
[Python] 1927 - 최소 힙 (실버2) : 최소 힙
1. 문제 설명 https://www.acmicpc.net/problem/1927 1927번: 최소 힙 첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연
jaeseo0519.tistory.com
언제나 가장 작은 값이 root에 위치해 있기 때문에, 값을 두 개 꺼내고 더해서 넣음을 반복함으로써 길이가 1이 되면 최종 문자열이 만들어졌다고 판단하여 결과를 돌려주면 된다.
그나저나 최소힙 갑자기 구현 방식이 가물가물하다. 오랜만에 다시 해봐야 할 것 같다.
📌 이론적 배경: 허프만 코드
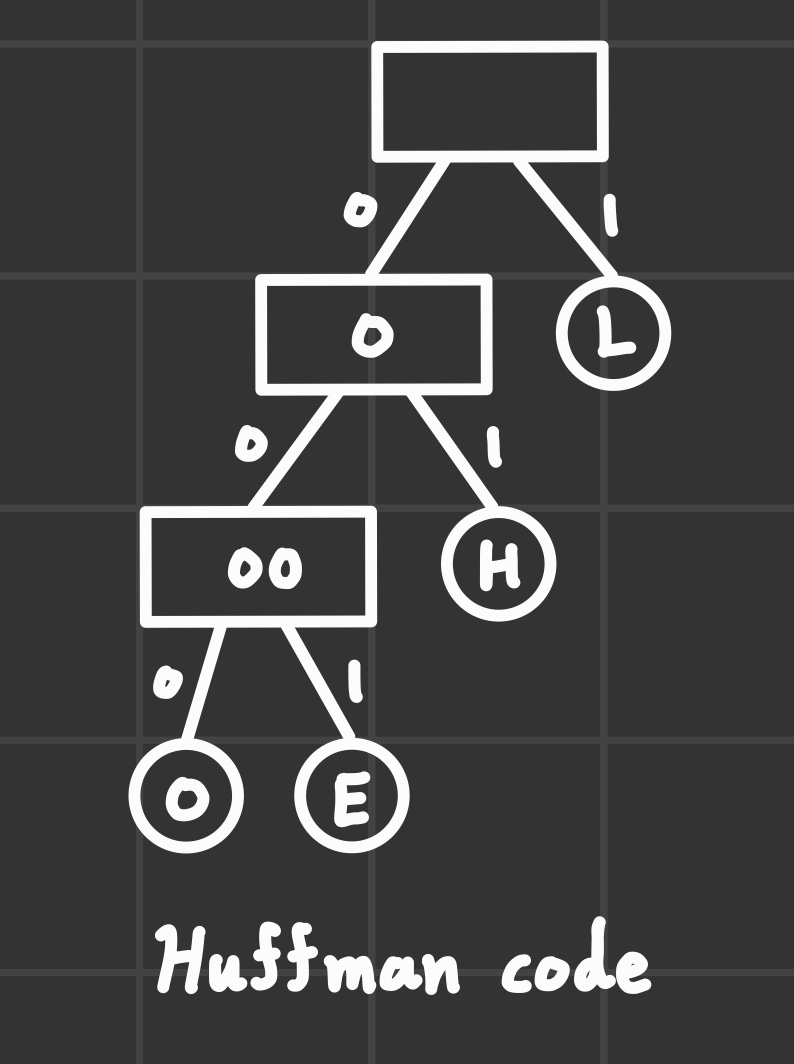
- 탐욕적 알고리즘의 유명한 예
- 가변 길이 인코딩(variable-length encoding) 테이블을 만드는 방법 (압축 알고리즘에 사용된다.)
- 원문의 각 글자를 서로 길이가 다를 수 있는 비트 패턴으로 바꾸어 원문의 길이를 줄이는 방법
- H(01₂), E(001₂), L(1₂), O(000₂) 이런 식으로 코드를 정한다면, HELLO를 0100111000₂로 압축하는 것
- 자주 출현하는 글자는 더 짧은 패턴으로 만드는 것이 유리하다.
- 허프만 코드는 원문에 출현하는 글자 출현 빈도에 따라 예상 길이를 최소화하는 비트 패턴을 만들어준다.
- 각 글자를 나타내는 인코딩은 내려가면서 만나는 간선들의 번호를 붙인 값이 된다.
- 따라서 각 글자에 대해 출현 확률과 코드의 길이를 곱한 것의 합을 최소화해야 한다.
4. 미나스 아노르 (문제 ID: MINASTIRITH, 난이도: 상)
📌 문제
algospot.com :: MINASTIRITH
미나스 아노르 문제 정보 문제 단 한 번도 함락된 적이 없다는 성채도시 미나스 아노르에는 반지름이 8 킬로미터나 되는 거대한 원형 성벽, 람마스 에코르가 있습니다. 도시 전체를 감싸는 이 거
algospot.com
아..풀려면 풀 수 있을 거 같은데, 풀기 싫게 생긴 문제.
이런 문제는 보통 기하 형태로 정직하게 풀려고 하기 보단 형태를 바꾸는 것이 좋더라.
특히나, 지금처럼 탐욕법을 쓰면 되겠다는 게 명확한 상황에선 더더욱 적절한 선택일 수도 있다.
원으로 둘러친 성벽을 직선으로 펼쳐버리고, 각 초소에서 측정가능한 성벽의 감시 범위를 따내면 될 것 같다.
근데 그걸 어떻게 하냐고? 밑에서 나온다..^^
참고로 기하+실수 좌표 문제 때문에 상당히 걱정스러울 수 있지만, 조건에서 "입력에 주어지는 실수가 아주 조금씩 늘어나거나 줄어들어도 답이 변하지 않는다"고 명시하고 있다.
즉, 수치적으로 안정된 입력값만 줄 거니까 실수 연산 오차로 인해서 틀릴 일은 없을 거라는 거니까 걱정을 조금 덜 수 있을 것이다.
📌 중심각 구간으로 원을 덮는 문제
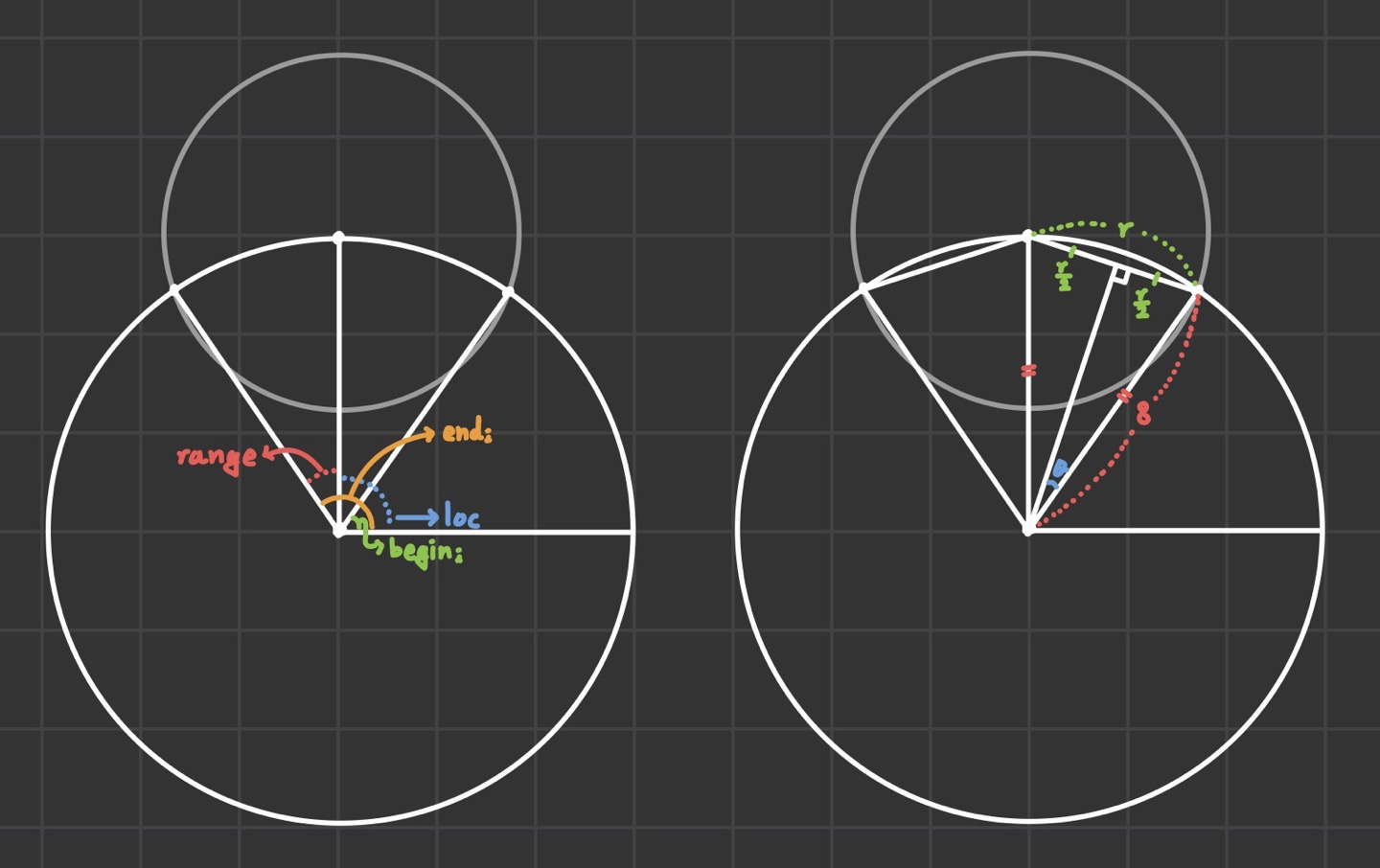
- 우선, 초소가 감시할 수 있는 성벽의 호의 구간[begin, end]을 구해야 한다.
- \(tan(loc) = \frac{y}{x}\)이므로, \(loc = arctan(y/x)\)가 된다.
- 점 P=(y,x)를 입력받으면, x축 양의 방향과 선분 \(\overline{OP}\) 사이 각도를 [-π, π] 구간 내의 값으로 반환하면 된다.
- range(성벽이 감시할 수 있는 범위)는 \(\theta = asin(\frac{r}{2}\times \frac{1}{8})\)를 이용하면, \(range = 2\theta = 2\times asin(\frac{r}{16})\)라는 것을 알 수 있다.
- begin과 end는 loc ± range로 쉽게 구할 수 있다.
- 전체 원을 감시할 수 있는지에 대한 여부는 감시 영역의 합집합이 [0, 2π]를 완전히 덮는지 판단해 알 수 있다.
// 코드 10.5 미나스 아노르 문제의 원들을 중심각의 구간으로 바꾸기
const double pi = 2.0 * acos(0.0);
int n;
double y[100], x[100], r[100];
pair<double, double> ranges[100];
void convertToRange() {
for (int i = 0; i < n; ++i) {
// -pi ~ pi의 범위를 0 ~ 2pi로 변환한다
double loc = fmod(2 * pi + atan2(y[i], x[i]), 2 * pi);
// atan2의 결과가 음수일 수 있으니 0보다 작으면 2pi를 더해준다
double range = 2.0 * asin(r[i] / 2.0 / 8.0);
// 시작 위치와 끝 위치를 저장한다
ranges[i] = make_pair(loc - range, loc + range);
}
sort(ranges, ranges + n);
}여기서 주의할 점은 atan2의 반환 결과가 [-π, π] 범위 안에 있으므로 fmod()를 이용해 강제로 [0, 2π]로 바꾸지만,
ranges에 들어가는 값은 [0, 2π]로 정규화하지 않는 것이다.
뒤에서 알려준다는데 깔끔하게 정리할 자신이 없어서 대충 짚고 넘어가면, 직선 형태로 문제를 변형할 예정인데 0을 포함하는 직선의 경우가 문제가 된다는 걸 생각해보면 간단하게 이해할 수 있다.
📌 선분을 덮는 문제
알고리즘 정당성 증명은 여러 경우의 수를 복잡하게 따져야 하므로 개요만 설명..해준다고 한다.
읽어나 보자.
- 0을 덮는 구간 하나를 선택하면, 해당 구간이 덮지 못하는 구간들로 덮는 문제로 변형할 수 있다.
- 최적해가 0을 덮는 구간을 두 개 넘게 포함할 수 없음을 보이면 된다. (귀류법)
- 0을 덮는 구간이 최적해에 두 개 넘게 포함한 최적해가 있다고 가정해보자.
- 0을 포함해서 왼쪽으로 가장 멀리 가는 A와 오른쪽으로 가장 멀리가는 C가 있다면, 이 두 구간은 모든 구간의 합집합을 덮을 수 있다.
- 만약 0을 포함하는 다른 구간 B가 있더라도 삭제해도 되므로, 우리의 답이 최적해라는 가정이 모순이 된다.
- 따라서, 최적해가 0을 덮는 구간을 두 개 넘게 포함할 수 없다.
- 0을 덮는 구간이 하나라면, 최적해를 찾아낼 수 있음이 자명하다.
- 0을 덮는 구간이 두 개 포함되어 있는 경우엔 어떤 값을 골라야 할까?
- 두 초소의 위치가 0을 사이에 두고 있다면, 어느 구간을 선택하더라도 나머지 부분을 선분으로 펴서 풀면 최적해를 얻을 수 있다.
- 두 초소의 위치가 0을 사이에 두고 있지 않다면, 0에 더 가까운 초소를 선택하는 것이 최적해를 얻을 수 있다는 것을 증명할 수 있다.
- (...왜지? 솔직히 이해가 안 간다. 더 멀리 있더라도 감시 반경이 압도적으로 크면 유리하지 않나? => 막상 코드를 보니까 그냥 0을 포함하는 애들 기준으로 전부 계산 때려보는 거 같은데, 더 이해 안 감)
// 코드 10.6 미나스 아노르 문제를 선형 문제로 변환해서 푸는 알고리즘
const int INF = 987654321;
int n;
pair<double, double> ranges[100]; // 각 원이 덮는 중심각의 구간
// 0을 덮을 구간을 선택하고 나머지를 선형으로 푼다.
int solveCircular() {
int ret = INF;
// 각 구간을 시작 위치의 오름차순으로 정렬한다
sort(ranges, ranges + n);
// 카운터를 이용해 반복적으로 최적해를 계산한다
for (int i = 0; i < n; ++i)
if (ranges[i].first <= 0 || ranges[i].second >= 2*pi) {
// 이 구간이 덮는 부분을 빼고 남는 중심각의 범위는 다음과 같다.
double begin = fmod(ranges[i].second, 2*pi);
double end = fmod(ranges[i].first + 2*pi, 2*pi);
// [begin, end] 선분을 주어진 구간을 사용해서 덮는다.
ret = min(ret, 1 + solveLinear(begin, end));
}
return ret;
}- 각 구간의 시작 위치를 오름차순으로 정렬해두면 solveLinear()를 더 효율적으로 구현할 수 있다.
- 이전에 converToRanges()에서 ranges를 정규화 하지 않았던 것을 이제는 하고 있다는 것에 유의
- 이전에 정규화 안 한 것은 0을 덮는 구간을 식별하기 위함
- 여기서도 안 하면 덮어야 할 중심각 범위에서 시작 위치가 끝 위치보다 커지는 등의 문제가 발생한다.
- 0을 덮는 구간을 하나 선택하고 solveLinear()로 남은 구간을 선택한 결과를 갱신한다.
📌 선형 문제 풀기
// 코드 10.7 선분을 덮는 최소 구간 수를 계산하는 탐욕적 알고리즘
const int INF = 987654321;
// [begin, end] 구간을 덮기 위해 선택할 최소한의 구간 수를 반환한다.
// ranges는 시작 위치의 오름차순으로 정렬되어 있다고 가정한다.
int solveLinear(double begin, double end, const vector<pair<double, double> >& ranges) {
int used = 0, idx = 0;
// 덮지 못한 선분이 남아 있는 동안 계속한다.
while (begin < end) {
// begin보다 이전에 시작하는 구간 중 가장 늦게 끝나는 구간을 찾는다.
double maxCover = -1;
while (idx < ranges.size() && ranges[idx].first <= begin) {
maxCover = max(maxCover, ranges[idx].second);
++idx;
}
// 덮을 구간을 찾지 못한 경우
if (maxCover <= begin) return INF;
// 선분의 덮인 부분을 잘라낸다.
begin = maxCover;
++used;
}
return used;
}- 회의실 문제와 비슷하지만, 겹치는 구간이 존재한다는 것에서 다소 다르다.
- 여기서 가장 이득인 선택은 "오른쪽으로 가장 멀리 가는 구간"을 택하면 된다.
- 선분의 맨 왼쪽 점을 포함하는 구간 중, 가장 오른쪽으로 가는 구간 a 대신 b를 선택한 최적해가 있음을 가정하자
- 최적해에서 b를 빼고 a를 넣으면 크기가 같은 또 다른 답을 얻음을 알 수 있다.
- 따라서 a를 포함하는 최적해는 반드시 존재하므로 탐욕적 선택 속성이 성립한다.
- begin 전에 시작하는 구간 중 가장 오른쪽에서 끝나는 구간을 찾아 선분을 덮고, 덮인 부분을 잘라내는 과정을 반복하면 된다.
- 이미 solveCircular()에서 시작 위치가 빠른 순서로 정렬했으므로 선형 시간으로 해결할 수 있다.
⏲️ 시간 복잡도
- solveCircular() 함수는 solveLinear()를 최대 n번 호출한다.
- solveLinear()는 2중 반복이지만, 내부의 while은 n개 구간에 대해 최대 한 번씩만 실행되므로 O(n)이 된다. (4.5절에서 다룰 분할 상환 분석의 한 예시)
- 따라서 전체 시간복잡도는 \(O(n^{2})\)이 된다.