[Database] 물리적 설계

📕 목차

1. 데이터베이스 물리적 설계
2. 파일 구성
3. 접근 방법 설계

1. 데이터베이스 물리적 설계

📌 Concept

def. Logical Schema → 효율적인 Physical Database 구성
물리적 데이터베이스 구조
- 저장 레코드 형식, 저장 순서, 접근 경로, 물리적 저장 장치의 할당 등에 대한 내역
참고 사항
- 물리적 DB 구조는 세부적인 성능에 영향을 미친다.
- 물리적 설계 단계에서 고려할 사항들의 대부분은 특정 DBMS에 의해서 해결된다.
- DBA만이 물리적 DB 구조의 구성에 관여할 수 있음

2. 파일 구성

• Concept
• 고정길이 레코드(Fixed-Length Records)
• 가변 길이(Variable-Length) 레코드
• 파일에서 레코드 저장 방법
• 순차 파일 구성(Sequential File Organization)
• 다중-테이블 클러스터링 파일 구성

📌 Concept

파일 구성
- 데이터베이스는 여러 개의 File로 저장
- File은 여러 개의 Record를 저장
- Record는 여러 개의 Field로 구성
- (File → Record → Field)
가장 단순한 데이터베이스 구성 방법 ⇒ 문제가 많지만 구현 쉬움
- 레코드 크기 고정
- 한 파일에는 한 종류의 레코드만 저장
- 하나의 릴레이션은 하나의 파일로 매핑
고려 사항
- 레코드 표현 방법 (고정 vs. 가변)
- 파일에서 레코드 저장 방법 (순차 vs. 클러스터링)

📌 고정길이 레코드(Fixed-Length Records)

모든 record 길이 동일
n이 레코드 길이라면, i번째 레코드는 n*(i-1)에 저장
블록의 경계를 넘어서는 레코드는 없도록 강제 (구현 용이)
i번째 레코드가 삭제된 경우 3가지 구현 방법
- 아래 레코드들을 한 칸 씩 위로 이동
- 마지막 레코드를 i번째로 이동
- Free List로 연결

🟡 Free List

파일 header에 삭제된 record들을 연결 리스트로 묶는다.
각각의 삭제 레코드에 다음 삭제 레코드의 위치를 저장

📌 가변 길이(Variable-Length) 레코드

발생 원인
- 한 파일에 다양한 타입의 레코드를 저장할 경우
- 레코드가 varchar 타입의 필드를 가지고 있을 경우
- 레코드에 배열 타입의 필드를 가지고 있을 경우

가변 길이 필드 표시를 위한 한 가지 방법
- 필드 순서 고정
- 가변 필드 위치에 (offset, length)의 고정된 정보만 저장
- 실제 데이터는 offset 위치에 저장
- Null-value bitmap: 속성당 1bit, Null 속성은 1로 set

🟡 가변 길이 레코드를 위한 블록 구조

Block Header
- record 수, 각 record의 위치와 크기
- 빈 공간의 마지막 위치 (구현에 따라 다르게 표시)
recod id = (block #, slot #)
- block 내에서 record 위치는 이동 가능 ← slot 내용 변경
- slot #는 고정

📌 파일에서 레코드 저장 방법

Heap 방식
- File 내에 임의의 위치
순차 파일 구성
- record를 key 순서대로 저장

Hashing
- key에 대한 hash를 record의 저장 위치로 결정
- 고정 길이에서만 가능
- 매우 빠르지만 가변 길이는 불가능하다. (순차/구간 탐색 불가)
다중-테이블 클러스터링 파일 구성
- 여러 개의 릴레이션을 하나의 파일에 저장
- 관련된 record들을 하나의 block에 같이 저장

📌 순차 파일 구성(Sequential File Organization)

전체 파일을 순서대로 처리할 경우 적합
record들을 검색 키의 순서대로 정렬
동작 방식
- 삭제: 포인터 체인을 변경
- 삽입: 레코드가 저장될 위치를 파악한 후 공간이 있으면 삽입, 없으면 overflow 블록에 추가
- 주기적으로 재구성

📌 다중-테이블 클러스터링 파일 구성

여러 개의 릴레이션을 한 파일에 저장
장점: 관련있는 릴레이션의 Join 연산 속도↑
단점
- `select * from department;` 구분하기 위한 overhead 발생
- 가변 길이 레코드를 처리할 수 있어야 한다.

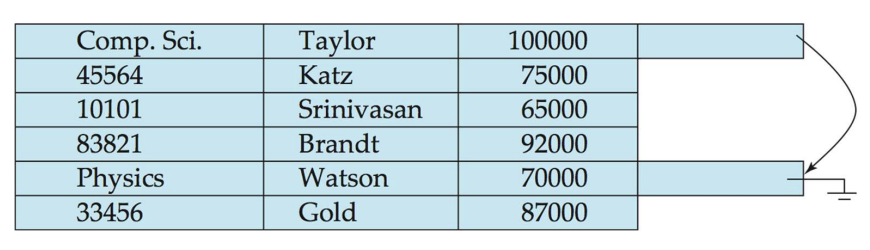
Department 테이블에 대한 효과적인 질의 처리를 위해, 레코드들을 연결 리스트로 묶는 방법도 가능

3. 접근 방법 설계

• Concept
• B tree
• B* tree
• B+ tree
• B-Tree Family 비교
• 보조 인덱스
• 역 인덱스 (역 파일)
• 다중 리스트 파일(Multi-list File)
• 역 인덱스 vs. 다중 리스트

📌 Concept

접근 방법(Access Method) == 색인 구조
- "Query 받으면 어떤 자료구조를 사용해서 결과에 다다르게 할 것인가?"
- 저장 구조와 검색 기법으로 구성
인덱스
- record 검색 시 빠른 access 보장
- 주로 B+ Tree로 구현
- 자주 검색되는 field에 index를 생성하면 검색 연산이 빨라진다.
- 값의 구간에 의한 접근과 우선 순위에 따른 접근이 가능하다.
- 종류
  - 유일 인덱스: 키 값의 중복을 허용하지 않음
  - 보조 인덱스: 키 값의 중복을 허용 (중복은 있으나, 자주 사용되는 레코드들)
Hashing
- 특정한 하나의 값의 연산 결과로 저장 위치를 파악
- 값의 구간에 의한 접근은 불가능
- 오로지 그 값에 대한 검색만 가능
Clustering
- 연관된 레코드를 물리적으로 인접한 공간에 저장

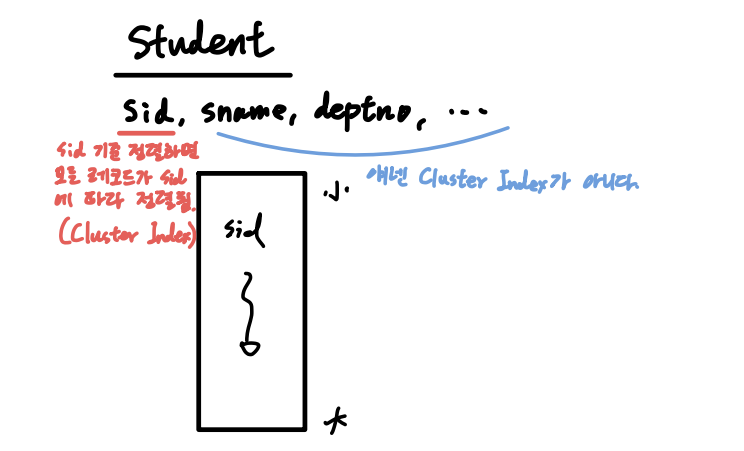
Clustered Index
- 데이터 레코드의 저장 순서와 인덱스 내의 순서가 동일
- 하나의 테이블에는 하나의 Clustered Index만 존재

📌 B tree

B Tree
- Memory Index 구조가 아닌, File Index 구조
- "B" : Balanced, Boeing, Bayer, ...
- 하나의 노드에 {key, data path, child pointer} 저장
속성
- 각 노드(=block)는 최대 m개의 포인터를 가질 수 있다.
- Root와 Leaf를 제외한 모든 노드들은 적어도 m/2개의 child를 가져야 한다.
- Leaf가 아닌 Root는 적어도 2개의 child를 가져야 한다.
- 모든 Leaf 노드들은 동일한 level에 위치한다.
- Leaf가 아닌 노드가 k개의 child를 가질 경우, 그 노드는 k-1개의 key를 가져야 한다.
- 각 노드에서 key들은 순서대로 정렬되어야 한다.

🟡 m이 4인 B tree 예시 (4차 B tree)

🟡 B tree 삽입, 삭제

[자료구조] B-트리(B-Tree)란? B트리 그림으로 쉽게 이해하기, B트리 탐색, 삽입, 삭제 과정

B- 트리란? 보통 B 트리라고 하면 B- 트리를 의미한다. B 트리는 트리 자료구조의 일종으로 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다. 이러

code-lab1.tistory.com

삽입 과정
1. tree가 비어있다면, root 노드를 할당하고 데이터를 삽입하고 종료한다.
2. tree가 비어있지 않다면, 삽입할 데이터를 오름차순으로 넣기 위한 leaf 노드를 찾는다.
3. leaf node에 빈 공간이 있다면 데이터를 할당하고 종료한다.
4. leaf node가 더 이상 key를 가질 수 없어 overflow가 발생한 경우 재분배를 시작한다.
  - 노드의 중앙값에 해당하는 key를 기준으로 좌우 key들을 분리한다.
  - 선택된 key는 parent 노드로 승진한다.
  - 만약 parent 노드에서도 overflow가 발생한다면, 4번 과정을 재귀적으로 수행한다.
삭제 과정 (복잡하니까 대충 요약)
1. 선택한 노드 삭제 후, parent pointer가 m/2보다 크다면, 그대로 종료한다.
2. key가 부족해지는 경우 부모나 형제에게서 빌려오는 등 재배치 과정이 필요하다.

📝 예제

B tree 규격이 다음과 같다고 가정하자.

node size = 1,000 byte
key size = 80 byte
child pointer = 10 byte
data path = 10 byte

1️⃣ 각 노드가 가질 수 있는 자식 노드 수(m)의 최대값

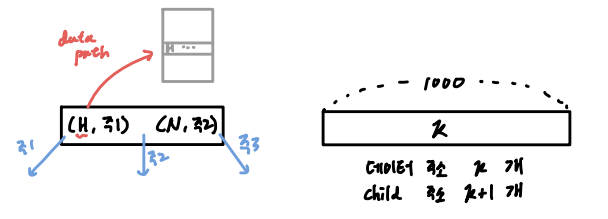
자식 노드 수(m)을 가질 때,
- key 개수 = m-1
- data path 개수 = m-1
- child pointer 개수 = m
node size = 80 byte * (m-1) + 10 byte * (m-1) + 10 byte * (m)
= 100m - 10 byte (≤ 1,000 byte)

∴ m 최댓값 = 10

2️⃣ 루트와 리프 노드를 제외한 노드가 가질 수 있는 자식 노드 수의 최소값

root와 leaf 노드를 제외한 모든 노드는 적어도 m/2개의 자식 노드를 가져야 한다.

∴ 답: 5

3️⃣ 90개의 key를 저장할 경우 트리의 최대 깊이

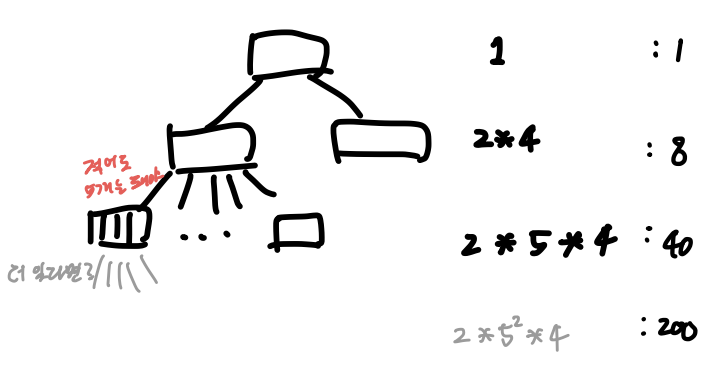
모든 노드가 최소한의 자식만을 가지면 된다.
root는 적어도 2개의 자식만 가지면 된다.
internal 노드는 적어도 5개의 자식을 가져야 한다.
깊이가 3에 도달하면, 표현 가능한 key의 수가 249개 이므로 더 이상 내려갈 수 없다.

∴ 답: 3

4️⃣ 90개의 key를 저장할 경우 트리의 최소 높이

모든 노드가 최대한의 자식을 가져야 한다.
root에 key를 8개 채운다면 가능한가?
- 8 + 9 * 9 = 89 이므로 모든 key를 채울 수 없다.
root에 key를 9개 채운다면 가능한가?
- 9 + 9 * 10 = 99 이므로 모든 key를 표현할 수는 있다.
- 하지만 자식 노드의 최소 child pointer 개수를 충족하지 못 하므로 불가능하다.
따라서 최소 깊이 2까지는 내려가야 한다.

∴ 답: 2

📌 B* tree

한 쪽의 sibling이 full 될 때까지 재분배
root를 제외한 모든 노드들은 적어도 (2m - 1)/3개의 pointer(child 혹은 data)를 가져야 한다.
ont-to-two split ↔ two-to-three split
- 분리되는 시점을 2/3까지 늦출 수 있다.
- 깊이↓ 읽어야 하는 # blocks↓ 속도↑
root 노드에서 split 해결 방법
- root node size = 4/3 * 일반 node size
- root node split은 one-to-two split으로 간주

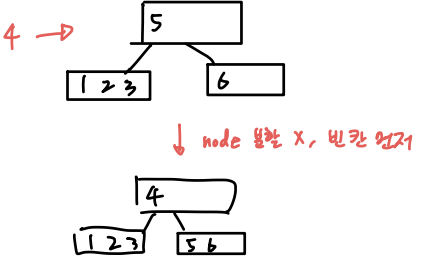
🟡 A Two-to-Three Split

📌 B+ tree

인덱스 세트(Index Set)
- leaf 노드가 아닌 노드들
- leaf 노드까지의 access 경로 제공
- data 주소 정보를 포함하지 않는다. (index set node가 가지는 정보 = {key, child pointer})
- 특정 key 값을 갖는 record를 access할 때 사용
순차 세트(Sequence Set)
- leaf 노드
- data 주소 정보 포함 (data를 조회하려면 반드시 leaf 노드까지 탐색해야 한다)
- 인접 leaf 노드 간에 연결리스트 구성 ⇒ 순차(구간) 검색 가능
속성
- B tree와 node 조건에 대한 속성을 공유한다.
- Non-leaf node 구조: <n, P0, K1, P1, K2, K2, …, Kn, Pn> (단, K = key, P = page 주소)
- Leaf node 구조: <q, <K1, R1>, …, <Kq, Rq>, Pnext> (단, R = record, Pnext = 다음 Leaf 주소)

🤔 B tree와 B+ tree의 깊이에 대하여

B tree는 모든 노드가 {Key, Data path, Child pointer}를 관리하는 반면,

B+ tree는 구분자로 Leaf node까지 탐색하여 결과를 찾아내야 하므로, "언제나 B+ tree의 깊이가 B tree보다 깊어질까?"

물론 거짓이다.

오히려 더 적을 수도 있다.

예를 들어, 이전 예제의 tree spec을 그대로 들고와보자.

B tree node는 하나의 node가 가질 수 있는 최대 자식 수는 9개다.

하지만, B+ tree는 80*m + 10*(m+1) ≤ 1,000이므로 최대 10개의 자식을 가질 수 있다.

따라서, 경우에 따라선 B tree보다 깊이가 얕아질 수도 있다.

🟡 B+ tree의 Index Set 변경 과정

Sequence set의 block이 분할될 때, 새로운 separator가 index set에 추가되어야 한다.
Sequence set의 block들이 연쇄될 때, 기존 separator가 index set에서 삭제되어야 한다.
Sequence set의 block들 사이에 record가 재분배될 때, index set의 separator도 같이 변화되어야 한다.
- 재분배(redistribution): key를 바로 옆 노드로 보낼 수 없으므로, 옮길 노드를 parent 노드로 올리고 parent 노드를 sibling 노드로 보내는 것

[자료구조] 그림으로 알아보는 B+Tree

정렬된 순서를 보장하고, 멀티레벨 인덱싱을 통한 빠른 검색과 선형탐색까지 가능한 실전형 자료구조 B+ 트리입니다.

velog.io

삽입 동작
1. leaf node가 full 상태가 아니라면 오름차순 정렬에 맞게 삽입하고 종료
2. leaf node가 full 상태라면, 새로운 leaf 노드를 구성하고 기존 leaf 노드 데이터 절반을 옮긴다.
3. 새로운 leaf 노드의 최소 키(나누기 전 중앙값)를 parent 노드에 삽입
4. parent 노드에서 overflow 발생 시, 2번 과정 재귀적 수행
5. root가 쪼개지면 새로운 root 노드를 생성
  - 1개 key와 2개의 child pointer로 구성되어야 한다.
  - 기존 root 노드의 중간 key는 새로운 root 노드에 저장한 뒤 제거한다.
삭제 동작 (삭제할 key k는 반드시 leaf node에 존재한다.)
1. 삭제할 key k가 index에 없고, leaf node의 가장 처음 key가 아니라면 k를 제거하고 종료
2. 삭제할 key k가 leaf node의 가장 처음 key인 경우 (반드시 index에 존재), 형제 노드의 key를 빌리거나 부모 key와 병합하는 과정 동일
3. leaf node 간에 병합할 때는 parent key == 오른쪽 child noe 처음 key이므로, 부모 key를 가져오는 과정만 생략

📝 예제

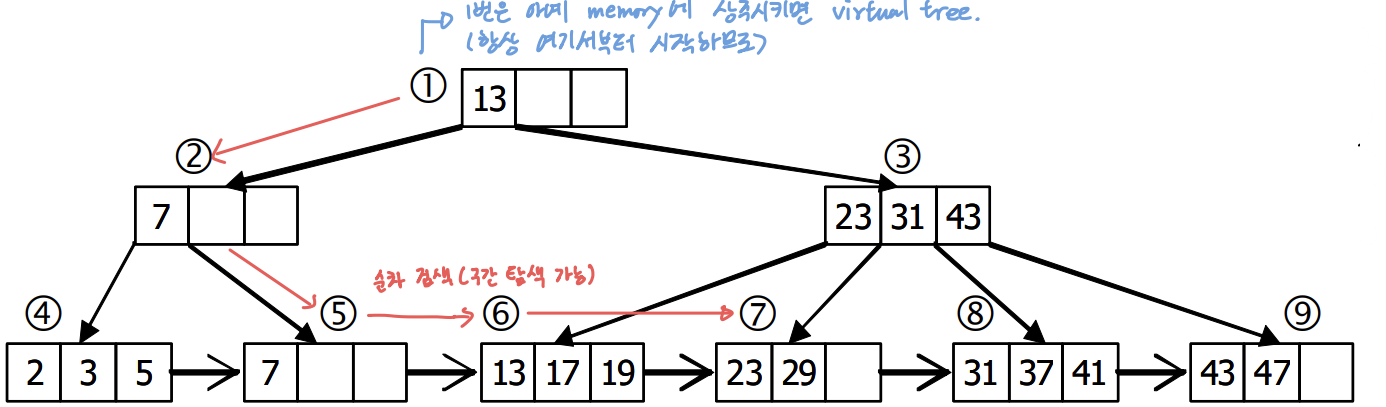
1️⃣ 10 ≤ key ≤ 20 사이의 record 검색할 시, access되는 노드 순서

답: 1 → 2→ 5 → 6 → 7

2️⃣ 14를 추가한 후의 B+ tree

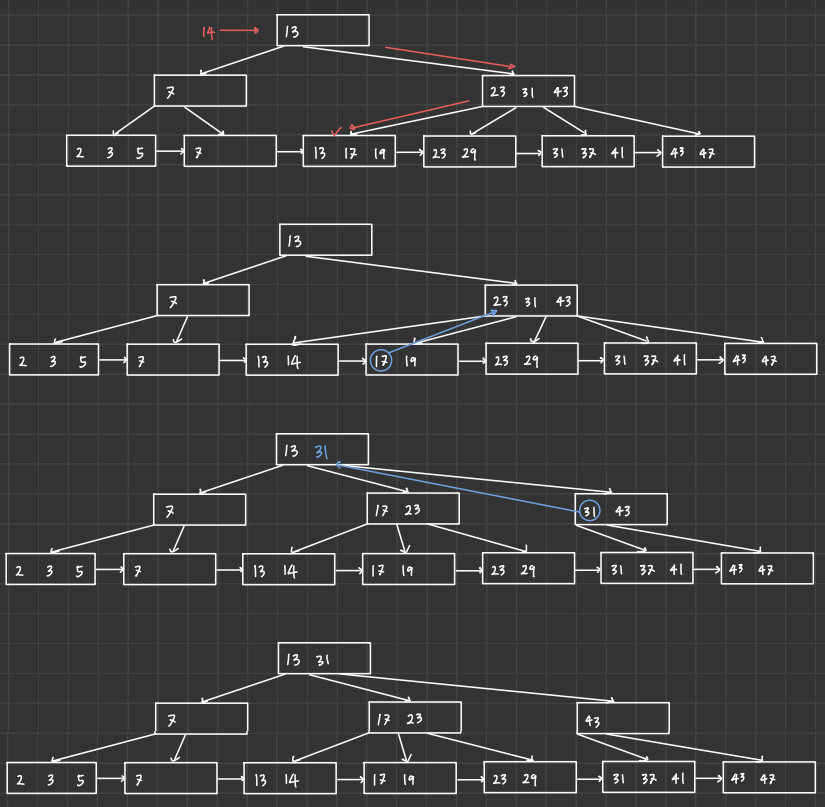
14가 들어갈 leaf node를 탐색한다. (overflow → 분할 시작)
{13, 14, 17, 19}를 절반으로 나눠서 {13, 14}, {17, 19} leaf node로 재구성
{13, 14, 17, 19}노드에서 중앙값({17, 19} 노드 최소값)을 부모 노드의 key로 승격 (overflow)
{17, 23, 31, 43}을 절반으로 나누어 {17, 23}, {31, 43}으로 재구성 → 중앙값인 31 승격
기존 internal node의 중간 key인 31 제거

3️⃣ 7을 삭제한 후의 B+ tree

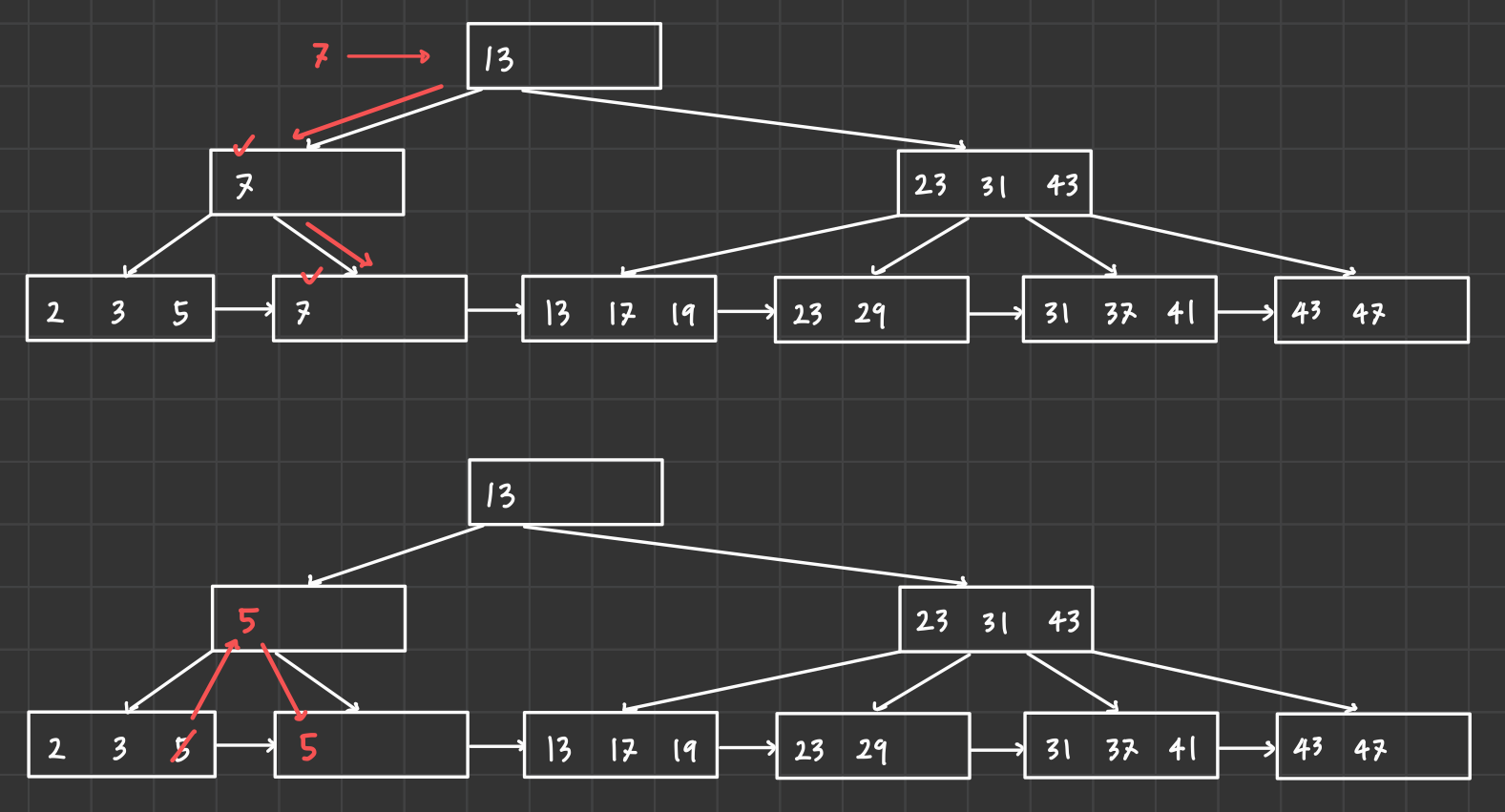
7을 삭제할 시 최소 키 조건 충족 불가능
오른쪽 sibling node의 가장 큰 key 값을 빌려온다.
해당 key를 승격시킨다.

📌 B-Tree Family 비교

공통점
- Paged index structure
- height-balanced trees
- 상향식 tree 성장
- Greater storage efficiency (1-to-2, 2-to-3)
- Virtual tree structures 지원 가능
- Variable-length record 지원 가능

B-Tree Family가 항상 최선의 선택은 아니다.

구현이 복잡하다.
Index 크기가 작다면, simple index로 충분하다.
Random Access가 주로 발생한다면 hashing을 고려하라

🟡 B Tree

모든 노드에 {key, data path, child pointer}를 나누어 저장
데이터를 탐색하기 위해 반드시 Leaf node까지 갈 필요 없다.
B+ tree보다 적은 공간을 차지하지만, data record에 대한 pointer가 필요하다.
- tree 깊이 자체는 더 커질 수도 있다.
In-order traversal을 이용한 sequential search가 가능하다.
- Disk는 Random access가 아니므로 더 오래 걸린다.

🟡 B+ Tree

Leaf node들이 linked list 구조로 연결
- 순차 탐색 가능
- 구간에 대한 query 처리 가능
Tree Order 증가
- Internal node가 data에 대한 pointer가 불필요 하므로, 더 많은 자식 노드를 가질 수도 있다.
Deletion 과정이 상대적으로 단순하다. (모든 key가 반드시 leaf node에 존재하므로)
Leaf 노드와 Non-leaf 노드 구조가 거의 동일하다.

Prefix B+ tree 구성 가능
- Internal node의 fan-out 감소
- Tree의 깊이 감소 & 공간 효율성 증가

🟡 B Tree와 Hashing 비교

단일 데이터 조회(Point Query)에 대해선 Hashing이 빠르다.
구간 데이터 조회(Range Query)에 대해선 Indexing이 빠르다.

📌 보조 인덱스

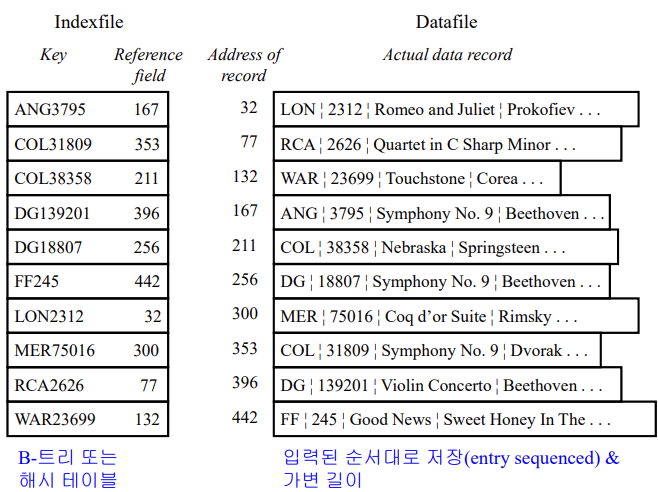
중복을 허용하는 인덱스
베토벤의 9번 교향곡에 대한 모든 데이터를 불러와야 한다면, 어떻게 빠르게 조회할 수 있을까?
- 양이 너무 많아서 순차 탐색으로도 오래 걸린다.
(key, value) 쌍에서 value에 어떤 값을 저장할 것인가?
- data record 주소: 간단하고 빠른 접근
- primary key: 안전성 우수
중복 키 저장 방법
- 역 인덱스 (Inverted Index)
- 다중 리스트 (Multi-list File) ⇒ 단점이 너무 명확

1️⃣ Index File 문제1. 작곡가에 대한 색인(1): value에 data record 주소 저장

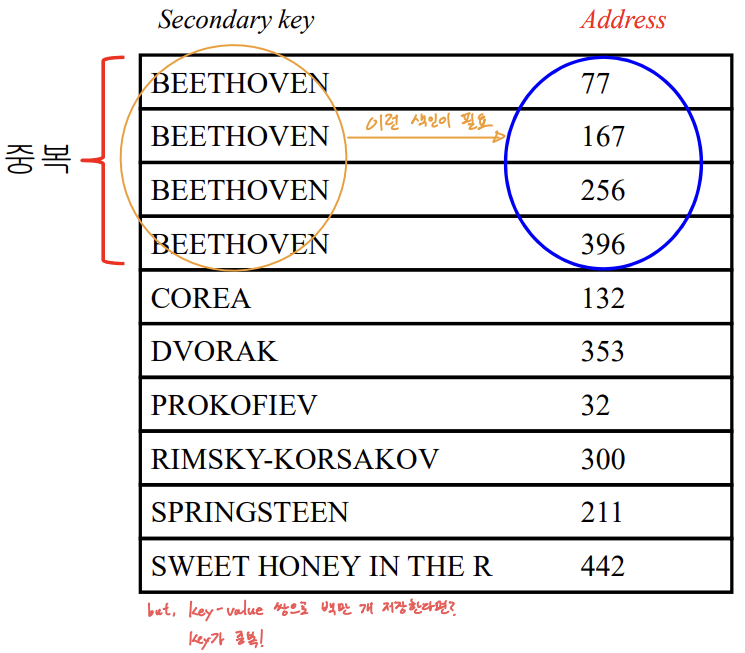
2️⃣ Index File 문제2. 작곡가에 대한 색인(2): value에 primary key 저

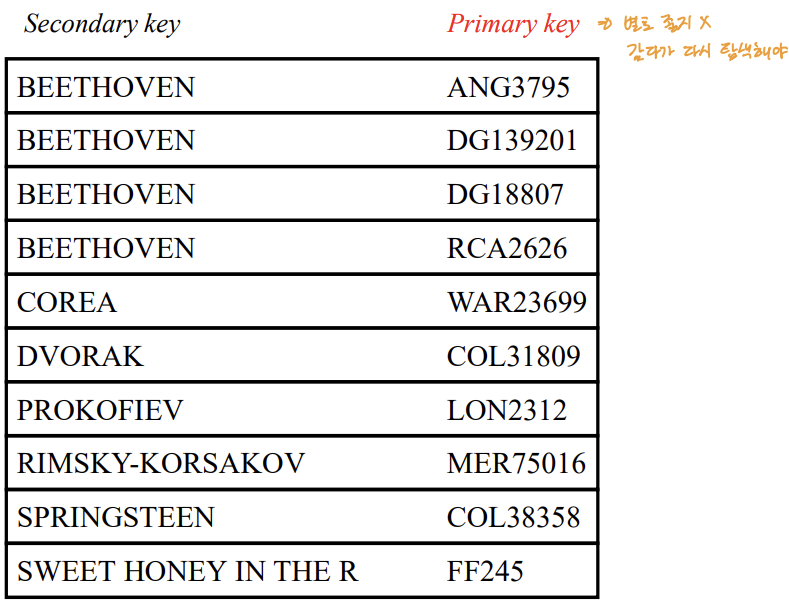
3️⃣ Index File 문제3. 제목 인덱스

📌 역 인덱스 (역 파일)

보조 인덱스를 array 구조로 구현
새로운 record 첨가 시, array에 포함
주어진 key에 대한 array space 한계
Internal Fragmentation

🟡 작곡가 인덱스 개선

구조체로 만든다면 address를 가변 길이로 만들어야 한다.
데이터가 너무 방대해진다면 압축도 필요하다.

📌 다중 리스트 파일(Multi-list File)

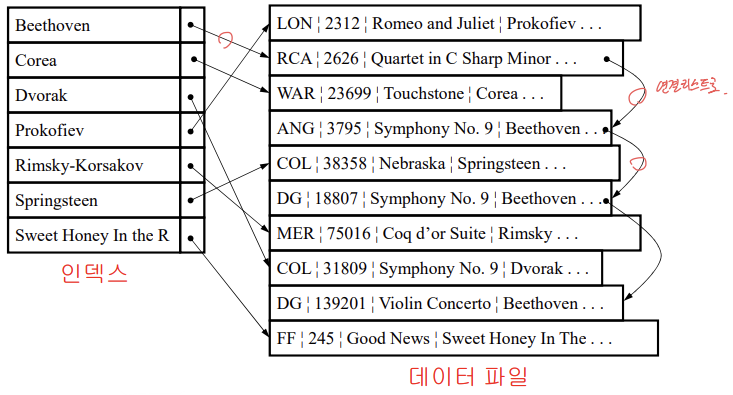
보조 키에 대한 다중 리스트 인덱스 파일 + 데이터 파일(각 보조 키에 대한 link field)
단점이 명확하다
- 탐색이 너무 오래 걸린다.
- index file에 보조 인덱스를 몇 개 만들지 고정이 안 되어 있다. (다른 보조 인덱스 추가하면, link를 더 추가?)

📌 역 인덱스 vs. 다중 리스트

	역 인덱스	다중 리스트
인덱스 구성	가변 길이	고정 길이 (인덱스 관리 용이)
데이터 파일 변경 여부	변경 불필요 (index를 사용하지 않는 프로그래머에게 투명하다.)	변경 필요 (보조 인덱스 수만큼 링크 필드 추가)
검색 처리	경우에 따라 data file access 필요없이, index file에서 처리 가능	대부분 data file 접근 필요

저작자표시 비영리

1. 데이터베이스 물리적 설계

2. 파일 구성

3. 접근 방법 설계

티스토리툴바