[Database] 데이터 종속성과 정규화

📕 목차

1. 관계형 데이터베이스 설계의 문제점
2. 분할
3. 함수 종속성
4. 함수 종속성을 이용한 정규화
5. 다중치 종속성을 이용한 정규화

1. 관계형 데이터베이스 설계의 문제점

📌 잘못된 데이터베이스 설계

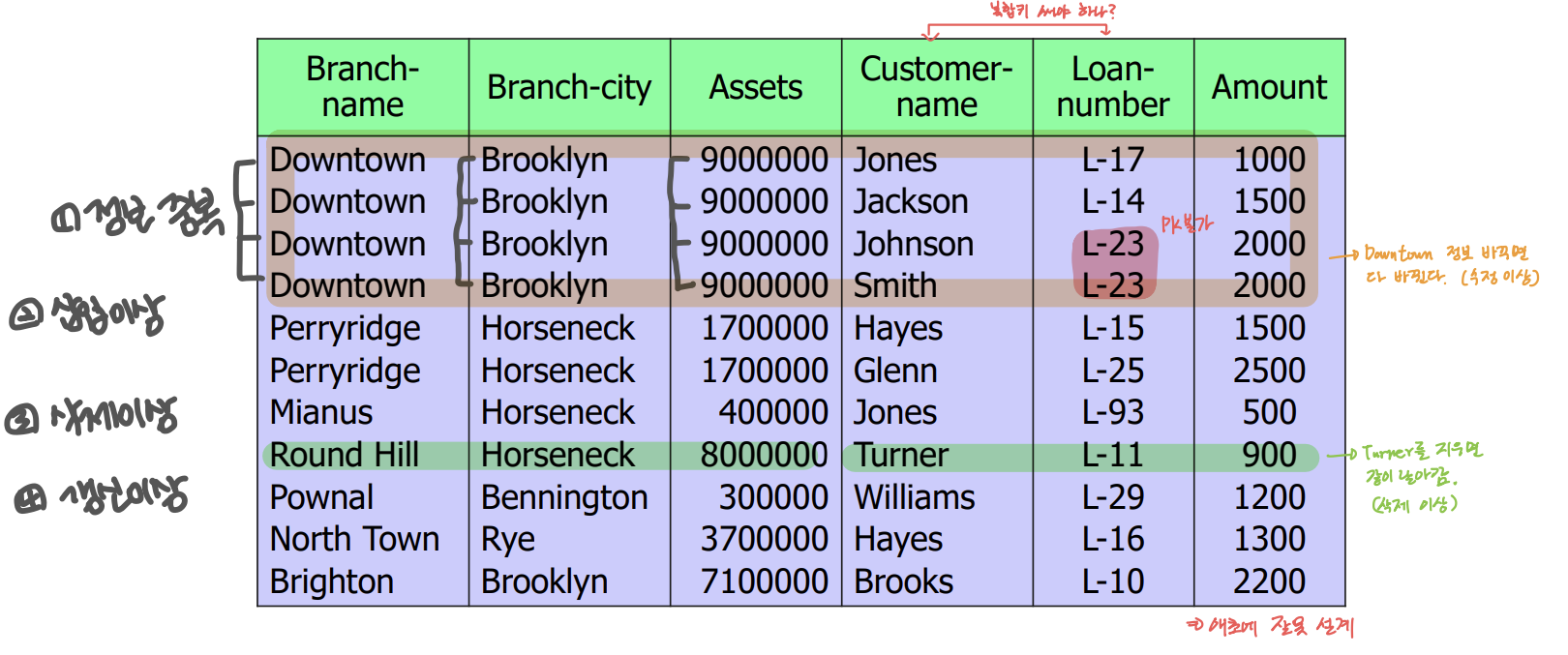
정보의 중복
- Branch 정보의 중복
특정 정보를 나타낼 수 없음
- 삽입 이상(Insert Anomaly) : 계좌가 없는 Branch 정보를 입력?
- 삭제 이상(Delete Anomaly) : L-29 계좌 삭제 → Pownal 지점 정보 삭제
- 갱신 이상(Update Anomaly) : Downtown 지점의 Asset이 변경됨

2. 분할

📌 정보 중복 및 이상 현상을 해결하는 방법

릴레이션을 분할한다.
단, 잘못된 분할은 정보 손실(Information Loss)을 초래한다.

❌ 잘못된 분할

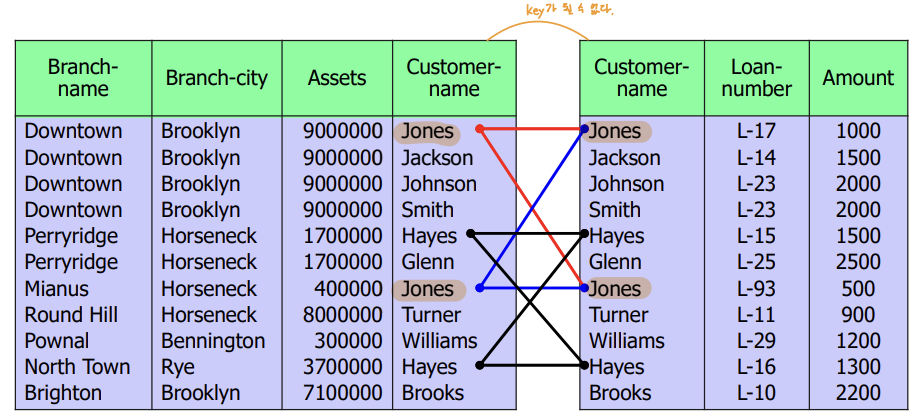
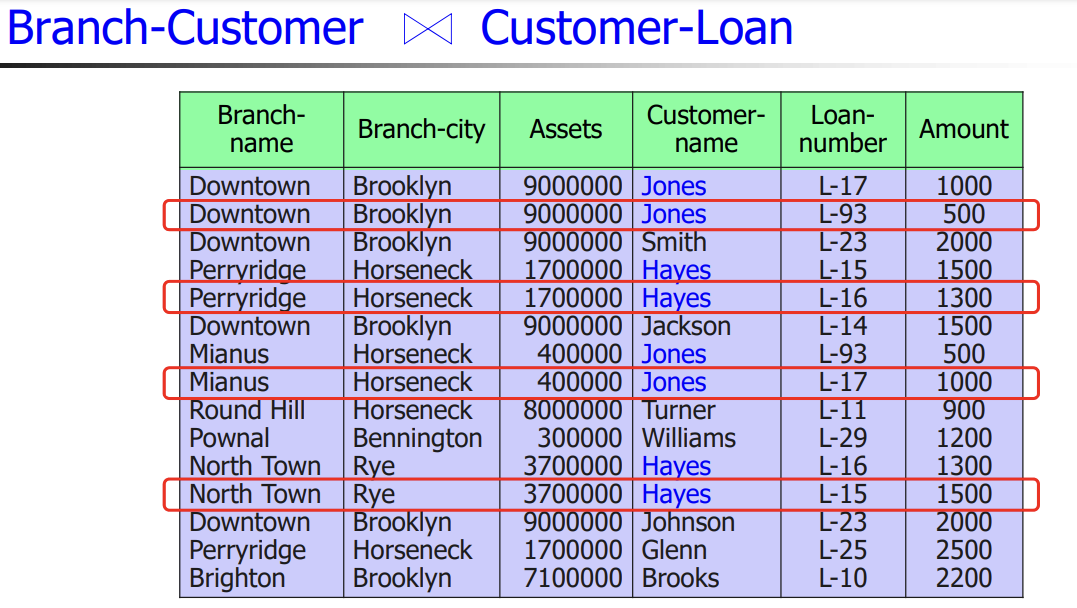
위 테이블을 조인하면 레코드가 2개여야 하는 Jones와 Hayes가 4개가 된다.

📌 무손실 조인 분할(Lossless Join Decomposition)

분할(Decomposition)
- R: 테이블 r의 스키마
- {R1, R2, ..., Rn}: Decomposition of R, if) R = R1 ⋃ R2 ⋃ ... ⋃ Rn (분할된 테이블을 모두 조인했을 때, 모든 속성 조합이 표현 가능한가?)
- 단, 위 조건을 충족한다고 무손실 Join 분할이 되진 않는다.
무손실 조인 분할
- "Join 했을 때, 모든 값이 원상복구 되는가?"
- {R1, R2, ..., Rn}: Lossless Join Decomposition of R, if) r(R) = r(R1) ⨝ r(R2) ⨝ ... ⨝ r(Rn)
- 위의 조건을 만족하지 않을 경우, 손실 조인 분할(Lossy Join Decomposition)에 해당한다.

3. 함수 종속성

📌 기본 개념

함수 종속성(Functional Dependency): α→β
- α, β : 테이블 r의 속성
- r의 임의의 두 레코드 t1, t2에 대해, t1[α] = t2[α]이면 반드시 t1[β] = t2[β]일 경우에 α→β 성립 (이게 진짜 중요)
- 각각의 속성의 부분 집합 X,Y에서 X의 값을 알면 Y의 값을 바로 식별 가능하며, X의 값에 따라 Y의 값이 달라질 때, Y는 X에 함수적 종속이라고 표현한다. (X: 결정자, Y: 종속자)
예시. Loan = (branch-name, loan-number, customer-name, amount)
- loan-number → amount
- loan-number → branch-name
- loan-number → customer-name : loan-number가 같다고 customer-name도 같을 것이라고 보장할 수 없다. 하나라도 틀리면 종속성 성립 불가

📝 예시. 종속성 찾기

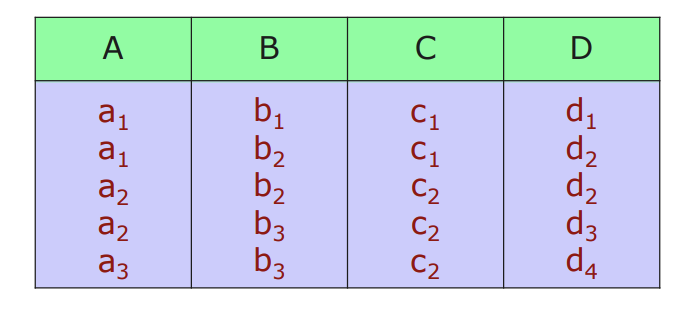
A → C
AB → D
- AB가 같은 케이스가 없는데, 어떻게 두 번째가 성립하는가?
- 논리식 p => q, β가 같든말든 AB는 항상 다르면 참이 성립한다.

🟡 tip

key → ? : 언제나 참
α → β : (true, false)일 때만 거짓. (논리식에 의해)

📌 함수 종속성 집합의 Closure

함수 종속성 집합 F의 Closure: F⁺ (너무 많아서 딱히 의미는 없는데, 찾을 수 있어야 한다.)
- def. F에 의해 논리적으로 유도될 수 있는 모든 함수 종속성들의 집합
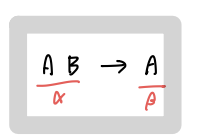
- 단순 종속성(Trivial Dependency)
  - 속성 α가 속성 β를 포함하면, α→β는 단순 종속성
  - 정의에 의해 "A(true) → A(true) ?"는 언제나 참이므로, "AB(true) → A(true) ?"도 언제나 참.
- 부분 종속성(Partial Dependency)
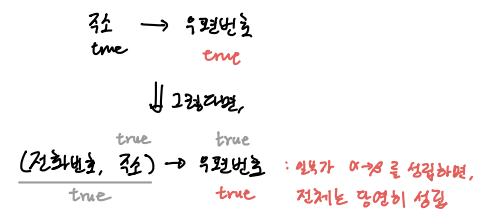
  - α→β가 성립하며, ɤ⊂α인 속성 ɤ에 대해 ɤ→β도 성립한다면, β는 α에 부분적으로 종속 (일부가 α→β 성립하면, 전체는 당연히 성립한다.)
  - 즉, 종속자가 (1)기본키가 아닌 다른 속성에 종속되거나, (2)기본키를 구성하는 속성 중 일부만 종속되는 경우
  - ex. (지점 주소, 전화 번호) → 우편 번호 : 우편 번호는 지점 주소만 알아도 식별 가능하므로, 우편 번호는 기본키에 부분 함수 종속된 관계다.
Armstrong의 원칙
1. 기본 규칙
  - 반사(Relexivity): α→β for β⊆α (A→B, AB→A 모두 성립)
  - 첨가(Augmentation): If α→β and ɤ⊆R. then ɤα→ɤβ (A→B가 이미 성립한다면, ɤα→ɤβ도 성립)
  - 이행(Transitivity): If α→β and β→ɤ, then α→ɤ (정/역 모두 성립)
2. 추가 규칙
  - 결합(Union): If α→β and α→ɤ, then α→βɤ (역은 성립 X)
  - 분할(Decomposition): If α→βɤ, then α→β and α→ɤ
  - 의사 이행(Pseudotransitivity): If α→β and ɤβ→δ, then αɤ→δ

🟡 예제

💡 key가 되려면, 함수의 Closure가 모든 레코드에서 다르면서 다른 속성을 모두 포함해야 한다.

예제 스키마와 함수 종속성
- R = (A, B, C, G, H, I)
- F = {A→B, A→C, CG→H, CG→I, B→H}
  1. A가 같으면 B, C, H가 같다. A → BCH (key가 되려면, 모든 레코드에서 A가 달라야 한다!!)
  2. AG→H(A→H이므로 생략 가능), AG→I
F⁺에 포함되는 종속성
- A → H
- CG → HI
- AG → I => 후보키
Q. R의 key 속성은 무엇인가?
- AG

📌 속성 집합의 Closure

속성 α의 Closure: α⁺
- α에 함수적으로 종속되는 모든 속성들의 집합
- ex. A⁺ = (ABCH)
- ex. (AG)⁺ = ABCGHI : R의 후보키 (모든 속성을 포함)
α⁺를 계산하는 알고리즘

📝 예제

과정
- A→DE 이므로, AB→CDE
- B→F 이므로, AB→CDEF
- F→GH 이므로, AB→CDEFGH
- D→IJ 이므로, AB→CDEFGHIJ
R에 대한 후보키: AB
R을 R1=(A,B,C,D,E), R2=(B,F,G,H), R3=(D,I,J)의 3개의 Relation으로 분리한 경우
- lossless Join 분할 성립
- dependency preserving 성립

📌 Canonical Cover

필요성
- 함수 종속성은 무결성 제한 조건
- DB의 변경이 발생할 때마다 FD의 유지 여부 검사
- Closure가 동일한 여러 개의 FD가 존재한다면, 가급적 단순한 FD를 선택하여 구현
  - {A→B, A→C}, {A→BC}, {A→B, A→C, A→BC}
군더더기 속성(Extraneous Attributes) => 찾아서 없애라
- Attribute A is extraneous in α, if A ∈ α, and F logically implies (F - {α→β}) ⋃ {(α - A)→β}
- Attribute A is extraneous in β, if A ∈ β, and (F - {α→β}) ⋃ {α→(β - A)} logically implies F
- B→C면, AB→C (A가 군더더기)
- {A→B, B→C, A→BC} (C가 군더더기)

📌 정의와 알고리즘

함수 종속성 집합 F에 대한 Canonical Cover Fc를 정의
- Fc ⇒ F and F ⇒ Fc
- Fc의 모든 종속성은 군더더기 속성을 포함하지 않는다.
- If α1→β1 and α2→β2 in Fc, then α1 ≠ α2
  α1→β1과 α1→β2fmf α1→β1β2로 통합하라.
알고리즘

🟡 예제

예제 스키마
- R = (A, B, C)
- F = {A→BC, B→C, A→B, AB→C}
Canonical Cover 계산
1. A→BC and A→B를 A→BC로 합친다.
2. AB→C에서 A는 군더더기 속성이므로 B→C로 치환
3. (1)의 A→BC에서 C는 군더더기 속성이므로 A→B로 치환
Canonical Cover: A→B, B→C

4. 함수 종속성을 이용한 정규화

아, 정규화 어렵네.

내용 이해했다 생각해서 문제 푸는데 잘 안 풀린다.

📌 분할의 바람직한 속성

두 가지 속성
- 무손실 조인 분할
- 종속성 보전 분할
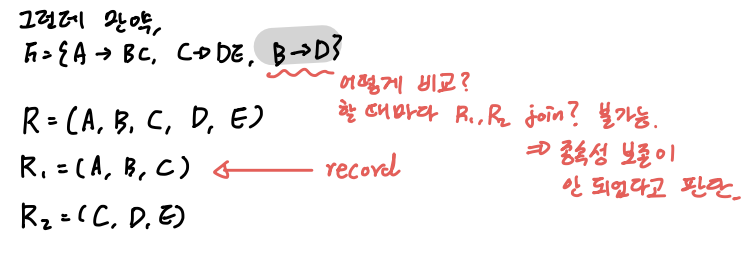
매번 JOIN을 해봐야 무손실 조인 분할을 판단할 수 있는 것은 아니다.
1. R1과 R2를 R의 분할이라고 가정
2. (R1 ∩ R2) → R1 or (R1 ∩ R2) → R2가 성립하면 무손실 조인 분할
  - R=(A,B,C,D,E), R1=(A,B,C), R2=(C*,D,E)
  - 만약 C1이 2개라면, 조인 결과가 4개나 발생한다.
  - 즉, 둘 중 하나는 pk여야 한다. (fk는 중복일 수도 있다.)

🟡 종속성 보전(Dependency Preserving)

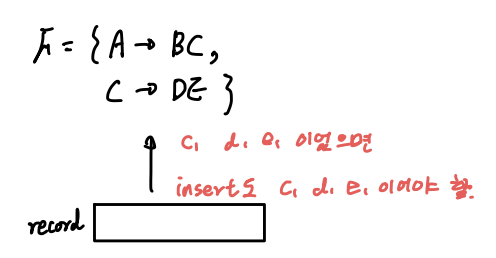
def. 각각의 Table로 종속성 check가 가능하도록 분할하였는가?
DB 갱신 연산 시 함수 종속성 만족 여부 검사
정의
- F: 테이블 R에 대한 함수 종속성 집합
- R1, R2, ..., Rn: R의 분할
- Fi: Ri에 포함된 필드로만 구성된 함수 종속성 집합
- F' = F1 ⋃ F2 ⋃ ... ⋃ Fn
- F'⁺ = F⁺이면 종속성 보전 분할

📌 정규화(Normalization)

정규형(Normal Form): Relation이 갖는 제약 조건에 따라 분류
정규화: 문제점(데이터 중복, 삽입/삭제/갱신 이상현상)이 있는 Relation 분할하는 과정 (단, 정보 손실 없도록 무손실 조인 분할 & 종속성 보전 분할)
고려 사항: 분할된 각 Relation에 어떤 속성을 할당할 것인가?

🟡 정규형

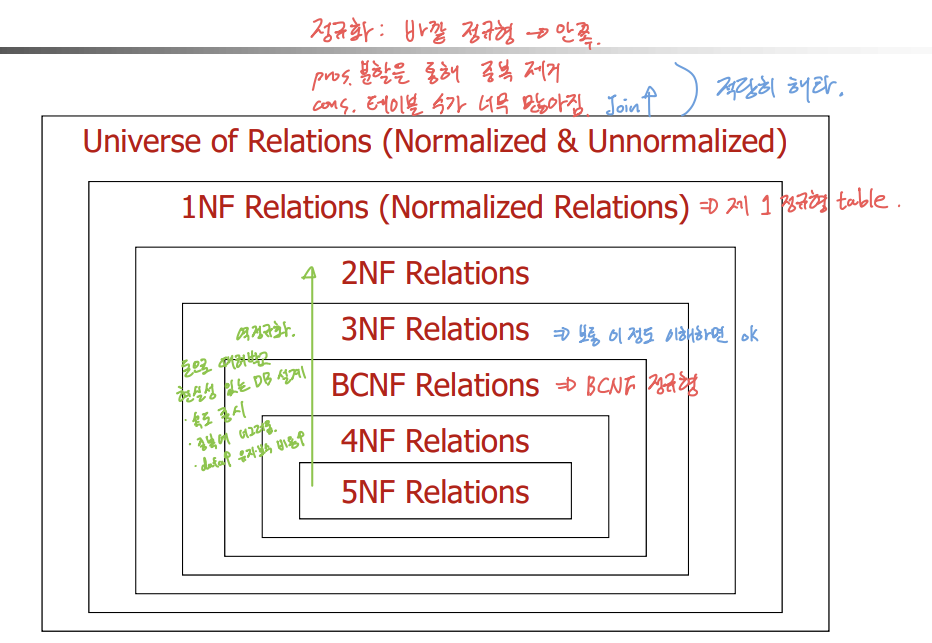
정규화 많이 한다고 꼭 좋은 거 아니다. (테이블 수가 증가해서, Join 수 증가 ⇒ 성능 저하)
그렇다고 너무 안 하면, 데이터 쌓여갈 수록 유지보수 최악

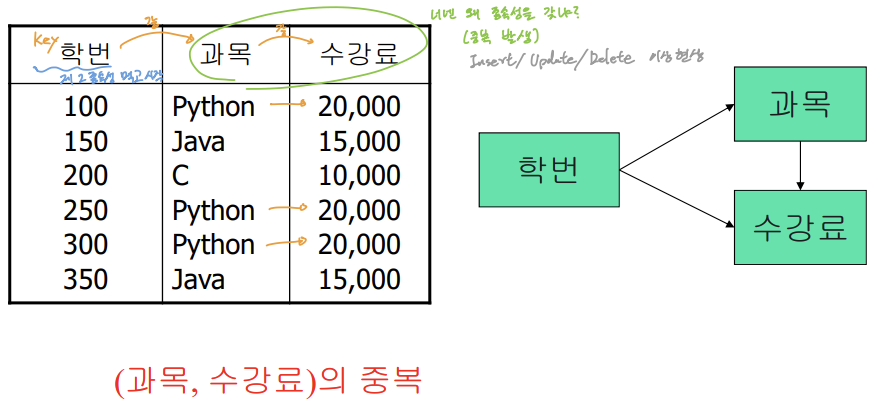
📌 제 1 정규형(First Normal Form: 1NF)

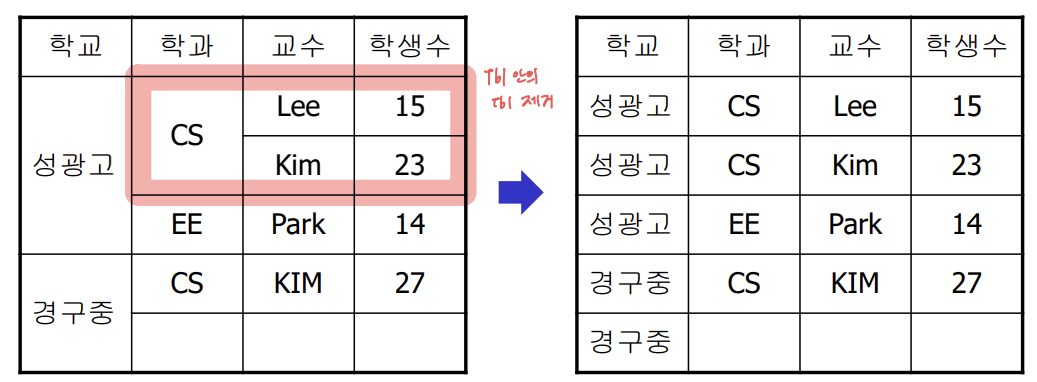
모든 속성들이 원자 값(atomic value)만을 갖는 경우
부분 종속성이 존재한다는 문제가 있다.

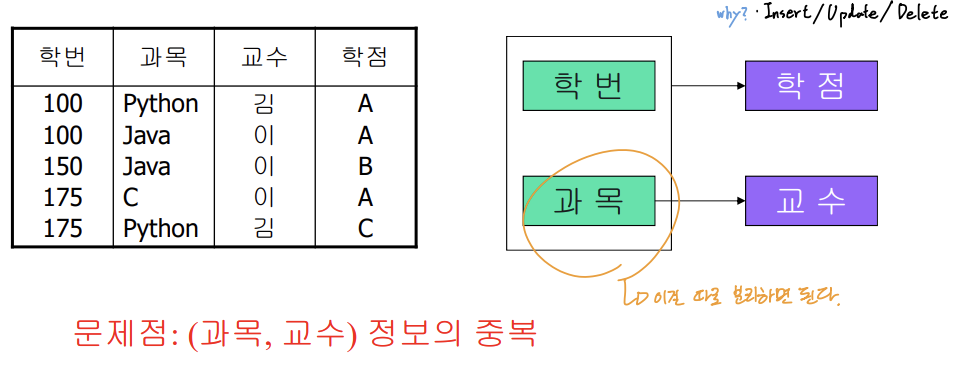
📌 제 2 정규형(Second Normal Form: 2NF)

제 1정규형이며, 주 키에 속하지 않은 모든 속성이 주 키에 완전 종속(부분 종속이 아닌)인 릴레이션
종속성 α→β는 아래 중 하나에 해당한다.
- 단순 종속성
- α가 R의 슈퍼 키
- α가 어떤 후보 키에도 포함되지 않는 속성
- β가 주 키에 포함되는 속성
제 2 정규형으로 무손실 조인 분할 방법 (만약, 속성 하나만 key라면 제 2정규화 먹고 들어가는 것)
- α→β일 때, α⊂P(P: 주 키에 포함되는 속성들의 집합) and β⊄P라고 가정
- R을 R1 = (α, β)과 R2 = (R - β)로 분할 (β를 별도로 빼내자!)
이행 종속성이 존재한다.

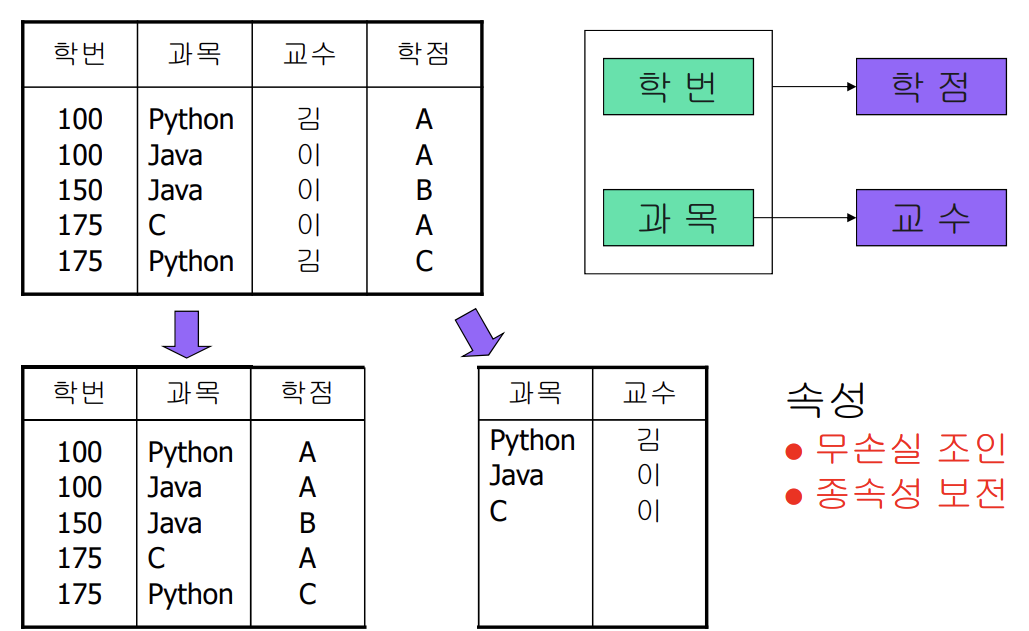
📌 제 3 정규형(Third Normal Form: 3NF)

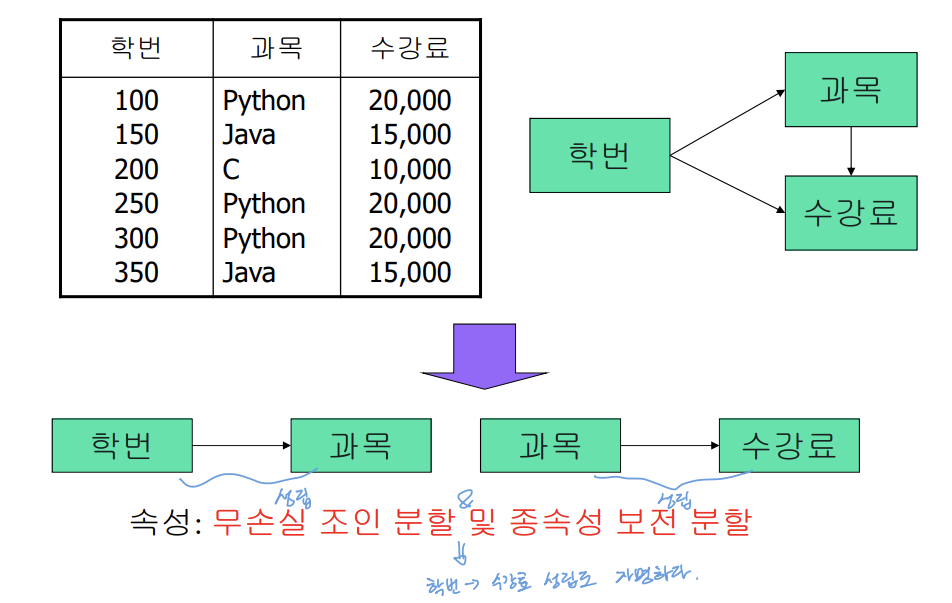
제 2정규형이면서, 주 키에 속하지 않는 모든 속성이 주 키에 이행적 함수 종속이 아닌 릴레이션
종속성 α→β는 아래 중에 하나에 해당한다.
- 단순 종속성
- α가 R의 슈퍼 키
- β가 주 키에 포함되는 속성
제 3정규형으로 무손실 조인 분할 방법
- α→β일 때, α가 R에 대한 슈퍼 키가 아니며, β가 후보키를 포함하지 않는 경우
- R을 R1 = (α, β)과 R2 = (R - β)로 분할
주 키에 포함되지 않는 속성에서 주 키의 일부 속성으로 함수 종속성이 존재할 경우 문제가 발생

📌 보이스-코드 정규형(Boyce-Codd Normal Form: BCNF)

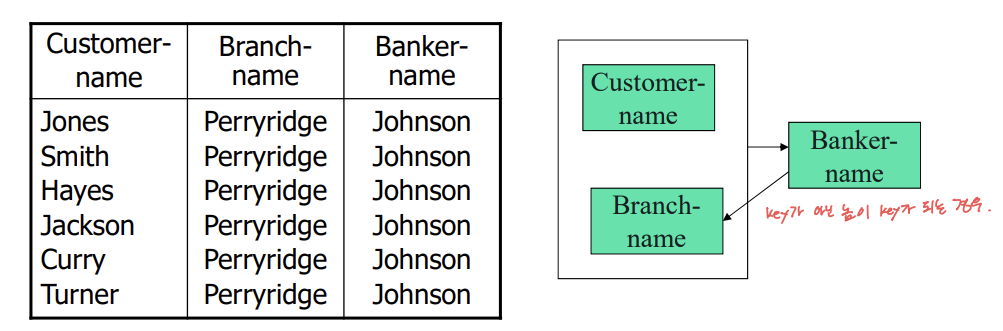
모든 함수 종속성의 결정자(왼쪽 속성)는 후보키 (key가 아닌 놈들은 모두 조각내버리는 전략)
종속성 α→β는 아래 중에 하나에 속한다.
- 단순 종속성
- α가 R의 슈퍼키
BCNF로 무손실 조인 방법
- non-trivial dependency α→β, α가 R의 슈퍼 키가 아닌 경우
- R을 R1 = (α, β)과 R2 = (R - β)로 분리
무손실 조인 분할은 맞지만, 언제나 종속성 보전 분할은 아니다.

📌 정규화 선택 기준

가장 좋은 경우: BCNF이면서 무손실 조인 분할 & 종속성 보존
차선: 3NF에서 무손실 조인 분할 & 종속성 보존

5. 다중치 종속성을 이용한 정규화

제 4 정규화 찍먹

📌 다중치 종속성(Multivalued Dependency)

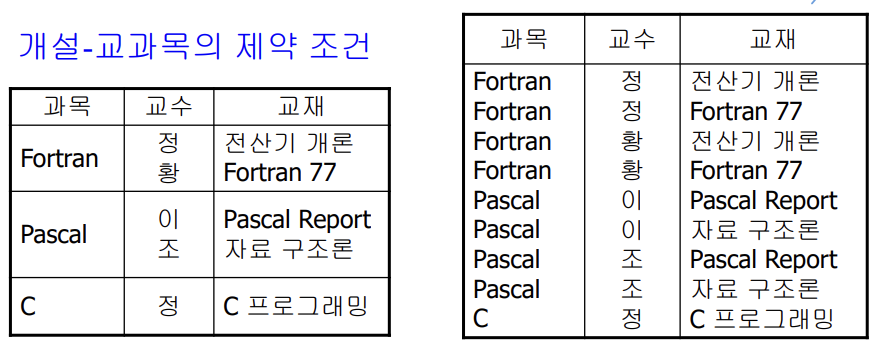
α값에 따라 β값의 종류가 결정
β값이 단 하나로 결정될 경우: Functional Dependency
β값이 하나는 아니지만, α값에 따라 종류가 한정되어 있는 경우 ⇒ 이것조차 분리하자! (비현실적)

저작자표시 비영리

1. 관계형 데이터베이스 설계의 문제점

2. 분할

3. 함수 종속성

4. 함수 종속성을 이용한 정규화

5. 다중치 종속성을 이용한 정규화

티스토리툴바