어느정도 이해했다고 생각했는데 더닝-크루거 효과대로 멍청함의 피크를 찍고 절망의 늪에서 허우적 거리는 중이다.
그래도 지금까지 공부한 부분이라도 포스팅 해야지.
수학적 증명과 물리적 설명을 동반하면서 설명할 거라 내용이 좀 오락가락할 수도 있다.
그리고 푸리에 해석을 위해 베이스로 알아야 하는 많은 개념들(맥클로린 급수, 오일러 공식 등)은 따로 다루어야 할 정도로 중요한 내용이지만, 내게 시간적 여유가 그리 많지 않은 관계로 해당 내용은 추후 따로 정리하도록 하고 여기선 간단하게 알아두어야 할 내용들을 요약해두고 바로 넘어갈 것이다.
참고로 티스토리는 수식을 입력하기 위해
이런 식으로 LaTex 문법을 써야하는 관계로...쓰다가 오타가 났을 가능성이 있다.
[C++] 1067 - 이동 (플래티넘1) : FFT(고속 푸리에 변환)
1. 문제 설명 1067번: 이동 N개의 수가 있는 X와 Y가 있다. 이때 X나 Y를 순환 이동시킬 수 있다. 순환 이동이란 마지막 원소를 제거하고 그 수를 맨 앞으로 다시 삽입하는 것을 말한다. 예를 들어, {1,
jaeseo0519.tistory.com
Fast Fourier Transform(FFT)에 대해서는 다시 수학적 증명을 통해 다룰 것이지만 혹시 궁금한 사람이 있으면 지난 포스팅을 참조하면 된다.
목차
1. Base Concept
① Signal elements
② Series & Trigonometric Series(Furier Series)
③ Angular Velocity(ω)
④ Complex plan
⑤ Euler fommula
⑥ Simple wave
2. Fourier Analysis
3. Relationship Fourier coefficients with Odd/Even function
4. Fourier Physical Analysis
1. Base Concept
우선, 푸리에의 해석을 수학적으로 증명을 해내기 위해선 정말 저엉~말 많은 개념들을 기본으로 깔고 가야한다.
그런데 내가 여기서 맥클로린 급수부터 라플라스 형변환까지 설명하려면 포스팅을 한 10개 정도로 분리해야 하는데
그냥 모르겠으면 다른 블로그를 참조해서 오거나 공업 수학과 선형 대수학을 배운 사람이라면 본인의 예전 노트 필기들을 잘 찾아보면 된다.
참고로 지난 이틀간 독학으로 팠던 내용들이라 틀린 내용이 다소 있을 수 있다.
① Signal elements
Wave(파동)은 곧 Signal(신호)로써 해석될 수 있다.
Signal의 요소는 Amplitute(진폭), period(주기), frequency(주파수), phase(위상) 정도로 나눌 수 있다.
- Amplitute [V or W]
- Period [s]
- Frequency [rad/s or Hz]
- Phase [rad]
위의 이미지는 Sin signal이 1초동안 3번 반복하고 있다. (== 위상이 3rad만큼 회전했다.)
따라서 주파수가 3Hz이고, 주기가 1/3s라고 해석하면 된다.
② Series & Trigonometric Series(Furier Series)
Series(급수)는 수열들의 합이다.
그 중에서 Fourier Series라고도 불리는 Trigonometric Series(삼각 급수)가 있는데 기본적인 몇 가지만 알아보자.
이해하려면 맥클로린 급수에 대해 공부하면 된다.
기본적인 Trigonometric System
1) \( sinx = x - \frac{1}{3!}x^{3} + \frac{1}{5!}x^{5} - \frac{1}{7!}x^{7} + \cdots \)
2) \( cosx = 1 - \frac{1}{2!}x^{2} + \frac{1}{4!}x^{4} - \frac{1}{6!}x^{6} + \cdots \)
3) \( tan^{-1}x = \int \frac{1}{1+x^{2}} = x - \frac{1}{3}x^{3} + \frac{1}{5}x^{5} - \frac{1}{7}x^{7} + \cdots \)
4) \( sinhx = x + \frac{1}{3!}x^{3} + \frac{1}{5!}x^{5} + \frac{1}{7!}x^{7} + \cdots \)
5) \( coshx = 1 + \frac{1}{2!}x^{2} + \frac{1}{4!}x^{4} + \frac{1}{6!}x^{6} + \cdots \)
6) \( \frac{\pi}{4} = \sum_{n=0}^{\infty }\frac{(-1)^{n}}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \)
7) \( arccosx = \frac{\pi}{2} - arcsinx = \frac{\pi}{2} - \sum_{\infty}^{n=0}\frac{(2n)!}{4^{n}(n!)^{2}(2n+1)}x^{2n+1} \)
8) \( e^{x} = 1 + x + \frac{1}{2!}x^{2} + \frac{1}{3!}x^{3} + \cdots = \sum_{n=0}^{\infty}\frac{1}{n!}x^{n} \)
급수해의 존재 정리에 의하면 2계 선형 미분 방정식 \( y'' + p(x)y' + g(x)'y = r(x) \)에서 계수 \( p(x), g(x), r(x) \)가 해석적(\( x=x_{0}=0 \)처럼 멱급수 전개가 된다면)이면, \( f(x) = \sum_{n=0}^{\infty}C_{n}(x_{n} - x_{0})^{n} \)꼴의 일차 독립인 두 급수해가 존재한다.
어쨌든, 삼각함수를 또 모아서 하나의 급수로 만들면 다음처럼 표현 가능하다.
$$ a_{0} + a_{1}cosx + b_{1}sinx + a_{2}cos2x + b_{2}sin2x + \cdots = a_{0} + \sum_{n=1}^{\infty}(a_{n}cosnx + b_{n}sinnx) $$
이 때, a0, an, bn은 상수 취급하면 되고, 이 식이 가지는 의미는 "주기 함수를 지수 함수의 조합으로 표현했다"정도만 이해하고 넘어가자.
③ Angular Velocity(ω)
원 운동을 하고 있는 물체에 일정 속력의 빛을 쏴주면 생기는 그림자가 직선 운동을 할 때와 운동량이 같다.
- \( \theta = \frac{l}{r}[rad] \)
- \( \theta = \omega t = 2\pi f t \; (f=\frac{1}{T},\; T=period) \)
- \( \omega = \frac{\theta}{t} = 2\pi f \)
④ Complex plan
이 분야를 공부하다보면 Complex plan(복소 평면)이란 게 계속해서 나오는데 어지간히 복잡하다.
허수(i)에 대해서 먼저 설명을 해야하는데, 허수란 고등학교 과정에서 "상상의 수"라고 배우지만 그렇다고 없는 값을 만들어 냈다는 것은 아니다. \( i= \sqrt{-1} \)
1700년대까지만 해도 일반해의 값이 음수가 나오면 취급할 필요가 없는 값으로 여겼지만, "더했을 때 0보다 더 작은 수가 있다."라는 개념이 정립이 되면서 수학자들은 일차원 벡터의 의미를 이해할 수 있게 되었다.
하지만 허수란 무엇인가? 두 수를 곱했을 때, 음수가 나온다. 즉, 이번에는 "곱했을 때 0보다 더 작은 수가 있다."라는 뜻인데 21세기까지도 이 개념은 제대로 받아들여지지 않았다.
하지만 음수값을 처음 발견했을 때, 어떻게 해석했었던가? 1차원 벡터로써 값을 표현할 수 있게 되었다고 했다.
즉, 이번에는 2차원 공간인 복소수 영역으로 개념이 확장되기 시작했다.
기존의 x축 y축으로 표현되던 공간상에서 root2를 표현해보라고 한다면 어떻게 할 것인가? 2^(-1)은 또 무슨 의미로 해석할 수 있는가? 2^(1/2)는?
해답은 허수에서 찾아낼 수 있다. 정의를 확장시키면 되는 것이다.
\( 2^{x+y}=2^{x}2^{y} \)임은 자명한 사실이다.
\( 2^{x+y} \)를 Add inputs라 하고, \( 2^{x}2^{y} \)를 Multiply outputs라 한다면, 복소수 평면내에서 Additive group과 Multiplicative group으로 영역을 나누어서 생각해보면 된다.
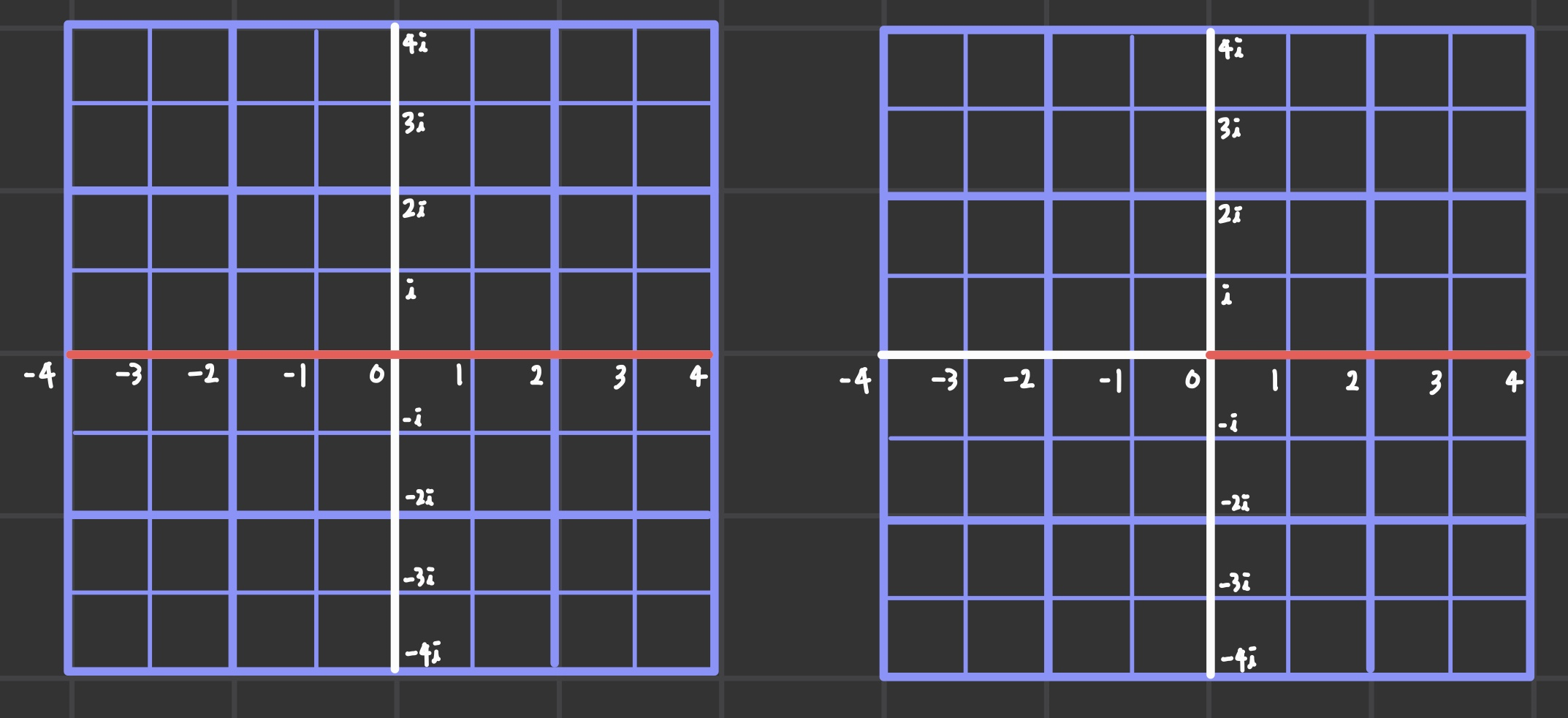
복소수 영역은 해당 값의 phase를 알기 위해 사용한다. 2^x을 생각해보자.
각각의 영역에서 실수부는 붉은색 직선을 의미한다. x는 양과 음의 구간에서 움직일 때, 2^x의 real part가 positive 내에서 움직이는 것은 명백하다.
Additive group에서는 stretching action을 통해 움직이고, Multiplicative group에선 squishing action으로 움직인다.
내가 표시를 해두는 걸 잊어먹었는데, Additive group의 0에 점이 찍혀있다면 Multiplicative group에선 1에 찍혀있을 것이다.
점을 -1로 옮긴다면, Multiplicative group은 squishing action으로 점을 1/2 위치로 옮겨놓게 된다.
그런데 Additive group에서 원점의 위치를 i로 옮긴다면..Multiplicative group은 어떻게 움직이게 될까?
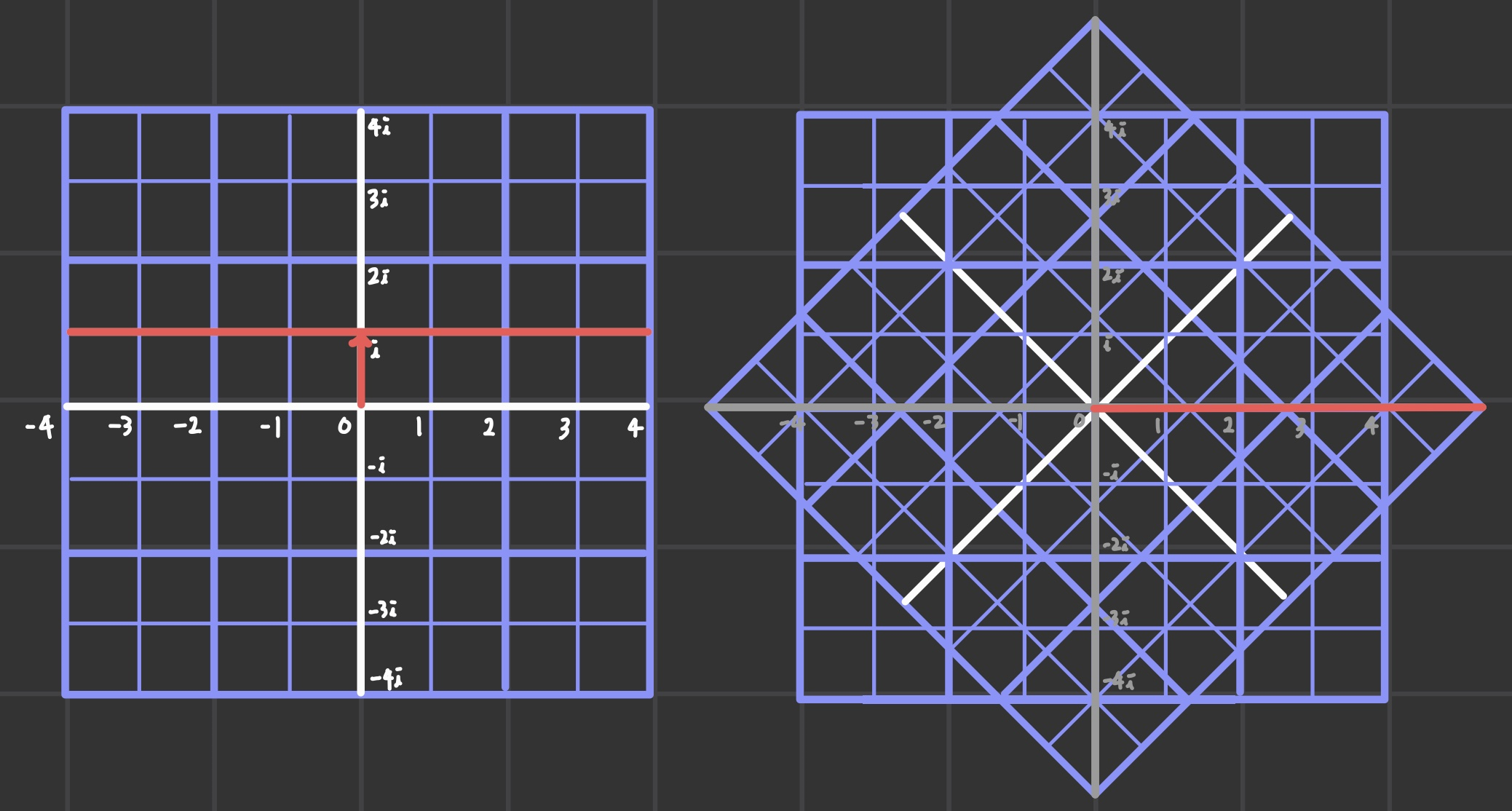
놀랍게도 90도 회전한다. 복소수 i가 의미하는 바는 바로 이것이다.
x=i는 90도 회전변환을 의미하며, x=i*i는 180도 회전변환이 된다.
수를 1차원에서 2차원 벡터로 다루게 되었다는 말이 된다!
그렇다면 회전시키기 전에 Multiplicative group의 1에 찍혀있을 때, 90도 회전시키면 2^i의 위치를 표시할 수 있다.
실제로 Additive group의 복소수 축을 Multiplicative group으로 옮기면 Mutiplicative group을 원으로 감싸게 된다.
말로 설명하기엔 한계가 있으니 이 영상을 참조하자.
⑤ Euler fommula
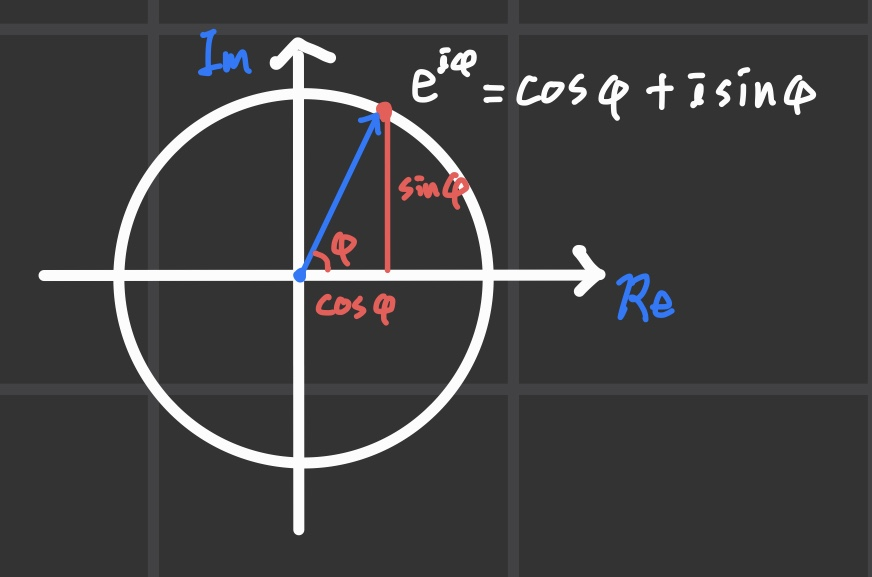
다시 복소수 영역으로 생각해보자. Additive group에 x를 두고, Multiplicative group에서 e^x를 회전시켜보면 된다.
x가 \(i\varphi\)의 값을 가지면 \(e^(i\varphi)\)를 복소수상에서 회전시키면 다음과 같은 공식을 얻을 수 있다.
$$ e^{i\varphi}=cos\varphi + isin\varphi $$
근데 왜 하필이면 많고 많은 값 중에 자연상수를 사용할까?
복소수 좌표 상에서 e^x가 매우 특별한 값을 갖기 때문이다.
하지만 이걸 설명할 만큼 나또한 이해도가 충분하지 않기 때문에 위에 올려둔 영상을 보자.
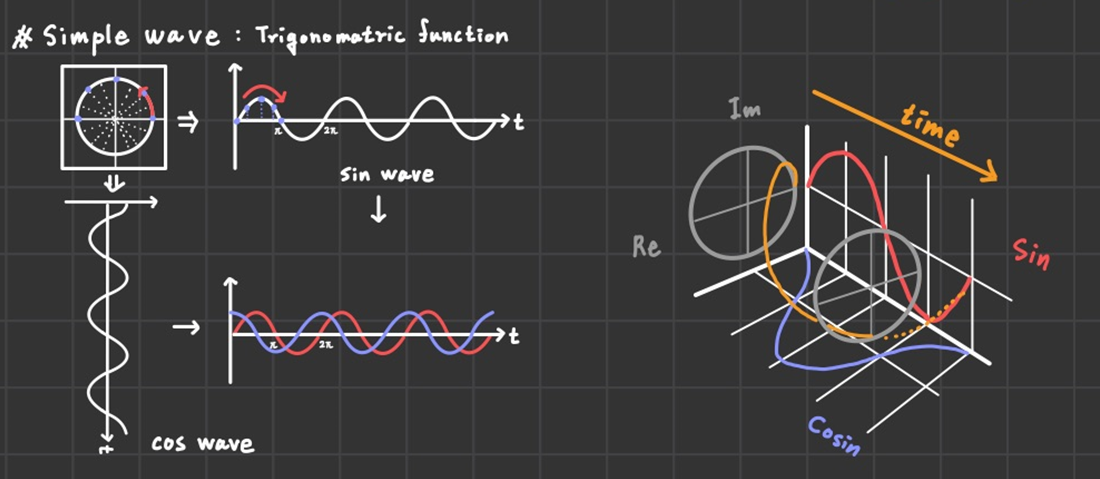
⑥ Simple wave
쉽게 말해서 삼각함수다. 단위는 sinx라고 보면 된다. (cosx도 결국 sinx의 phase를 바꿔서 나온 값이므로)
2. Fourier Analysis
푸리에의 발견은 하나의 의문으로 시작된다.
예를 들어, 여러가지 색이 섞인 물감통이 있다고 가정하자. 이 물감들을 각각의 물감들로 다시 복구할 수 있을까?
당연한 이야기지만 가능했으니까 수많은 공학도들이 푸리에 때문에 머리를 쥐어 뜯으며 살고 있다.
이미지는 현재 시간에 대한 진폭 신호를 표현하고 있는데, Fouriere Transform을 통해 주파수에 대한 진폭 그래프로 바꿀 수 있다.
즉, 시간 도메인에서 주파수 도메인으로 끌고 갈 수 있다는 건데 이렇게 하면 Composit Signal(복합 신호)을 단일 신호들로 표현할 수 있게 된다.
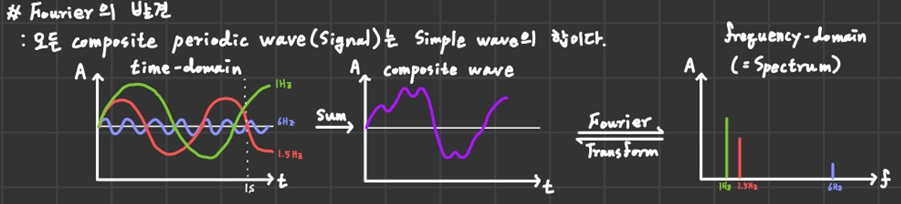
여러 파형(각각의 물감)들이 혼합되면 당연히 파형이 일그러지게 되고, 이는 간섭 효과로 인해 Composite wave(복합 파형, 여러 물감이 섞인 물통)을 이루게 된다.
그런데 이걸 푸리에 변환을 하면 모두 분리할 수 있게 된다. (어케 했누)
Trigonometric Series가 주기 함수를 지수 합수의 조합으로 표현했다면, Fourier 해석을 통해 주기 함수를 지수 함수로 표현 가능하게 된다.
이제 해당 내용을 처음 본 사람들은 아래로 내려갈 수록 혼란과 공포에 빠지게 될 텐데, 반드시 이것 하나만 기억하자.
푸리에의 해석은 결론적으로 아래와 같다.
모든 복합 파동들은 단순한 파동들의 결합으로 이루어진다.대학원에 끌려갈 걸 각오하고 교수님께 질문한 내용의 답변
① Periodic wave는 기본 frequency가 정수배인 주파수들의 파동으로 이루어져 있다.
(복합 파동) = (단순한 파동1) + (단순한 파동2) + (단순한 파동3) + ...
그렇다면 단순한 파동은 어떻게 표현할까?
sinx와 cosx는 Orthogonality(직교성)을 띈다. 참고로 벡터 공간에서 직교한다는 것은 내적이 0임을 의미하고, 두 성분이 독립함을 증명할 수 있는 충분 조건이 된다. 따라서, 직교성을 확인하면 어떤 물리량들을 서로 독립된 특성이라 볼 수 있다.
결국 단순한 파동이란 \( e^{i\varphi}=cos\varphi + isin\varphi \), Euler fomula가 된다.
그렇다면 복잡한 파동을 표현하기 위해 단순한 N개의 파동을 결합하면 되므로 다음의 수식을 유도할 수 있다.
$$ \begin{align} f(t) = a_{0} &+ a_{1}cos\omega t + a_{2}cos2\omega t + \cdots + a_{n}cosn\omega t \\&+ b_{1}sin\omega t + b_{2}sin2\omega t + \cdots + b_{n}sinn\omega t = a_{0} + \sum_{n=1}^{\infty}(a_{n}cosn\omega t + b_{n}sinn\omega t) \end{align} $$
f(x)는 주기함수, a0는 중심축, an, bn은 각각 파동 가중치로써 '주파수 성분이 f에 얼마나 있는가?'를 묻는다고 이해하자.
여기서 ω = 2π⨍t 임을 이용하면 식을 입맛대로 바꿀 수 있다.
주기가 Period이고 범위가 [-L, L]인 f(x)는 다음과 같다.
$$ f(x) = a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(\frac{n\pi x}{L}) + b_{n}sin(\frac{n\pi x}{L})) $$
② a0는 필수적인 존재이다.
sin, cos wave 모두 무조건 0을 중심으로 진동한다고 할 수 없다.
따라서 a0가 중심축이라 했으므로 파동의 중심이 어딘지 알아내야 한다.
③ harmonics 즉, 주기 함수의 각 성분들은 주기 내에서 서로 Orthogonality(직교성)을 갖는다.
harmonics란 고조파라 불리며, 진동 및 소음에서 가장 기본이 되는 기본 주파수를 기준으로 정수배가 되는 성분들을 말한다.
그렇다. ①에서 정의했던 주기 함수에서 가장 기저를 이루는 ω₀일 때를 기본 주파수 성분(1 harmonic)라 한다면,
이 회전수를 2배, 3배 늘린 성분들을 2 harmonic, 3 harmonic, ... 이라고 부른다. (단순 파동1, 단순 파동2, ... 를 떠올리면 된다.)
이는 수학적으로 쉽게 증명 가능한 내용이다.
- vector space에서 두 벡터 u1, u2가 직교성을 띄면 내적이 0이다.
- function space에서 두 함수 f, g가 닫힌 구간 [a, b]에서 직교성을 띄면(독립이면) \( \int_{a}^{b}f(x)g(x)dx \)이다.
이 두 가지 정의를 합하면 간단하게 다음과 같은 식을 유도할 수 있다.
$$ f\cdot g = \int_{a}^{b}f(x)g(x)dx $$
따라서 정의에 의해, 자기 자신과 내적하는 경우를 제외하면 모든 성분은 내적의 값이 0이므로
\( \int_{0}^{T} sin(n\omega x)cos(m\omega x)dx = 0\)
\( \int_{0}^{T} sin(n\omega x)cos(m\omega x)dx = 0\) (단, n ≠ m)
\( \int_{0}^{T} sin(n\omega x)cos(m\omega x)dx = 0\) (단, n ≠ m)
세 가지 결과를 유도해낼 수 있다. 좀 더 이해하기 쉽게 그래프로 나타내보자.
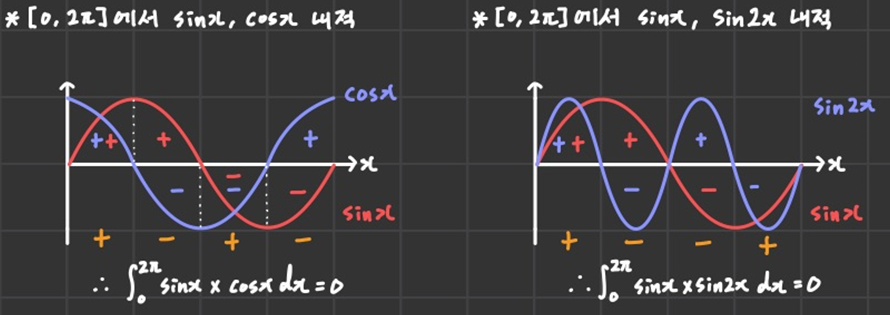
어차피 진폭의 크기는 같으니 부호만 판단해주어도 충분하다.
서로 다른 두 성분은 제 아무리 경우의 수를 찾아봐도 주기 내에서 양의 부호와 음의 부호가 일치한다.
따라서 적분 결과는 0이다.
하지만 동일한 성분을 내적하면 이론적으로도 0이 되는 것은 불가능하다.
좀더 물리학적인 내용으로 들어가면 기존 주파수의 1/2이 되는 주파수가 생성된다.
대충 자기 자신과는 내적의 값이 0이 아닌 것만 알면 된다.
이러한 성질들을 이용하여 Fourier의 주기 함수의 coefficients의 값을 알아낼 수 있다!
여기서 두 단계로 나눌 것인데, 하나는 푸리에 수식을 수학적으로 풀이하여 Fourier Series의 최종적인 형태를 구하는 것과 물리적인 해석법으로 어떤 의미를 갖는지에 대해 설명할 것이다.
3. Relationship Fourier coefficients with Odd/Even function
정의에 의하여 주기 함수 f는 다음과 같이 표현될 수 있다.
$$ f(t) = a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(n\omega t) + b_{n}sin(n\omega t)) $$
구간 [-L, L]에 대하여 period = 2L이라 할 수 있으므로 θ = ωt = 2π⨍t = 2πt/p = πt/L을 이용하면,
$$ f(x) = a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(\frac{n\pi x}{L}) + b_{n}sin(\frac{n\pi x}{L})) $$
두 가지 방법으로 정의할 수 있다.
'왜 굳이?'라고 생각할 수 있지만 이제부터 Furier coefficients를 구할 건데 전자의 식으로 하면 물리적으로 이해하기가 다소 어렵다.
하지만 일단 복소수 좌표계에서 유도해보자.
1. 복소수 좌표계에서 Fourier coefficients 유도
① a₀(= 중심축) 구하기
삼각함수 정적분 구간이 period라면 정적분 결과는 0이다.
주기 함수는 복합 파장을 의미하고 복합 파장은 곧 simple wave의 총 합으로 이루어져 있다.
그렇다면 전체를 period에 대해 정적분을 해버리면 simple wave는 모두 0이 되므로 a₀만 남게 된다.
$$ \begin{align} \int_{0}^{T}f(t)dt &= \int_{0}^{T}a_{0}dt \\&=Ta_{0} \end{align} $$
$$ \therefore a_{0} = \frac{1}{T}\int_{0}^{T}f(t)dt = \frac{1}{2L}\int_{-L}^{L}f(x)dx $$
② an, bn (f의 주파수 성분 가중치) 구하기
주기 함수의 직교성으로 인해 자기 자신을 내적하는 경우를 제외하면 모두 0이 된다.
1) an → f(t)에 cos(nωt)를 곱하고 주기로 적분
$$ \begin{align} \int_{0}^{T}f(t)cos(n\omega t)dt &= \int_{0}^{T}cos(n\omega t)a_{0}dt + \sum_{n=1}^{\infty}(\int_{0}^{T}cos(n\omega t)cos(n\omega t)dt + b_{n}\int_{0}^{T}cos(n\omega t)sin(n\omega t)dt) \\&= \sum_{n=1}^{\infty}(a_{n}\int_{0}^{T}cos(n\omega t)cos(n\omega t)dt) \\&= a_{n}\sum_{n=1}^{\infty}(\int_{0}^{T}\frac{1+cos(2n\omega t)}{2}dt) \;\;\;\;\; \because cos(A+B) = \frac{1}{2} (cos(A+B) - cos(A-B)) \\&=\frac{T}{2}a_{n} \end{align} $$
$$ \therefore a_{n}=\frac{2}{T}\int_{0}^{T}f(t)cos(n\omega t)dt = \frac{1}{L}\int_{-L}^{L}f(x)cos(\frac{n\pi x}{L})dx $$
2) bn → f(t)에 sin(nωt)를 곱하고 주기로 적분
$$ \begin{align} \int_{0}^{T}f(t)sin(n\omega t)dt &= \int_{0}^{T}sin(n\omega t)a_{0}dt + \sum_{n=1}^{\infty}(\int_{0}^{T}sin(n\omega t)cos(n\omega t)dt + b_{n}\int_{0}^{T}sin(n\omega t)sin(n\omega t)dt) \\&= \sum_{n=1}^{\infty}(b_{n}\int_{0}^{T}sin(n\omega t)sin(n\omega t)dt) \\&= b_{n}\sum_{n=1}^{\infty}(\int_{0}^{T}\frac{1-cos(2n\omega t)}{2}dt) \;\;\;\;\; \because sin^{2}x = \frac{1}{2} (1 - cos(2x)) \\&=\frac{T}{2}b_{n} \end{align} $$
$$ \therefore b_{n}=\frac{2}{T}\int_{0}^{T}f(t)sin(n\omega t)dt = \frac{1}{L}\int_{-L}^{L}f(x)sin(\frac{n\pi x}{L})dx $$
개인적으로 공부할 때 썼던 건데 보기 더 편한 걸 참고하면 된다.
an은 cos wave의 가중치이고, bn은 sin wave의 가중치였으므로 동의를 하든 못 하든 수학적인 측면으로는 아무런 문제가 없음이 입증되었다.
하지만 문제는 a0, an, bn의 값을 구하긴 했는데 이 과정이 대체 어떤 물리적 의미를 갖는 걸까?
이 부분에 대해서는 문제를 직교 좌표계 영역으로 끌고와서 풀어보는 것이 훨씬 이해하기 쉽다. (내 기준 ㅎ)
2. 직교 좌표계에서 Fourier coefficients 사용
우선 직교 좌표계에서 복합 파형의 정의는 다음과 같다.
$$ f(x) = a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(\frac{n\pi}{L}) + b_{n}sin(\frac{n\pi}{L}) $$
이제 f 함수를 짝수항과 홀수항에 대해 분리하여 생각해보자.
# Periodic Rectangle Wave
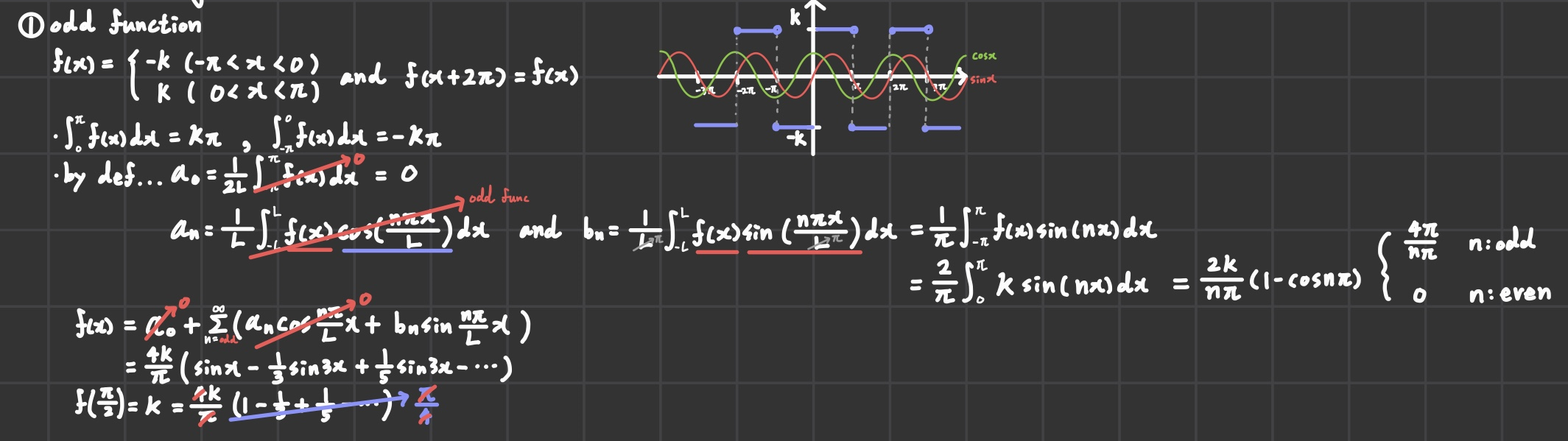
① odd function
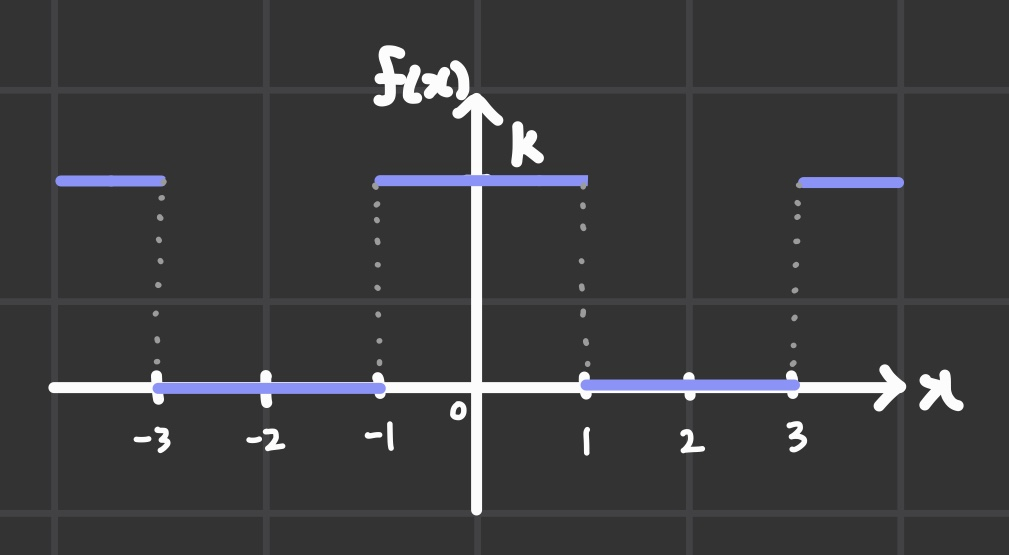
f(x)를 다음과 같이 정의했을 때,
$$f(x) = \left\{\begin{matrix}
-k \;(-\pi < x < 0)
\\k \;(0 < x < \pi)
\end{matrix}\right. \; and \; f(x + 2\pi) = f(x)$$
f(x) 그래프는 위의 이미지처럼 표현될 수 있다.
f(x)는 복합파형이므로 이론적으로는 이를 단순 파형의 합으로 표현가능한데 직접 확인해보면 된다.
$$ \int_{0}^{\pi}f(x)dx = k\pi , \int_{-\pi}^{0}f(x)dx = -k\pi $$
이므로 정의에 의해
$$ by \; def \cdots a_{0}=\frac{1}{2L}\int_{-\pi}^{\pi}f(\pi)dx = 0 $$
주기 함수를 주기에 대해 적분하였으므로 a0는 0이 된다.
$$ a_{n} = \frac{1}{L}\int_{-L}^{L}f(x)cos(\frac{n\pi x}{L})dx = 0 $$
여기선 f(x)가 기함수, cos식은 우함수이므로 기함수*우함수=기함수가 되어 주기에 대해 적분을 하면 0이 된다.
$$ \begin{align} b_{n} = \frac{1}{L}\int_{-L}^{L}f(x)sin(\frac{n\pi x}{L})dx &= \frac{1}{\pi}\int_{\pi}^{-\pi}f(x)sin(nx)dx \\&= \frac{2}{\pi}\int_{0}^{\pi}ksin(nx)dx \\&= \frac{2k}{n\pi}(1-cosn\pi) \; \left\{\begin{matrix} \frac{4k}{n\pi}\;(n:odd) \\0\;\;\;(n:even) \end{matrix}\right. \end{align} $$
이므로 최종적으로 주기함수 f(x)를 구할 수 있다.
$$ \begin{align} f(x) &= a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(\frac{n\pi x}{L})+b_{n}sin(\frac{n\pi x}{L})) \\&=\frac{4k}{\pi}(sinx - \frac{1}{3}sin3x + \frac{1}{5}sin5x - \cdots) \end{align} $$
$$ \therefore f(\frac{\pi}{2}) = k = \frac{4k}{\pi}(1-\frac{1}{3}+\frac{1}{5}-\cdots) $$
\( (1-\frac{1}{3}+\frac{1}{5}-\cdots) \)는 \( \frac{\pi}{4} \)에 수렴하므로 위의 수식은 합당하다.
수학적으로는 f(x)가 odd function임을 가정하고 증명하였지만, 이해를 위해서는 역으로 접근하는 것이 편하다.
f(x)가 아니라 simple wave인 sinx, -1/3sin3x, 1/5sin5x, ...가 더해지는 과정을 보자.
이는 현재 sin함수의 홀수항들이 더해졌음을 의미하고 이 결과가 f(x)처럼 rectangle wave를 만들고 있음을 의미한다.
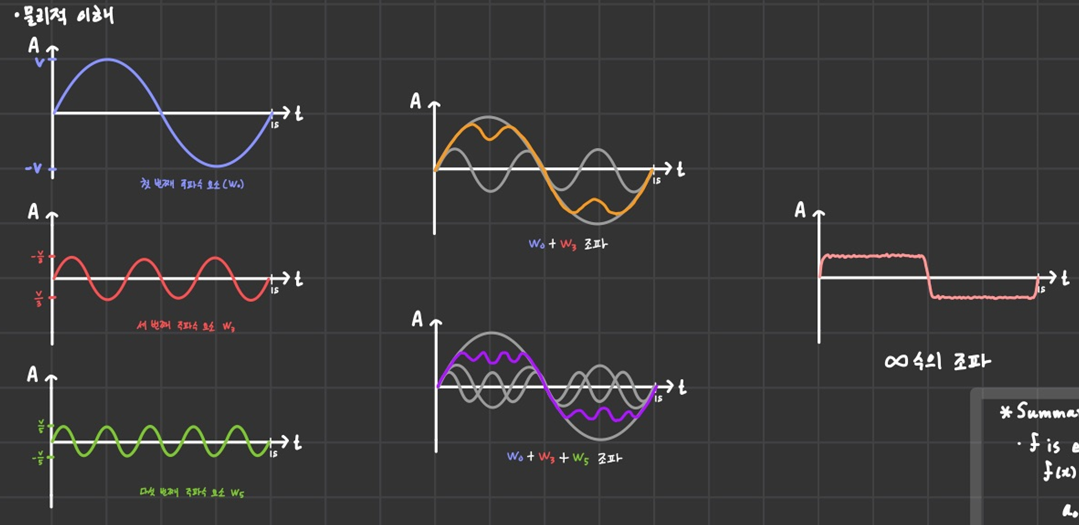
홀수항의 조파를 더하면서 서로 간섭을 유발하고, 최종적으로 무한수의 조파는 가장 오른쪽처럼 이루어진다.
물론 정확한 표현은 아니다. 실제로는 이 과정에서 직각이 되는 부분이 조금씩 튀어나간다.
이건 불연속을 포함하는 파형이 푸리에에 합성되면, 불연속 지점 근처에서 나타나는 불일치 현상으로써 깁스 현상이라고 불리는데 지금은 여기까지 알 필요는 없다.
지금은 그냥 주기적이고 배수적인 단순 조파를 무한대로 보정함으로써 이렇게 f(x)를 만들어낼 수 있구나! 정도만 짚고 넘어가자.
② even function
이번에는 주기 함수 f가 우함수인 경우를 가정해보자.
$$ f(x)=\left\{\begin{matrix}
0\;(-2 < x < -1)
\\k\;(-1 < x < 1)
\\0\;(1 < x < 2)
\end{matrix}\right. \;and\; period=4\;(L=2) $$
그러면 아래와 같은 형태를 가질 것이다.
$$ \begin{align} by \; def \cdots a_{0}=\frac{1}{2L}\int_{-L}^{L}f(x)dx &= \frac{1}{4}\int_{-2}^{2}f(x)dx \\&= \frac{1}{4}\int_{-1}^{1}kdx = \frac{k}{2} \end{align} $$
$$ b_{n} = \frac{1}{L}\int_{-L}^{L}f(x)sin(\frac{n\pi x}{L})dx = 0 $$
이번에는 an이 아니라 bn이 날아감을 알 수 있다.
$$ \begin{align} a_{n} = \frac{1}{L}\int_{-L}^{L}f(x)cos(\frac{n\pi x}{L})dx &= \frac{1}{2}\int_{-1}^{1}kcos(\frac{n\pi x}{L})dx \\&= \frac{2k}{n\pi}sin(\frac{n\pi}{2}) \left\{\begin{matrix} 0 \;\;\; (n\;is\;even) \\ \frac{2k}{n\pi} \; (n=1,5,9,\cdots) \\ \frac{-2k}{n\pi} \; (n=2,7,11,\cdots) \end{matrix}\right. \end{align} $$
$$ \begin{align} f(x) &= a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(\frac{n\pi}{L})x + b_{n}sin(\frac{n\pi}{L})x) \\&= \frac{k}{2} + \frac{2k}{\pi}(cos\frac{\pi}{2}x - \frac{1}{3}cos\frac{3\pi}{2}x + \frac{1}{5}cos\frac{5\pi}{2}x - \cdots ) = \frac{k}{2} \end{align} $$
급수 부분은 0으로 날아가므로 이 또한 합당하다.
③ Summary
| f | odd func | even func |
| a₀ | \( \frac{1}{L}\int_{0}^{L}f(x)dx \) | 0 |
| \(a_{n}\) | \( \frac{2}{L}\int_{0}^{L}f(x)cos(\frac{n\pi x}{L})dx \) (단, n = 1,2,3,...) | 0 |
| \(b_{n}\) | 0 | \(\frac{2}{L}\int_{0}^{L}f(x)sin(\frac{n\pi x}{L})dx\) (단, n = 1,2,3,...) |
| f(x) | \(f(x)=a_{0}+\sum_{n=1}^{\infty}a_{n}cos(\frac{n\pi x}{L}) \) | \(f(x)=\sum_{n=1}^{\infty}b_{n}sin(\frac{n\pi x}{L}) \) |
3. 최종적인 Fourier Series 형태
그냥 값을 다 때려넣으면 된다.
아, 시작하기 전에 Euler fommula는 다시 한 번 짚고 넘어가자.
- \( e^{in\omega t} = cos(n\omega t) + isin(n\omega t) \)
- \( e^{-in\omega t} = cos(n\omega t) - isin(n\omega t) \)
- \( cos(n\omega t) = \frac{1}{2}(e^{in\omega t} + e^{-in\omega t}) \)
- \( sin(n\omega t) = \frac{1}{2i}(e^{in\omega t}-e^{-in\omega t}) \)
① an, bn 정리
\( \begin{align} a_{n}&=\frac{1}{T}\int_{0}^{T}f(t)cos(n\omega t)dt \\&= \frac{1}{T}\int_{0}^{T}(f(t)e^{in\omega t} + f(t)e^{-in\omega t})dt \\&=\frac{1}{T}\int_{0}^{T}f(t)e^{in\omega t}dt + \frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t} dt \end{align} \)
\( \begin{align} b_{n}&=\frac{1}{T}\int_{0}^{T}f(t)sin(n\omega t)dt \\&= \frac{1}{Ti}\int_{0}^{T}(f(t)e^{in\omega t} - f(t)e^{-in\omega t})dt \end{align} \)
\(\begin{align} ib_{n} &= \frac{1}{T}\int_{0}^{T}(f(t)e^{in\omega t} - f(t)e^{-in\omega t})dt \\&= \frac{1}{T}\int_{0}^{T}f(t)e^{in\omega t}dt - \frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t} dt\end{align} \)
식을 잘 조합해보면 다음의 형태를 얻을 수 있다.
$$\frac{1}{2}(a_{n}-ib_{n}) = \frac{1}{T}\int_{0}^{T}e^{in\omega t} = A_{n} $$
$$\frac{1}{2}(a_{n}+ib_{n}) = \frac{1}{T}\int_{0}^{T}e^{-in\omega t} = B_{n}$$
② 푸리에 급수 최종 형태
$$ \begin{align} f(t) &= a_{0} + \sum_{n=1}^{\infty}(a_{n}cos(n\omega t) + b_{n}sin(n\omega t)) \\&= a_{0} + \sum_{n=1}^{\infty} (\frac{a_{n}}{2}(e^{in\omega t} + e^{-in\omega t}) + \frac{b_{n}}{2i}(e^{in\omega t} + e^{-in\omega t})) \\&= a_{0} + \sum_{n=1}^{\infty} (\frac{a_{n}}{2}e^{in\omega t} + \frac{a_{n}}{2}e^{-in\omega t} - \frac{b_{n}}{2i}e^{in\omega t} - \frac{b_{n}}{2i}e^{-in\omega t}) \\&= a_{0} + \frac{1}{2}\sum_{n=1}^{\infty} ((a_{n}-ib_{n})e^{in\omega t} + (a_{n}+ib_{n})e^{-in\omega t}) \\&= \sum_{n=0}^{\infty}A_{n}e^{in\omega t} + \sum_{n=1}^{\infty}B_{n}e^{-in\omega t} \\&= \sum_{n=0}^{\infty}A_{n}e^{in\omega t} + \sum_{n=-1}^{-\infty}B_{n}e^{in\omega t} \\&= \sum_{n=-\infty}^{\infty}C_{n}e^{in\omega t} \end{align} $$
$$ \therefore C_{n}=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t} $$ ⋯ Cn : 성분 개수, f(t) : 복합 파형, e^{-inωt}: n번 째 단일 파동
4. Fourier Physical Analysis
여기까지 오면 한 가지 의문이 들 수 있는데..결국 이렇게 고생을 해서 알아낼 수 있는 게 대체 뭘까?
시작하기 직전에 푸리에는 여러 물감이 섞인 물감을 각각의 색으로 분리할 수 있다고 했는데 어떻게 가능해지는 걸까.
사실 이 부분을 글과 그림으로 어디까지 설명할 수 있을지는 모르겠지만 최대한 노력해보자.
매우 설명이 잘 되어 있는데..? 똑같은 설명을 할 건데 이해가 안 되는 사람만 보자.
근데 영상 퀄리티가 너무 높아서 내 설명은 패스해도 될 것 같다.
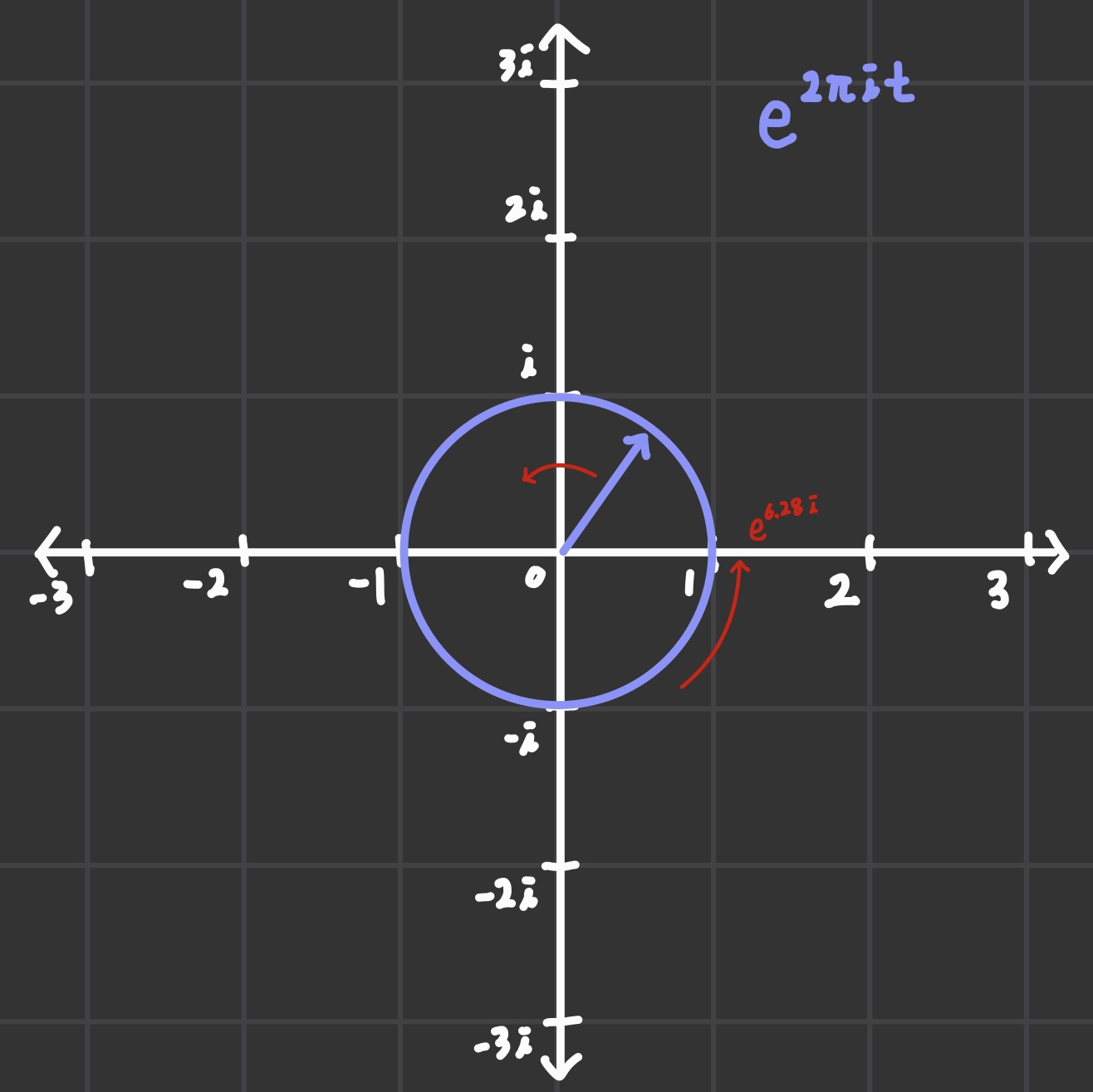
복소수 평면에서 위와 같은 원의 움직임을 \( e^{2\pi it} \)로 정의할 수 있음을 언급했었다.
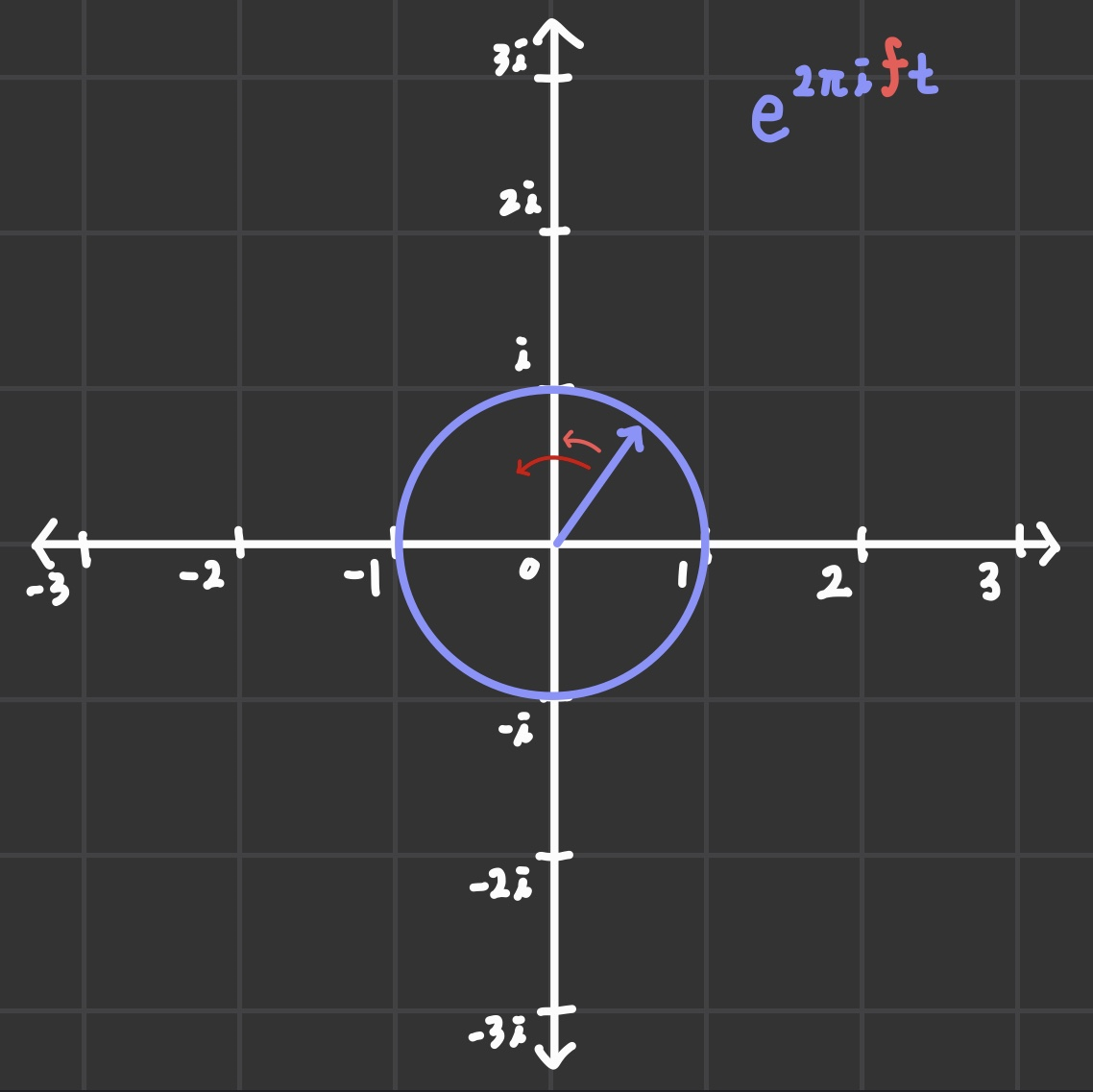
여기에 frequency를 곱해서 회전 속도를 좀 늦춰주고
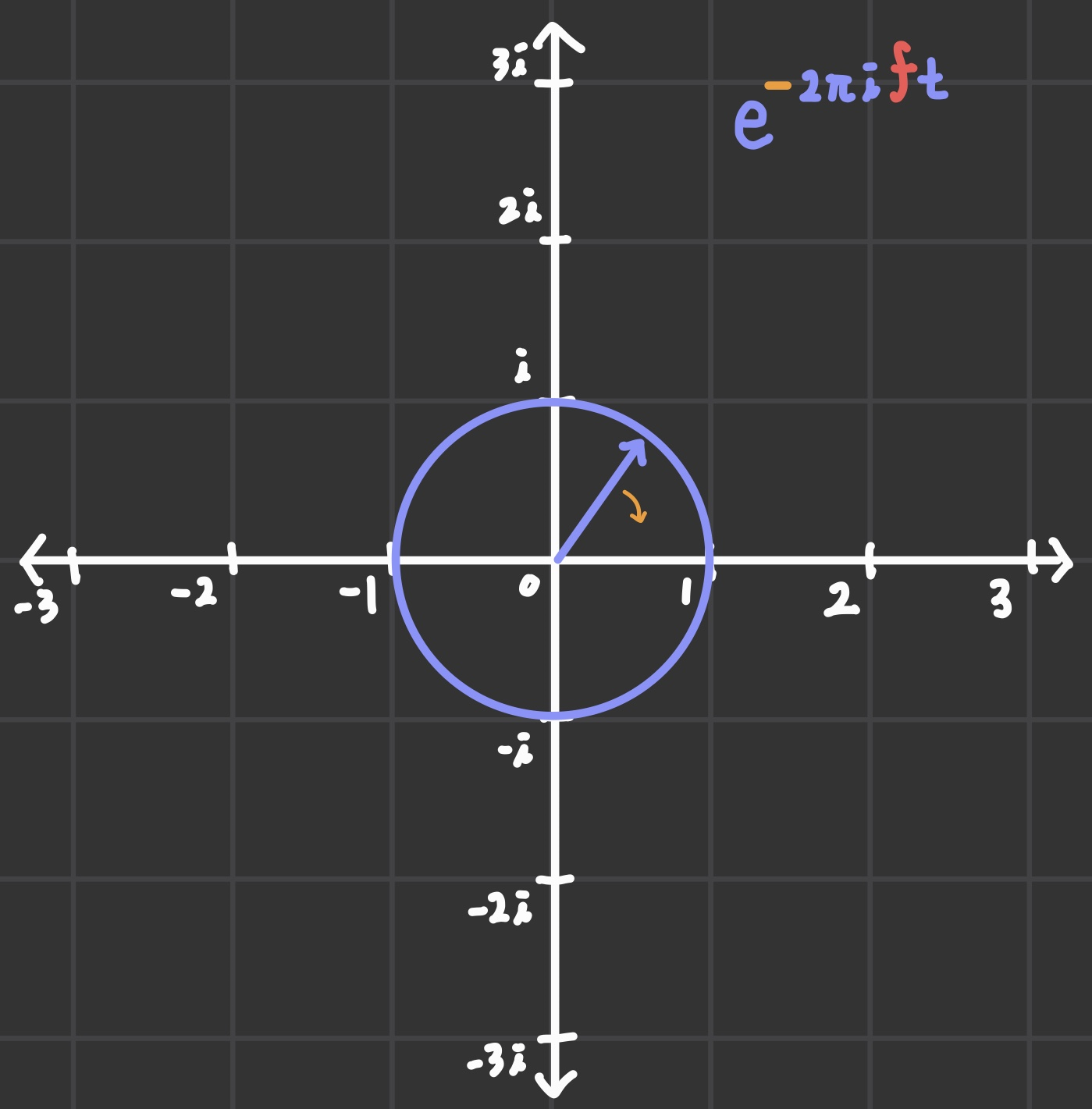
푸리에 해석은 시계 방향으로 회전 시키는 게 관습적이다. (이유가 있긴 한데, 나중에 다루도록 하자.)
따라서 -를 곱하면 복소수 평면 상에서 위의 거동을 표현할 수 있다.
네트워크 분야에는 analog signal을 digtal signal로 표현하기 위해 Sampling이라는 과정을 거치는데, 쉽게 말해 일정 간격으로 점을 찍어서 digital data를 만드는 과정이다.
우린 여기서 조금 개념을 바꾸어 모든 점이 질량을 갖는다고 가정해보는 것이다.
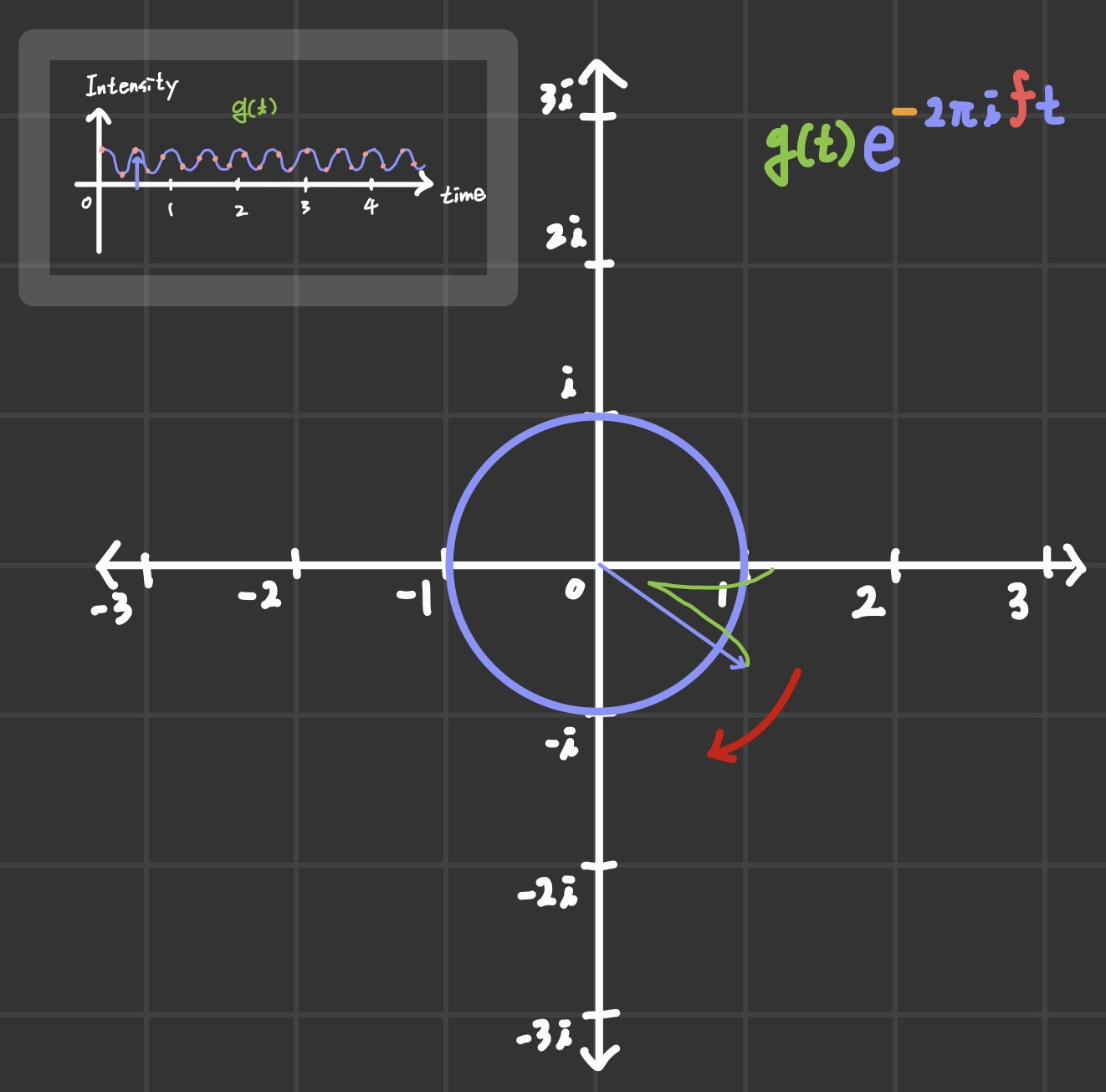
우선 함수 g(t)를 곱하면 복소수 좌표에서 이동 양상은 위의 그림처럼 진행될 것이다.
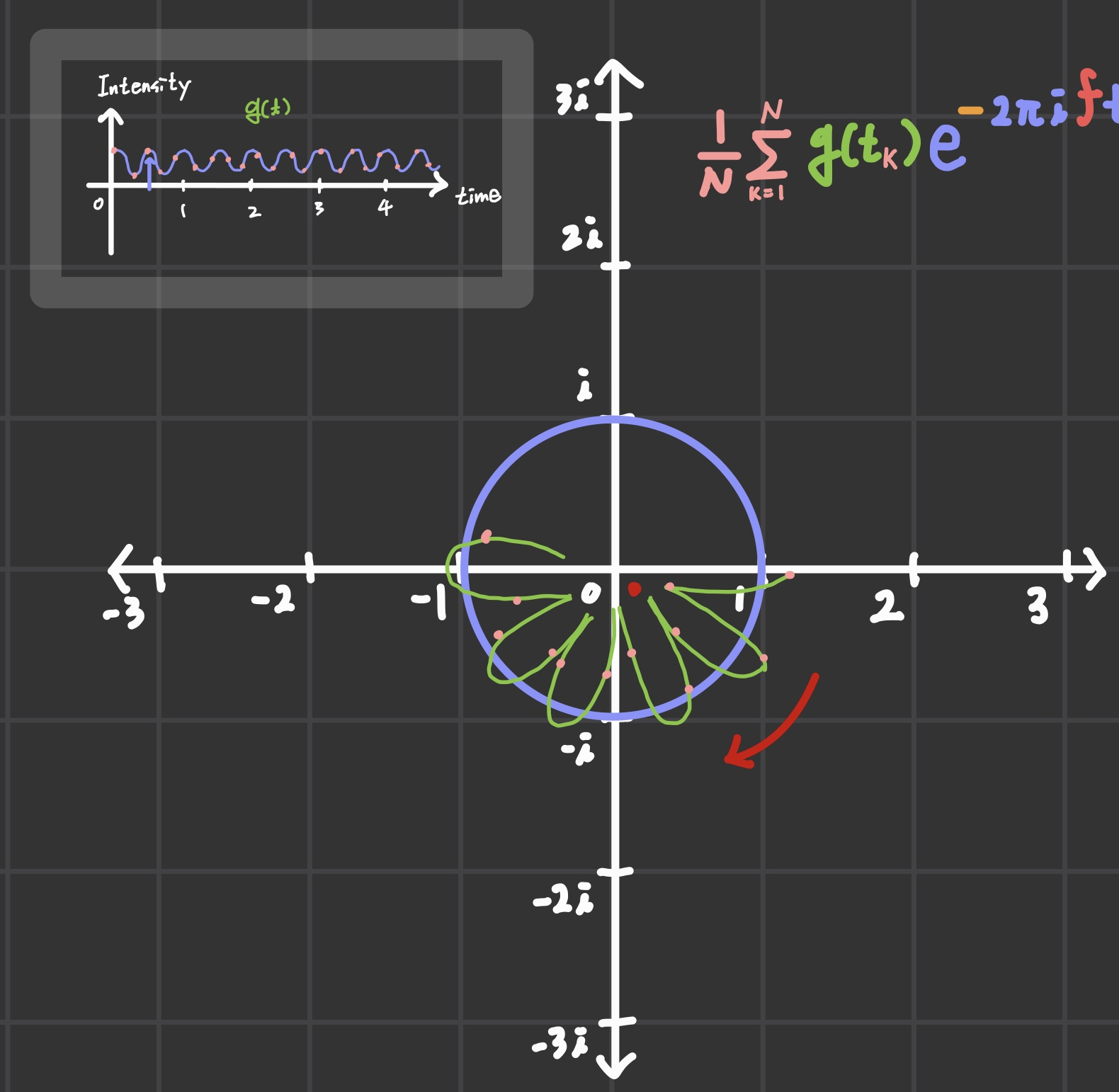
샘플링된 점의 개수만큼 평균치를 구하면 무게 중심이 이동하는 값을 측정할 수 있을 것이다.
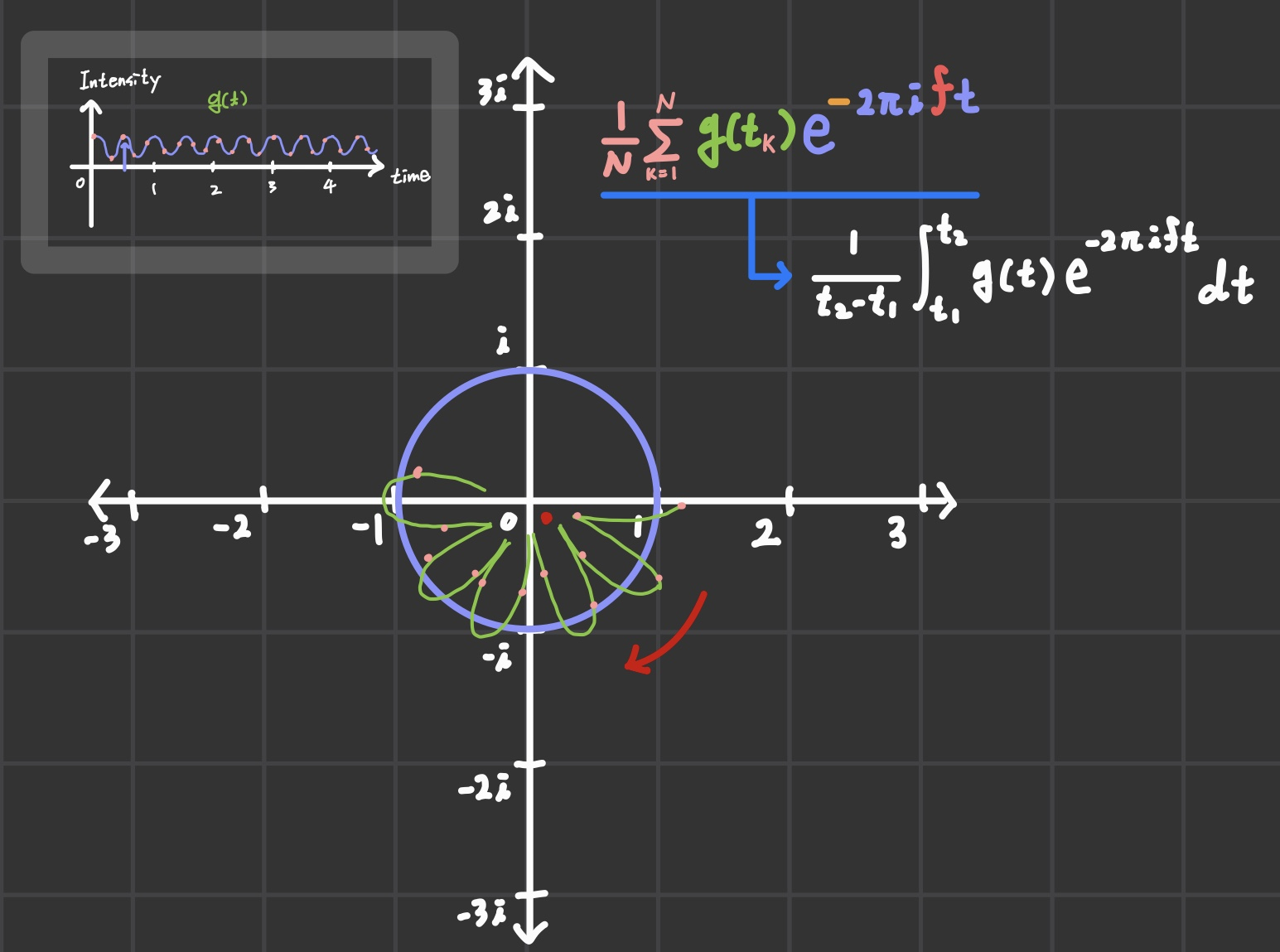
그런데 discrete가 아닌 continuos 영역에 대해선 무한대의 영역에 대해 고려해야 하므로
전체 적분에 대해 시간으로 나누어주면 된다. 어디서 많이 본 식이 나오지 않았나?
바로 최종적으로 구했었던 푸리에 급수의 형태와 동일하다.
$$ C_{n}=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t} $$
초반에 나왔던 그림을 다시 들고오면 복합 신호의 무게 중심을 돌리다 보면 급등하는 지점들이 생기기 마련이다.
바로 composit wave 내의 어떤 simple wave의 주파수와 일치하게 회전하고 있을 때가 그 시점이다.
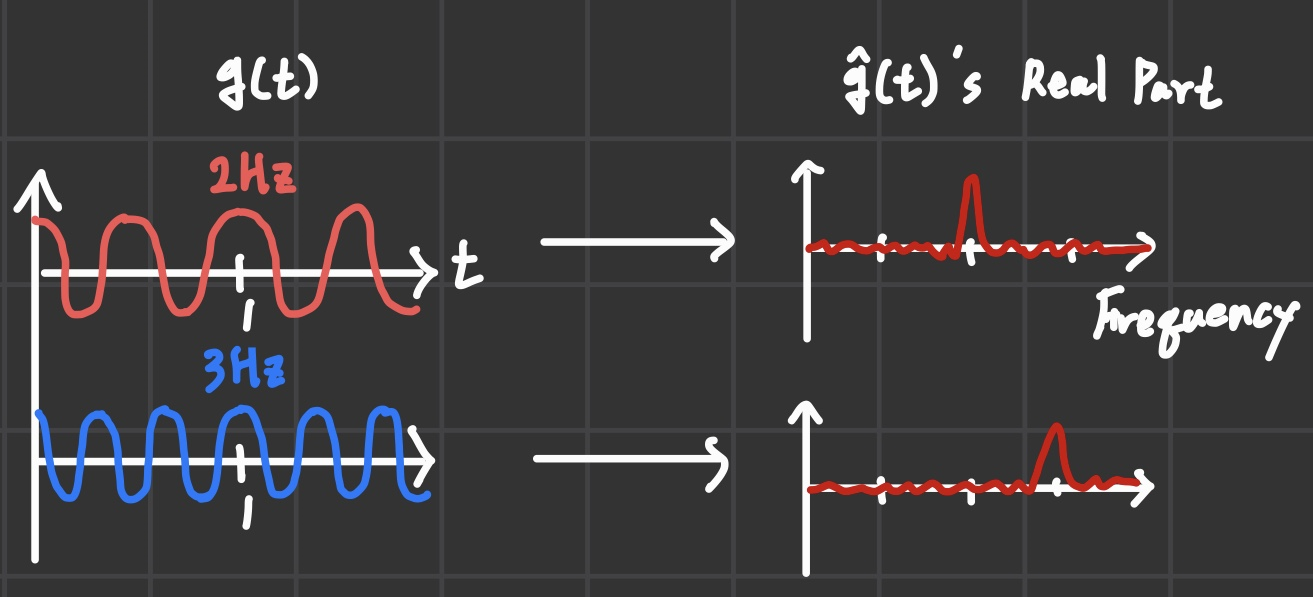
이렇게 하면 특정 주파수 영역대의 파동만 제거해버림으로써 최종적으로 얻고자 하는 파동을 만들어낼 수 있다.
이거 말고도 푸리에 식은 굉장히 다양한 분야에서 쓰일 텐데, 어차피 이 글을 볼 정도로 절박한 공학도라면 조만간 몸소 깨닫게 될 것이다. ㅅㄱㅂ