정말 듣고 싶은 수업이었는데, 복전생이라고 여석 안 열어준 수업..🥲
그래서 청강해도 되는지 여쭤봤었는데, 교수님께서 답을 안 주셔서 '이건 암묵적 허용이다'라는 정신 무장을 하고 들었었던 에피소드가 있다.
진짜 재밌는 내용들이 많았는데, 다시 보니 기억이 가물가물해서 복습할 겸 정리.
📕 목차
1. 보안 목표와 서비스
2. 전통적인 대칭 키 암호화
3. AES (Advanced Encryption Standard)
1. 보안 목표와 서비스
📌 Security Goald
1️⃣ 기밀성(Confidentiality)
- 민감한 정보(sensitive information)가 외부에 노출되는 것을 막자
2️⃣ 무결성(Integrity)
- 정보의 변경은 인가(authorized)된 자에 의해서 인가된 메커니즘을 통해서만 수행될 것
- 악의적인 행동의 결과 또는 시스템 중단과 같은 외부 요인에 의해 침해 가능
3️⃣ 가용성(Availability)
- 조직이 생산하고 저장하는 정보는 인가된 자가 사용할 수 있어야 한다.
- 예를 들어, DDoS 공격으로 일반 사용자가 서비스를 접속할 수 없어서는 안 된다.
📌 Attack
1️⃣ 기밀성을 위협하는 공격
- 스누핑(Snooping): 데이터에 대한 비인가 접근 또는 탈취
- 트래픽 분석(Traffic analysis): 온라인 트래픽을 분석하여 암호화된 메시지 전송의 특성 파악
✒️ Sniffing vs. Snooping vs. Sppfing
• 스니핑(Sniffing): 패킷 가로채기 공격. 네트워크에 떠돌아다니는 패킷이나 데이터를 홈쳐보는 것으로 ICMP 리다이렉트 이용 및 스위치 재밍 등이 있다.
• 스누핑(Snooping): 네트워크 상의 정보를 염탐하여 불법적으로 획득하는 것. 스니핑과 유사
• 스푸핑(Spoofing): 네트워크 트래픽 흐름을 임의로 변경하거나, 시스템 권한기 등의 공격 등. MAC Addr, IP Addr, Port 등 여러가지가 공격 대상이 될 수 있다.
2️⃣ 무결성을 위협하는 공격
- 공격자는 정보를 가로채거나 획득한 후, 자신에게 유리하도록 정보를 조작
- 공격자가 다른 사람으로 위장하거나, 가장 (Spoofing)
- 공격자는 사용자가 보낸 메시지를 획득하고 나중에 해당 메시지를 다시 사용
3️⃣ 가용성을 위협하는 공격
- 서비스 거부(Denial of Service: Dos): 시스템의 서비스를 느리게 하거나 완전히 차단
📌 Security Service and Security Mechanism
| 보안 서비스 | 보안 메커니즘 |
| 데이터 기밀성 | 암호화 및 라우팅 제어 |
| 데이터 무결성 | 암호화, 디지털 서명, 데이터 무결성 |
| 인증 | 암호화, 디지털 서명, 인증 교환 |
| 부인봉쇄 | 디지털 서명, 데이터 무결성, 공증 |
| 접근 제어 | 접근 제어 메커니즘 |
여기서 부인 봉쇄란 내가 메시지를 보냈다는 사실을 부정할 수 없도록 만드는 것을 말한다.
2. 전통적인 대칭 키 암호화
📌 대칭 키 암호화 알고리즘의 개념
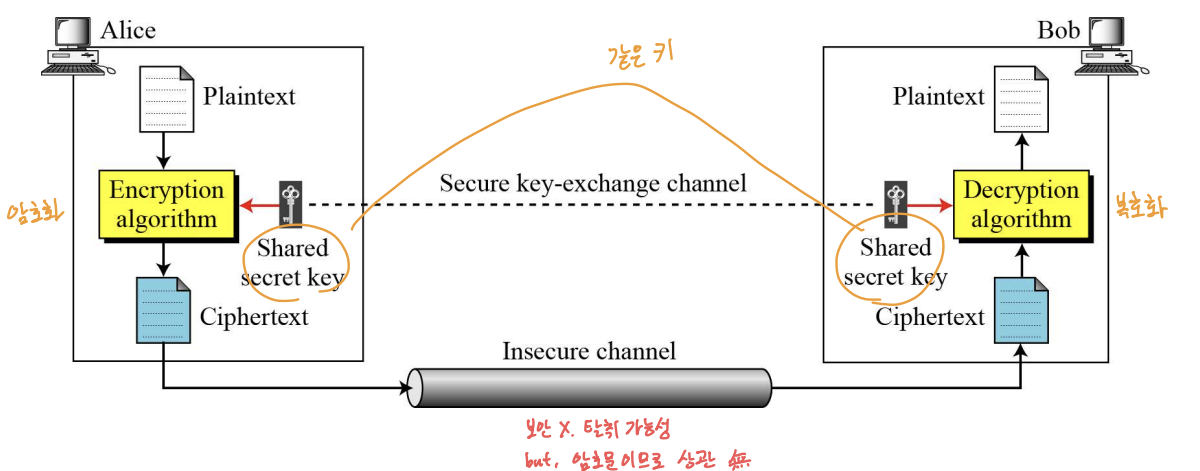
- 참여자: 송신자(Alice), 수신자(Bob), 공격자(Eve)
- 원 메시지: 평문(Plaintext), 채널을 통해 보내는 메시지: 암호문(Ciphertext)
- 암호 알고리즘(Encryption algorithm): 비밀 키를 이용해 평문 → 암호문 변환
- 복호 알고리즘(Decryption algorithm): 비밀 키를 이용해 암호문 → 평문 변환
- 암호와 복호에 사용되는 비밀 키(secret key)는 동일하다.
✒️ 평문, 암호문, 비밀키
- P가 평문, C는 암호문, K는 키라고 하자.
- 암호화: \( C = E_{k}(P) \)
- 복호화: \( P = D_{k}(C) \)
- 이 때, \( D_{k}(E_{k}(x)) = E_{k}(D_{k}(x)) = x \)를 가정 (역함수 관계)
- Alice: \( C = E_{k}(P) \), Bob: \( P_{1} = D_{k}(C) = D_{k}(E_{k}(P)) = P \)
- Kerckhoff의 원리
- 공격자 Eve는 항상 암호(E)/복호(D) 알고리즘은 알고 있다고 가정한다. (알고리즘은 숨길 수 없음. key를 숨겨야 한다.)
- 암호의 안전성은 키의 안전성에만 바탕을 둔다.
⚔️ 암호 해독

- 암호문 단독 공격: 가로 챈 암호문을 분석해서 대응되는 평문과 키를 파악
- 전수조사 공격(brute-force attack): 가로 챈 암호문에 모든 가능한 키를 사용하여 복호화하여 의미있는 평문을 생성
- 통계적인 공격(statistical attack): 평문 언어의 고유한 특징을 이용 (가장 빈번한 알파벳은 E이므로, 가장 빈번히 나타나는 문자를 일단 E를 대입해본다.)
- 패턴 공격: 암호문에 존재하는 패턴을 이용
- 알려진 평문 공격: 여러 개의 (평문, 암호문)의 쌍이 공격자에게 제공
- 선택 평문 공격: 공격자가 평문을 선택하고, 그에 따른 암호문이 제공
- 선택 암호문 공격: 공격자가 암호문을 선택하고, 그에 따른 평문이 제공
📌 대치 암호 (Substitution Ciphers)
- 하나의 기호를 다른 기호로 대체하는 방법
- 예를 들어, A는 D로, T는 Z로, 3은 7로 대체하는 방법
- 대치되는 문자가 1:1인지, 1:N인지에 따라 단일 문자 암호와 다중 문자 암호로 분류
✨ 단일 문자 암호 (Monoalphabetic ciphers)
1️⃣ 덧셈 암호 (Additive Cipher)


- 가장 간단한 암호로써, 이동 암호(Shift cipher), 혹은 시저 암호(Caesar cipher)라고 부른다.
- 평문, 암호문, 키는 모두 \(Z_{26}\)의 원소에 속한다. (%26을 해서 나오는 수의 집합)
🔐 암호화
k는 15라고 가정
| Plaintext | Encryption | Ciphertext |
| h → 07 | (07 + 15) mod 26 | 22 → W |
| e → 04 | (04 + 15) mod 26 | 19 → T |
| l → 11 | (11 + 15) mod 26 | 00 → A |
| l → 11 | (11 + 15) mod 26 | 00 → A |
| o → 14 | (14 + 15) mod 26 | 03 → D |
🔓 복호화
| Ciphertext | Decryption | Plaintext |
| W → 22 | (22 - 15) mod 26 | 07 → h |
| T → 19 | (19 - 15) mod 26 | 04 → e |
| A → 00 | (00 - 15) mod 26 | 11 → l |
| A → 00 | (00 - 15) mod 26 | 11 → l |
| D → 03 | (03 - 15) mod 26 | 14 → o |
이산 수학을 배운 적도 없고, 음수에 대한 모듈로 연산 자체가 오랜만이라 -15 mod 26의 값이 바로 안 떠올랐는데
-15/26 == -1이므로, -15 % 26은 11이 된다.
⚔️ 전수 조사를 이용한 암호문 해독
- 상황: Eve가 암호문 "UVACLYFZLJBYL"을 가로챘다. Eve는 키 값으로 1부터 7까지 대입했다.
- key가 7이면, 평문은 의미있는 값인 "not very secure"가 된다.
- 해봐야 26번이면 평문을 해독할 수 있으므로, 깨기 쉽다.
⚔️ 통계적인 공격을 이용한 암호문 해독(1)


덧셈 암호는 통계적 공격에 매우 취약하다.
예를 들어, Eve가 "XLILSYWIMWRSAJSVWEPIJSVJSYVQMPPMSRHSPPEVWMXMWASVX-LQSVILY-VVCFIJSVIXLIWIPPIVVIGIMZIWQSVISJJIVW"라는 암호문을 가로챘다고 가정하자.
문자들의 출현 빈도수를 기반으로 I=14, V=13, S=12이므로, I는 e와 대응될 수도 있음을 의미한다.
I를 e에 대응시키면 key는 4가 되므로, 암호문을 복호화하면 다음과 같은 평문을 얻을 수 있다.
"the house is now for sale for four million dollars it is worth more hurry before the seller receives more offers"
2️⃣ 곱셈 암호 (Multiplicative Cipher)

- K는 \(Z_{26}\)의 원소에서 역원이 존재하는 원소. 즉 \(Z_{26}*\)의 원소
- \(Z_{26}*\) = {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25} (최대 공약수 gcd(26, x) = 1)
- ex. (7 * 15) mod 26 = 1 (7의 곱셈에 대한 역원 ( \(7^{-1}\) ) = 15)
- 평문과 암호문은 \(Z_{26}\)의 원소
- 여기서 26 대신 23과 같은 소수를 선택하는 것이 더 좋은데, 다음과 같은 장점을 갖는다.
- 역원의 존재를 보장한다.
- 소수 p를 사용하면, 1부터 p-1까지의 모든 정수 a는 p에 대해 서로소이다.
- 즉, gcd(a, p)=1이며, 이 경우 모든 a에 대해 모듈로 p에서 역원이 존재하므로 key 선택이 쉽다.
- 역원 계산이 간단해진다.
- 소수 p에 대해, 모듈로 p에서 a의 역원은 유클리드 호제법으로 쉽게 도출할 수 있다.
- 특히, 페르마의 소정리를 이용하면 \(a^{p-1}\) ≡ 1 (mod p) 에서 \(a^{p-2}\) ≡ \(a^{-1}\) (mod p)가 성립하므로, 역원을 빠르게 구할 수 있다.
- 서로소의 특성을 활용할 수 있다.
- 소수 p를 사용하면, p와 p보다 작은 모든 수가 서로소 관계를 가지므로 모듈로 연산에서 문제가 발생하지 않는다.
- 암호 알고리즘의 안정성을 높이는 데 큰 도움을 준다.
- 역원의 존재를 보장한다.
✒️ 암호학에선 실수가 존재하지 않는다
일반적으로 4/3은 1.333333...이라는 실수가 되어야 겠지만, 암호학에선 4*\(3^{-1}\)로 표현한다.
\(3^{-1}\)은 3의 역수로서, 3 * x = 1로 표현 가능하다.
이 때, \(Z_{26}\)의 범위 내에서 3의 역수는 (3 * x) % 26 = 1, 즉 역원은 x = 9가 된다.
하지만 \(Z_{26}\)에 모두 역수가 존재하는가? 그렇지 않다.
(a * x) % 26 = 1이라는 식에, a를 0~25까지 대입하면서 역원(x)이 존재하는 a를 찾으면 {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25}뿐이다.
✒️ 역원이 존재해야 하는 이유
$$ K \times K^{-1} \equiv 1 \, mod \, N $$
(K는 N과 서로소인 숫자)
모듈로 N에서의 곱셈 역원은 반드시 위 조건을 만족해야 한다.
왜냐하면 K의 역원 \(K^{-1}\)이 존재해야만 암호화된 메시지를 복호화할 수 있기 때문이다.
예를 들어, N=23, K=2라고 가정했을 때, 2는 26과 서로소가 아니므로 mod 26에서 역원이 없다.
따라서 K = 2를 사용하면 복호화가 불가능하다.
반면, K=3을 사용하면 3 * 9 ≡ 27 ≡ 1 mod 26이므로, 역원은 9가 된다. 이 경우는 암호화/복호화 모두 가능하다.
🔐 암호화
key가 7인 곱셈 암호 사용하는 우
| Plaintext | Encryption | Ciphertext |
| h → 07 | (07 * 07) mod 26 | 23 → X |
| e → 04 | (04 * 07) mod 26 | 02 → C |
| l → 11 | (11 * 07) mod 26 | 25 → Z |
| l → 11 | (11 * 07) mod 26 | 25 → Z |
| o → 14 | (14 * 07) mod 26 | 20 → U |
🔓 복호화
암호문 "XCZZU"를 key = 7을 이용하여 복호화 하려면, D(\(C_{n}\) * 15) mod 26으로 수행하면 된다.
이 때, key가 7이므로 7의 역원 15를 대입해야 한다.
3️⃣ 아핀 암호 (Affine Cipher)

- 두 개의 키를 사용하고, 덧셈 암호와곱셈 암호를 결합한다.
- k1: 곱셈용 키. \(Z_{26}*\)의 원소
- k2: 덧셈용 키. \(Z_{26}\)의 원소
- 알고리즘
- 암호화: \(C = (P * k_{1} + k_{k2}) \, mod \, 26\)
- 복호화: \(P = ((C - k_{2}) * k_{1}^{-1}) \, mod \, 26\)
- 키 공간의 크기는 \(Z_{26} * Z_{26}*\) = 26 * 12 = 132
- 취약점
- 모든 경우의 수가 고작 132개이므로, brute force attack으로 해독 가능하다. (나중에 배울 오일러 피함수를 사용하면 아주 쉽게 풀 수 있다.)
- known plaintext attack으로 해독 가능하다.
- 암호문(AR) → 평문(IF)를 알고 있다면, A=0, F=5, I=8, R=17이다.
- f(8) = 8a + b = 0 mod 23, f(5) = 5a + b = 17 mod 26를 연립 방정식으로 풀이하면, a=3, b=2
- \(k_{1}\) = 3, \(k_{2}\) = 2이므로, \(f^{-1}(x) = 3^{-1}(x-2) = 9(x-2) \, mod \, 26\)으로 전체 해독 가능.
🔐 암호화
키 쌍이 (7, 2)인 경우
| Plaintext | Encryption | Ciphertext |
| h → 07 | (07 * 7 + 2) mod 26 | 25 → Z |
| e → 04 | (04 * 7 + 2) mod 26 | 04 → E |
| l → 11 | (11 * 7 + 2) mod 26 | 01 → B |
| l → 11 | (11 * 7 + 2) mod 26 | 01 → B |
| o → 14 | (14 * 7 + 2) mod 26 | 22 → W |
🔓 복호화
| Plaintext | Decryption | Ciphertext |
| Z → 25 | ((25 - 2) * \(7^{-1}\)) mod 26 | 07 → h |
| E → 04 | ((04 - 2) * \(7^{-1}\)) mod 26 | 04 → e |
| B → 01 | ((01 - 2) * \(7^{-1}\)) mod 26 | 11 → l |
| B → 01 | ((01 - 2) * \(7^{-1}\)) mod 26 | 11 → l |
| W → 22 | ((22 - 2) * \(7^{-1}\)) mod 26 | 14 → o |
✨ 다중 문자 암호 (Polyalphabetic ciphers)
단일 문자 암호는 통계적 공격에 매우 취약하다는 단점이 있다.
이 문제를 해결하려면 통계적 빈도 차이를 없애야 하는데, 하나의 문자가 N개의 문자에 대응하도록 만들면 된다.
플레이페어 암호(Playfaire Cipher)와 Hill 암호는 수업 시간에 다루지 않았는데, 궁금해서 추가로 찾아본 내용이라 틀렸을 수 있습니다.
1️⃣ 자동 키 암호 (Autokey Cipher)

- key는 부분 키들로 구성된 수열로써, 첫 번째 키는 미리 정의하고, 나머지 키는 평문의 문자들을 차례로 사용한다.
- \(P = P_{1}P_{2}P_{3}\dots\), \(C = C_{1}C_{2}C_{3}\dots\), \(k = (k_{1}, P_{1}, P_{2}, \dots\))
- Encryption: \(C_{i} = (P_{i} + k_{i}) \, mod \, 26\)
- Decryption: \( P_{i} = (C_{i} - k_{i}) \, mod \, 26 \)
- pros
- 키 스트림이 평문에 따라 변하므로 반복성이 낮으므로, 빈도 분석 공격에 비교적 강하다.
- 초기 키만 알고 있으면 나머지 키는 평문으로 생성하므로, 키 관리가 비교적 쉽다.
- cons
- 알려진 평문 공격(Known-plaintext attack)에 취약하다.
2️⃣ Vigenere 암호

- key는 m개의 덧셈 암호를 사용한다.
- \(P = P_{1}P_{2}P_{3}\dots\), \(C = C_{1}C_{2}C_{3}\dots\), \(K = [(k_{1}, k_{2}, \dots, k_{m}), (k_{1}, k_{2}, \dots, k_{m}), \dots]\)
- Encryption: \(C_{i} = P_{i} + k_{i}\)
- Decryption: \(P_{i} = C_{i} - k_{i}\)
- 카지스키, 프리드만 암호 공격 방법으로 해독할 수 있다. (문장이 길어지면 반복되는 패턴이 생겨, 키의 길이를 추측할 수 있기 때문)
3️⃣ 플레이페어 암호 (Playfair Cipher)
[보안] 플레이페어 암호화란?
플레이페어 암호 (Playfair cipher)란? 플레이페어 암호화는 영국의 물리학자 휘트스톤과 영국의 수학자 플레이페어가 함께 만든 함호화 방식입니다. 휘트스톤이 죽은다음 발표를 하게되어 이 암호
sizzf.tistory.com
- 평문에서 두 문자를 동시에 암호화한다.
- 임의의 문자열 key로 만든 5*5 크기의 key 테이블을 사용한다..
- key의 중복 문자를 제거하여 낮은 row, 낮은 col 순으로 문자를 채운다.
- 남은 칸은 아직 사용하지 않은 알파벳을 중복없이 순서대로 채운다. (I/J 혹은 Q/Z를 같은 자리에 넣어야 한다.)
- 암호화 규칙
- 문장을 2글자씩 나눈다. (한 쌍의 문자가 같거나, 마지막에 하나 남은 문자가 있다면 두 번째 문자는 X가 온다.)
- 암호화하는 두 문자가 서로 다른 행과 열에 존재하는 경우, 각 문자의 열을 기준으로 페어의 문자가 같은 행이 되는 위치의 알파벳으로 치환한다.
- 두 문자가 같은 열에 있는 경우, 한 칸 아래로 내려간다. (더이상 이동갈 곳이 없다면 제일 위로)
- 두 문자가 같은 행에 있는 경우, 한 칸 우측으로 간다. (더이상 이동할 곳이 없다면 제일 좌측으로)
- 복호화 규칙
- 문장을 2글자씩 나눈다. (위와 동일한 규칙)
- 규칙1 동일
- 규칙 2,3은 반대 방향으로 움직인다.
5*5 행렬이므로 가능한 행렬 개수가 25!
그러나 암호화 규칙을 잘 생각해보면 행, 열의 순서가 바뀌더라도 같은 키가 된다.
1행에 있는 {F, A, I, R, E}와 3행의 {T, P, U, X, J}의 순서를 바꿔도 암호화 규칙의 결과가 동일해지므로, 실제 탐색해야 하는 수는 \(25! / 25 = 6 * 10^{23} \)개.
하지만 알파벳 문자 빈도나 문자 쌍의 빈도를 이용하여, Ciphertext-only attack에 취약하다(고 하는데 이유를 모르겠다...)
4️⃣ Hill 암호
Hill cipher - Wikipedia
From Wikipedia, the free encyclopedia Substitution cipher based on linear algebra Hill's cipher machine, from figure 4 of the patent In classical cryptography, the Hill cipher is a polygraphic substitution cipher based on linear algebra. Invented by Lester
en.wikipedia.org
- n*n의 키 행렬(key matrix)를 사용한다.
- Encryption: \(C = P \cdot K \, mod \, 26\) (단, \(K = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \))
- Decryption: \(P = C \cdot K^{-1} \, mod \, 26 \) (단, \(K^{-1} = \frac{1}{ab-bc} \begin{bmatrix} b & -b \\ -c & a \\ \end{bmatrix}\))
- 여기서 \((ad-bc)^{-1} \, mod \, 26\) → \(gcd(ad-bc, 26) = 1\)
- Brute Force 공격은 \(26^{N^{2}}\)개에서 역행렬이 없는 행렬을 제외한 경우의 수지만, 여전히 너무 많아서 사실상 불가
- 암호문만으로는 key나 Plaintext를 구하기 어려우므로, Ciphertext-only 공격에는 안전하다.
- Known plaintext attck으로 해독 가능하다.
- \(C = \bigl (\begin{smallmatrix} 15 & 2 \\ 16 & 5 \end{smallmatrix}\bigr) \)이고, \(P = \bigl (\begin{smallmatrix} 5 & 8 \\ 17 & 3 \end{smallmatrix}\bigr) \)인 경우, \(P \cdot K = C\)이므로 \(K = C \cdot P^{-1}\)
- \(P^{-1} = \frac{1}{ab-bc} \begin{bmatrix} b & -b \\ -c & a \\ \end{bmatrix} = \frac{1}{15-136} \bigl(\begin{smallmatrix} 3 & -8 \\ -17 & 5 \end{smallmatrix}\bigr) \)
- \(-151^{-1} \, mod \, 26 = 9^{-1}\), 역원은 3
- 따라서, \( 3 \bigl(\begin{smallmatrix} 3 & -8 \\ -17 & 5 \end{smallmatrix}\bigr) \, mod \, 26 = \bigl(\begin{smallmatrix} 9 & 2 \\ 1 & 15 \end{smallmatrix}\bigr) \)
- \(K = C \cdot P^{-1} = \bigl(\begin{smallmatrix} 15 & 2 \\ 16 & 5 \end{smallmatrix}\bigr) \cdot \bigl(\begin{smallmatrix} 3 & -8 \\ -17 & 5 \end{smallmatrix}\bigr) \, mod \, 26 = \bigl(\begin{smallmatrix} 7 & 8 \\ 19 & 3 \end{smallmatrix}\bigr) \)
다른 방식으로도 조건이 주어지는 경우가 있는데, 패스
📌 치환(전치) 암호 (Transposition Ciphers)
- 한 기호를 다른 기호로 대체시키지 않고, 대신 그 기호의 위치를 바꾸는 방법 (기호 재정렬)
1️⃣ 키가 없는 전치 암호 (Keyless Transposition Ciphers)

- 평문을 지그재그 패턴으로 배열
- 암호문은 행 순서의 패턴으로 읽혀져 생성된다.


- 평문의 각 문자를 암호문으로 바꾸는 순열로 표시한다.
2️⃣ 키가 있는 전치 암호 (Keyed Transposition Ciphers)

- 사전에 정의된 크기(Block)로 평문을 나누고 각각의 Block에 독립적으로 키를 사용하여 문자를 치환
3️⃣ 두 가지 접근법의 결합

- 3단계의 암호화/복호화
- 표에 행 순서로 기록 → 열을 재배열 → 표를 열 순서로 읽는다.
4️⃣ 이중 전치 암호 (Double Transposition Ciphers)

- (3)의 방법을 한 번 더 반복한다.
이딴 게 암호화...? 싶겠지만, 내 기억이 맞으면 sha 알고리즘도 특정 연산을 엄청나게 많이 반복해서 암호화하는 것으로 알고있다.
3. AES (Advanced Encryption Standart)
📌 Introduction

- 2001년 미국 국립기술표준원(NIST)에서 공표한 대칭 키 암호 알고리즘
- 128-bit 평문을 128-bit 암호문으로 출력
- 128,192, 256 bit key를 사용하고, 키 크기에 따라 각각 10, 12, 14 round를 갖는 3가지 버전이 존재
🟡 AES 데이터 단위

- 1byte = 8bit
- 1word = 4byte
- 1block = 4word
- state는 Block의 암호화 중간 단계
🟡 State와 Block 변환

- \(block_{i}\) → \(S_{i \, mod \, 4, \, i/4}\)
- \(s_{i,j}\) → \(block_{i + 4j}\)
🟡 AES 기본 구조

처음보면 이게 뭐지...? 하고 다급하게 뒤로가기를 연타할 수 있으나, 공장 마냥 특정 연산을 반복적으로 수행하고 있다고 보면 된다.
밑에서 하나씩 자세하게 다루므로 간단히 흐름만 정리.
- 키 확장 (Key Expansion)
- 암호화 키를 여러 라운드 키로 확장한다.
- \(W_{0}, W_{1}, W_{2}, W_{3}\)으로 시작하여 \(W_{43}\)까지 확장
- 초기 라운드
- 평문 블록에 첫 번째 라운드 키를 더한다. (AddRoundKey)
- \(S = B \bigoplus K_{0} \)
- 메인 라운드 (4단계로 구성된 라운드가 총 9번 수행)
- SubBytes: 바이트 단위로 치환한다.
- ShiftRows: 행 단위로 바이트를 이동한다.
- MixColumns: 열 단위로 바이트를 혼합한다.
- AddRoundKey: 라운드 키를 더한다.
- 최종 라운드 (3단계로 구성)
- SubBytes
- ShiftRows
- AddRoundKey
- 복호화
- 복호화는 암호화의 역순으로 수행하여, 각 라운드의 역 연산으로 평문을 복월한다.
📌 AES에서 사용하는 변환 함수
1️⃣ 대치(Substitution) - SubBytes (InvSubBytes)

- 16개의 독립된 byte 단위의 변환을 수행한다.
- 각 byte를 4bit씩 2개의 16진수로 계산하고, 왼쪽 4bit를 row로 오른쪽 4bit를 col으로 S-Box의 테이블을 읽는다.
이건 이해하는 내용이 아니다.
아래와 같은 변환 표를 보고 읽으면 된다.


계속 보면 눈이 급속도로 피로해지므로, 2개 정도만 해보면 얼추 뭔지 이해할 수 있다.
2️⃣ 치환(Permutation) - ShiftRows (InvShiftRows)


- ShiftRows: 암호화 과정에서 사용하고, 바이트 단위의 left-shift 수행
- 각 row마다 이동 규칙이 다른 것이 특징. 0번 row는 이동이 없고, 1번 row는 1byte, 2번 row는 2byte, 3번 row는 3byte 움직인다.
- InvShiftRows: 복호화 과정에서 사용하고, 바이트 단위의 right-shift 수행 (위와 동일)
3️⃣ 뒤섞음(Mixing) - MixColumns (InvMixColumns)

- 행렬 곱을 이용하여 각 state의 열(column)을 새로운 열로 변환
- Byte들의 곱셈: GF(2^8)에서 \(x^{8} + x^{4} + x^{3} + x + 1\)의 나머지 (기약 다항식; irreducible polynomial)
- Byte들의 덧셈: 8-bit 단위의 XOR 연산
- Constent Vector(상수 벡터; C)
- 암호화 시 C벡터를 사용했다면, 복호화 시에는 \(C^{-1}\) 벡터를 사용해야 한다.
🥲 기약 다항식은 또 뭔데..
행렬 곱셈을 하다보면 값이 너무 커질 수 있으므로 모듈로 연산을 지속적으로 해주어야 한다.
대충 (3 * 17) % 26처럼 해주고 싶다는 건데, 문제는 AES에서는 데이터가 8bit 단위이므로 2^8 범위의 수가 곱해질 수 있다.
문제는 256이 소수가 아니므로 역원이 존재하지 않을 수도 있는데, 이 때문에 256에서 가장 가까운 소수가 253이라고 치면 8bit를 모두 활용하지 못하는 불상사가 생긴다. (곱셈 암호화에서 역원의 필요성에 대해선 이미 언급했다.)
그럼 이 문제를 어떻게 해결하면 좋을까?
바로, 8-bit를 모두 활용할 수 있는 다항식을 만들면 된다.
우선 다항식은 나눌 수 있는 다항식이 자기 자신 하나만일 경우 기약(irreducible)이라고 한다.
AES 알고리즘에선 \(m(x) = x^{8} + x^{4} + x^{3} + x + 1\)을 기약 다항식으로 사용하며, 16진수 표현으로 {01}{1b}이 되는 것이다.
🟡 0x63 → 0x62가 계산되는 MixColumns 예시

- \(02 \cdot 63 \, \bigoplus \, 03 \cdot F2 \, \bigoplus \, 01 \cdot 7D \, \bigoplus \, 01 \cdot D4 \) (⊕는 XOR 연산)
- \begin{align} 02\cdot 63 &= (000 \, 0010)\cdot (0110 \, 0011)\\ &= (x * (x^{6} + x^{5} + x + 1)) \, mod \, (x^{8} + x^{4} + x^{3} + x + 1)\\ &= x^{7}+x^{6}+x^{2}+x = 1100 \, 0110 \end{align}
- \begin{align} 03\cdot F2 &= ((x+1) * (x^{7}+x^{6}+x^{5}+x^{4}+x)) mod (x^{8}+x^{4}+x^{3}+x+1)\\ &= (x^{8}+x^{7}+x^{6}+x^{5}+x^{2}+x^{7}+x^{6}+x^{5}+x^{4}+x) \, mod \, (\dots)\\ &= (x^{8}+x^{4}+x^{2}+x) \, mod \, (x^{8} + x^{4} + x^{3} +x + 1)\\ &= x^{3} + x^{2} + 1 = 0000 \, 1101 \end{align}
- \(01\cdot 7D = (0000 \, 0001)\cdot(0111 \, 1101) = 0111 \, 1101\)
- \(01\cdot D4 = (0000 \, 0001)\cdot(1101 \, 1000) = 1101 \, 0100\)
- 1100 0110 ⊕ 0000 1101 ⊕ 0111 1101 ⊕ 1101 0100 = 0110 0010 = 0x62
4️⃣ 키 덧셈(Key Adding) - AddRoundKey

AddRoundKey(S)
{
for (c = 0 to 3)
\(s_{c}\) ← \(s_{c}\) ⊕ \(W_{4round + c}\)
}
- 각 state의 열 행렬에 라운드 키(round key)를 더한다.
- 라운드 키는 대칭 키를 확장하여 생성
📌 AES 키 확장 과정

KeyExpansion([key0 to key15], [w0 to w43]) { // AES-128에서 키: 128bit, 11 round
for (i=0 to 3)
wi = key4i + key4i_plus1 + key4i_plus2 + key4i_plus3 // 암호 키로 처음 round key 생성
for (i=4 to 43) {
if (i mod 4 != 0) // 각 round의 2~4번 째 round key
wi = wi_minus1 + wi_minus4 // 2개의 이전 round key로 다음 key 생성
else { // 각 round의 첫 번째 round key
t = SubWord(RotWord(wi_minus1)) XOR RCon_i_divide_4 // t는 temporary word
wi = t + wi_minus4 // 이전 라운드의 첫 번쨰 key와 t를 XOR
}
}
}- 하나의 암호키로부터 \(N_{r} + 1\)개의 128-bit round 키를 생성 (\(N_{r}\): round의 수)
- 암호 키의 크기: 128-bit(AES-128), 192-bit(AES-192), 256-bit(AES-256)
아놔, 여기서부터 이해하는데 한참 걸리네.
여기서부턴 교수님도 이해하길 바라지 않으셨는지, 휙휙 지나가버려서 한참을 더 봤다.
🤔 t는 어떻게 계산하는데?
- t ← SubWord (RotWord(\(w_{i-1}\))) ⊕ \(RCon_{i/4}\)
- RotWord: ShiftRows처럼 한 바이트씩 shift-left
- SubWord: SubBytes의 S-Box를 이용하여 4-byte 대치
- RCon(Round Constant): 각 round에서 사용하는 상수값
- \(w_{03}\)이 13AA5487일 때, round1의 t를 계산하는 과정
- RotWord(13AA5487) = AA548713
- SubWord(AA548713) = AC20177D
- t = AC20177D ⊕ RCon1 = AC20177D ⊕ 01000000_16 = AD20177D → t4로 사용
🟡 AES-128에서 round key를 생성하는 2가지 예시


- 왼쪽은 단일 암호키를 사용하는 경우고, 오른쪽은 오직 한 비트만 다른 값을 갖는 두 암호키로 라운드 키를 생성하는 방식이다.
- 오른쪽의 장점은 1bit 차이밖에 나지 않음에도 불구하고, Round가 지날수록 결과가 완전히 바뀌어 원본 값을 유추하기 매우 어렵게 만든다.
💡 AES 키 확장 과정 특징
- 암호키 일부나 라운드 키 일부 값으로 나머지 키 값을 유추할 수 없다.
- 오직 한 비트만 다른 두 개의 암호 키도 적은 수의 라운드만에 서로 다른 라운드 키를 생성한다.
- 상수 RCons는 라운드 키들 사이의 대칭성을 제거해준다.
- AES에서는 심각한 취약 키가 존재하지 않는다.
- 키 확장 과정은 거의 대부분 환경에서 쉽게 구현 가능하다.
- 테이블을 저장하지 않고도 모든 계산을 GF(2^8) 또는 GF(2) 체를 사용하여 표현 가능하다.
📌 AES 분석
1️⃣ 보안
- Brute-Force Attack의 경우, 경우의 수가 2^128 (AES-128)이므로 전탐색으로는 공격 어려움
- 수많은 테스트들이 AES 암호문 통계적 분석 공격 실패 (통계, 패턴 분석 방어)
2️⃣ 구현 용이성
- AES는 소프트웨어, 하드웨어, 펌웨어로 구현 가능
- Table lookup 또는 대수적 구조를 사용하는 루틴을 사용하여 구현 가능
3️⃣ 단순성과 비용
- AES에 사용하는 알고리즘은 매우 단순
- 값싼 프로세서와 최소 메모리만으로도 쉽게 구현 가능