[C++] 10265 - MT (플래티넘4)

1. 문제 설명

 

10265번: MT

이제 MT 갈 때 됐으니, MT 문제를 풀어보라던 스터디원의 권유로 보게 된 문제.

오랜만에 코테 문제 푼다고 새벽 3시까지 못잤다.

장장 10시간 정도를 풀었던 것 같다. 🤮

물론, 그 사이에 프로젝트 때문에 개발을 멀티로 수행했다는 것도 문제였던 거 같기도 한데, 문제만 봤어도 금방은 못 풀었을 것 같다.

 

---

2. 아이디어

 

보자마자 위상정렬(Topological Sort) 문제겠거니 했다.

"내가 가려면 누군가(선행조건)가 가야 한다."식의 문제이므로, '나'의 진입 차수를 1 증가시키고 선행 조건이 만족되는지를 판단하면 된다.

문제는 당장은 위상정렬을 적용할 수가 없다.

 

📌 반례 : 순환 간선

입력1

모두가 자기 자신을 지목한 경우, 다른 사람에게 의존하지 않는다.

이럴 때, 버스에 여유 공간만 있다면 최대 4명을 태울 수 있게 된다.

 

예시

임의로 만들어 본 테스트 케이스도 쉽게 풀 수 있다.

선행 조건이 만족되어야 내가 가는 거지, 꼭 친구가 탄다고 내가 타야하는 건 또 아니므로

탑승 인원을 1~4까지 다양한 결과를 도출할 수 있다.

 

입력2

문제는 이 경우다.

{4 5 6 7}은 서로가 서로를 선행조건으로 두는 사이클이 형성되므로, 전부 다 타거나, 한 명도 안 타거나 두 가지 선택지 밖에 없다.

{4 5 6 7}이 상호 의존적 관계를 보이므로, 당장은 일반적인 위상정렬 기법인 Back Edge(트리에서 자손에 위치한 노드가 조상 노드와 이어지는 Edge)를 끊어내는 방식으로 문제를 해결할 수가 없게 된다.

 

따라서 문제를 위상 정렬로 풀기 위해 사이클을 묶어줄 필요가 있었고,

DAG로 만들기 이전에 그래프를 SCC(Strongly Connected Component)단위로 묶어야만 했다.

 

✒️ 문제 입력

for (int i = 0, u; i < n; i++) {
    cin >> u;
    adj[u-1].push_back(i);
}

참고로 문제 입력을 받는 adj는 "'나'를 선행 조건으로 갖는 노드 리스트"를 표현한다.

 

📌 SCC 만들기

[Python] 2150 - Strongly Connected Component (플래티넘5)

(옛날 옛적에 풀었었던 SCC 문제)

 

입력2

• 1~10번 노드가 엮인 그래프는 최소 4명부터 버스에 태울 수 있다.
• 11~12번 노드가 엮인 그래프는 1~2명을 버스에 태울 수 있다.

이 문제의 재밌는 점은 하나의 트리에서 사이클은 언제나 단 하나밖에 나올 수 없다는 점이다.

• 모든 노드는 단 하나의 선행 조건만을 가진다.
• 따라서 사이클에 해당하는 노드 외에 다른 노드가 사이클을 형성하면 다른 트리가 형성될 수밖에 없다.

 

🟡 타잔 알고리즘

SCC 알고리즘

 

강한 연결 요소 (SCC) - 타잔 알고리즘

SCC를 만들기만 하면 되므로, 예전에 내가 사용한 방법인 코사라주 알고리즘(Kosaraju's Algorithm)을 사용해도 무방하다.

둘 다 O(V + E)의 시간복잡도가 걸리는 아주 야무진 녀석들이다. (V가 정점 개수, E가 간선 개수)

 

다만 코사라주 알고리즘은 코드가 너무 방대해지는 게 개인적으로 별로 마음에 안 들어서, 이 참에 타잔 알고리즘을 찾아봤다.

이 아름다운 알고리즘의 실행 동작은 다음과 같다.

 

• 1번 정점에서 dfs를 시작한다.
• 방문할 때마다 임의의 stack에 방문한 정점을 저장한다.

 

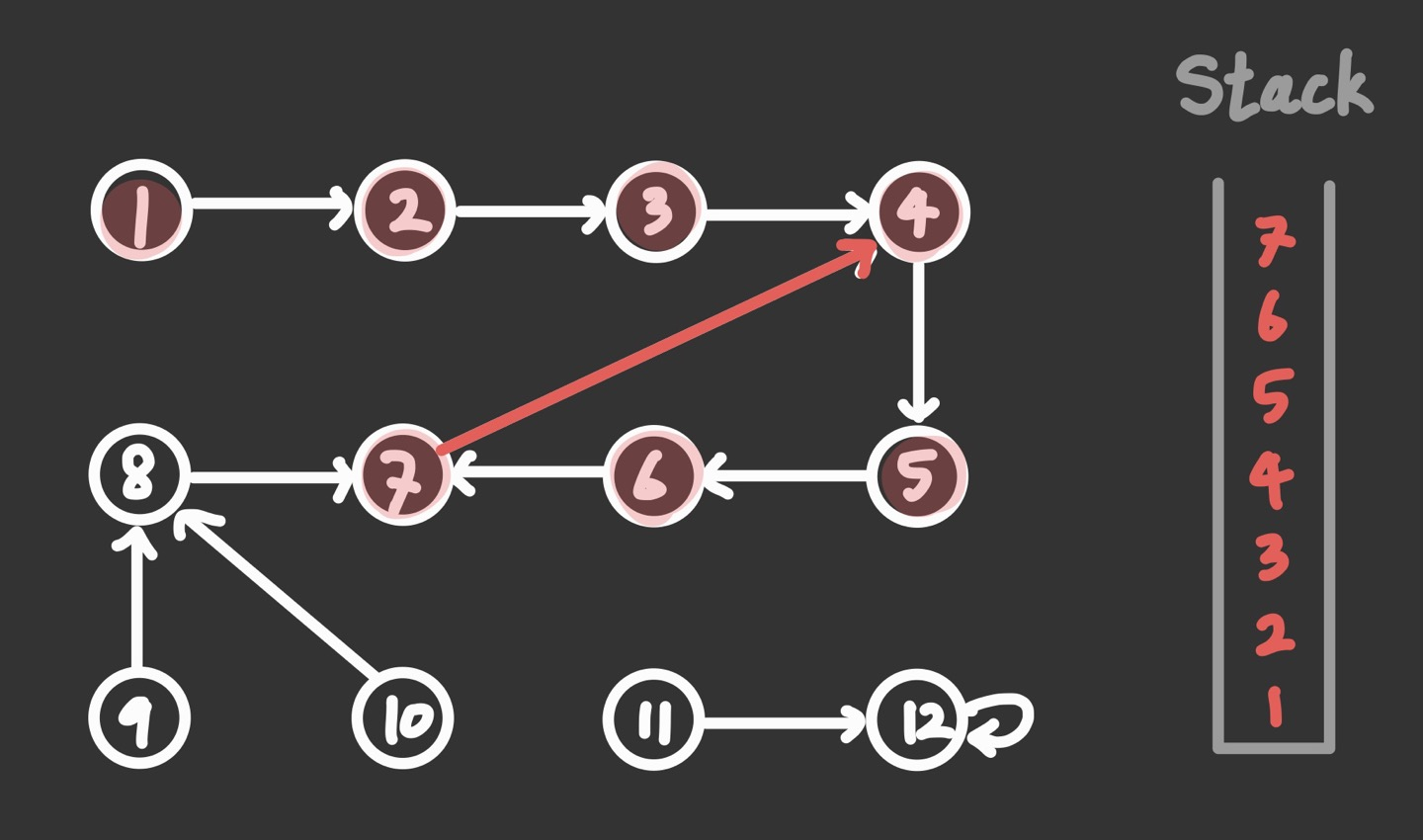
• 이미 방문한 정점을 재진입하는 경우 (7 → 4)
• stack에서 하나씩 pop하면서 자기 자신 4가 나올 때까지 SCC로 라벨링한다.

 

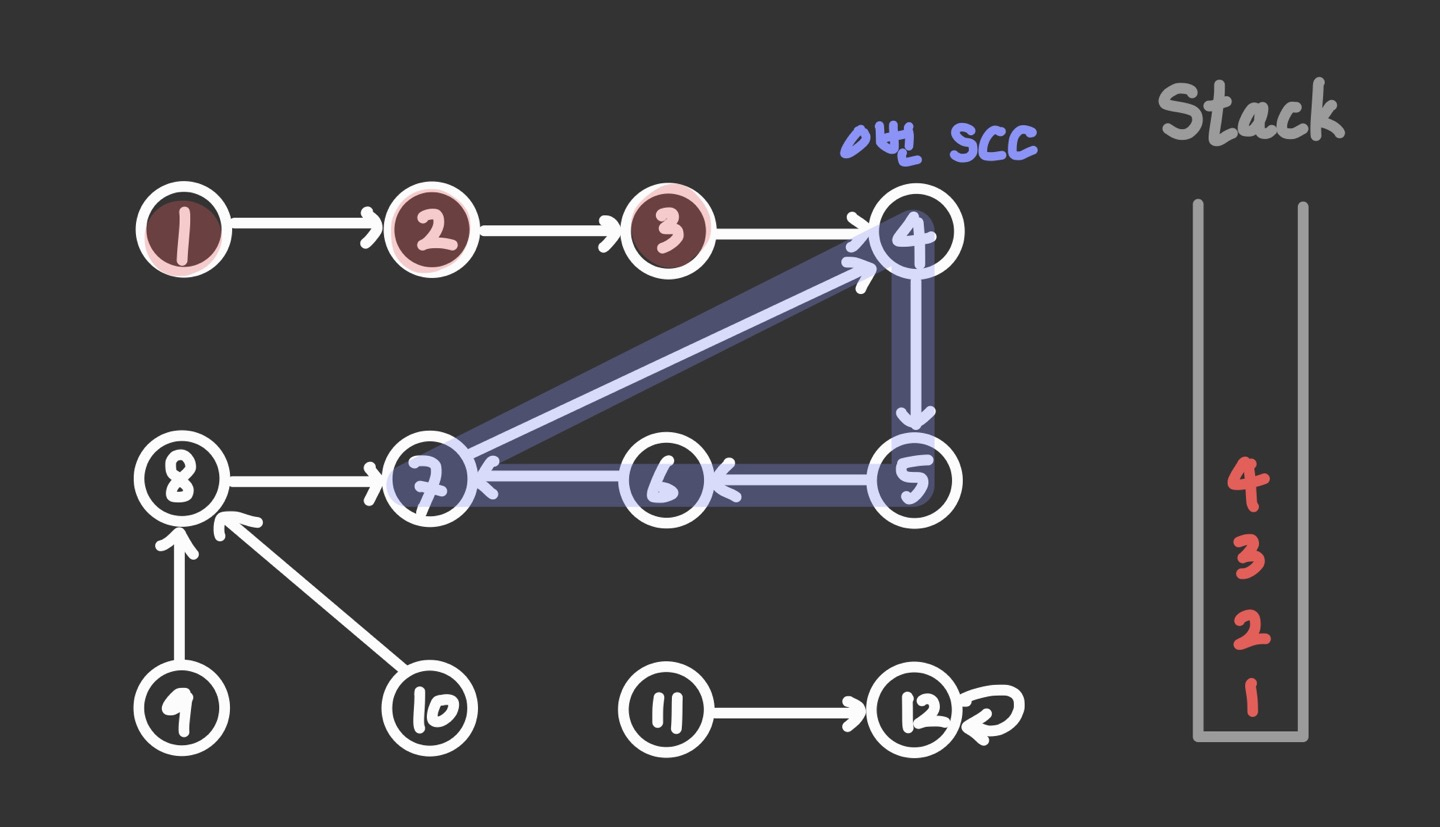
• 이 짓을 다른 방문하지 않은 정점들에 대해서도 반복문을 돌려주면 완성이다.

 

코드는 두 번째 블로그의 양식을 거의 그대로 적용해서 구현했다.

int n, k;
int visited[MAX], sccLabel[MAX], sccSize[MAX];
int idx=0, sccCnt=0;
vector<int> adj[MAX];
stack<int> s;

void tarjan() {
    for (int i = 0; i < n; i++)
        if (!visited[i]) makeSSC(i);
}

int makeSSC(int curr) {
    int dfsn = visited[curr] = ++idx; // DFS 탐색 순서를 저장한다.
    s.push(curr);

    for (int nxt : adj[curr]) {
        if (!visited[nxt]) dfsn = min(dfsn, makeSSC(nxt)); // 방문하지 않은 노드라면 DFS를 계속 진행한다.
        else if (sccLabel[nxt] == -1) dfsn = min(dfsn, visited[nxt]); // 방문은 했지만, 아직 SCC로 묶이지 않은 노드라면 
    }

    if (dfsn == visited[curr]) { // DFS 탐색 순서가 현재 노드의 순서와 같다면 SCC를 생성한다.
        while (true) {  
            int node = s.top(); s.pop();
            sccLabel[node] = sccCnt; // SCC 번호를 저장한다.
            sccSize[sccCnt]++; // SCC의 Component 크기를 저장한다.
            if (node == curr) break; // 현재 노드가 SCC의 루트라면 SCC 생성을 마친다.
        }
        sccCnt++;
    }

    return dfsn;
}

 

📌 비순환 그래프(DAG, Directed Acyclic Graph)로 만들기 

• 있어 보이려고 어려운 용어 끌고 와본 거고, 그냥 순환 구간이 없는 그래프를 말한다.
• 즉, 위상 정렬된 형태로 만듦으로써 문제 조건을 변경했다.
• 위에서 SCC끼리 묶어줬으므로 사이클이 존재하던 노드를 root로 하는 역방향 트리를 만들 것이다.

 

int visited[MAX], sccLabel[MAX], sccSize[MAX];
int compNum = 0;
int compIndex[MAX], minCompSize[MAX], maxCompSize[MAX];
vector<int> adj[MAX];

void makeDAG() {
    vector<int> graph[MAX];
    int indegree[MAX] = {0};

    for (int i=0; i<n; i++) {
        int nodeNum = sccLabel[i];
        for (int adjNode : adj[i]) {
            int nextNodeNum = sccLabel[adjNode];
            if (nodeNum == nextNodeNum) continue;
            graph[nodeNum].push_back(nextNodeNum); // nodeNum -> nextNodeNum
            indegree[nextNodeNum]++; // nextNodeNum의 indegree 증가
        }  
    }

    queue<int> q;
    for (int i=0; i<sccCnt; i++) if (indegree[i] == 0) {
        q.push(i);
        compIdx[i] = ++compNum; // indegree가 0인 노드는 SCC의 최상위 노드이므로, 최소 인원은 1명이다.
        minCompSize[compNum] = maxCompSize[compNum] = sccSize[i]; // SCC의 크기를 저장한다.
    }

    while (!q.empty()) {
        int curr = q.front(); q.pop();
        for (int nxt : graph[curr]) {
            compIdx[nxt] = compIdx[curr]; // nextNodeNum의 최소 인원은 currNodeNum의 최소 인원 + 1이다.
            maxCompSize[compIdx[nxt]] += sccSize[nxt]; // nextNodeNum의 최대 인원은 currNodeNum의 최대 인원 + nextNodeNum의 크기이다.

            if (--indegree[nxt] == 0) q.push(nxt);
        }
    }
}

1. 첫 번째 for문에서 SCC를 토대로 역방향 그래프를 만든다.
   • 사이클이 root node로 바뀐다.
   • 다음 component로 이동할 때마다 진입 차수가 1씩 증가한다.
2. 두 번째 for문에서 진입 차수가 0인 Root Component에 대해 3가지 정보를 초기화한다.
   • compIndex : 컴포넌트 넘버 (네이밍 일관성을 위해 compLabel이 더 적합했을 것 같다.)
   • minCompSize : 해당 컴포넌트에서 버스에 태울 수 있는 최소 인원 수
   • maxCompSize : 해당 컴포넌트에서 버스에 태울 수 있는 최대 인원 수
3. 마지막 while문에서는 하위 노드를 차례로 순회하면서 해당 component의 maxCompSize를 갱신한다.
   • 다음 노드의 진입차수를 1씩 내리면 queue에 넣을 수 있다.

 

📌 배낭 문제(Knapsack Problem)

12865번: 평범한 배낭

DP에서 매우 유명한 문제 중 하나.

어떤 배낭 안에 넣을 수 있는 최대 무게가 K일 때, 배낭에 넣을 수 있는 N개의 물건이 각기 다른 가치(V)와 무게(W)를 가질 때, 배낭이 최대한 가치가 높은 물건들을 담을 수 있는 조합을 탐색한다.

 

해당 아이디어에 알고리즘 코테 책에서 공부한 dp 레시피를 그대로 적용해서 로직을 구현했다.

 

🟡 Knapsack Problem 적용

• cache[now][value] : 현재 컴포넌트(now)에서 빈 자리(value)에 태울 수 있는 최대 인원 
• 그냥 넣다 뺐다 해보면 되는 정도의 로직이라 쉽게 구현할 수 있다.

 

int compNum = 0;
int compIdx[MAX], minCompSize[MAX], maxCompSize[MAX];
int cache[MAX][MAX];

int knapsack(int now, int value) {
    if (now > compNum) return 0;

    int& ret = cache[now][value];
    if (ret != -1) return ret;

    ret = knapsack(now+1, value); // 상위 컴포넌트에서 한 명도 안 태우는 경우
    if (value >= minCompSize[now]) {
        for (int i=minCompSize[now]; i<=maxCompSize[now]; i++) {
            if (i > value) break; // 더 이상 여석이 없으면 탐색 중단
            ret = max(ret, knapsack(now+1, value-i) + i); // 현재 컴포넌트에서 태우고, 다음 컴포넌트 확인
        }
    }

    return ret;
}

 

---

3. 코드

 

#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <cstring>

#define MAX 1001
#define endl '\n'

using namespace std;

int n, k;
int visited[MAX], sccLabel[MAX], sccSize[MAX];
int idx=0, sccCnt=0;
int compNum = 0;
int compIndex[MAX], minCompSize[MAX], maxCompSize[MAX];
vector<int> adj[MAX];
int cache[MAX][MAX];
stack<int> s;

void init();
void tarjan();
int makeSSC(int curr);
void makeDAG();
int knapsack(int now, int value);
bool finished[MAX];

int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    init();
    tarjan();
    makeDAG();
    cout << knapsack(1, k) << endl;
}

void init() {
    cin >> n >> k;

    for (int i = 0, u; i < n; i++) {
        cin >> u;
        adj[u-1].push_back(i);
    }

    for (int i=0; i<MAX; i++) memset(cache[i], -1, sizeof(cache[i]));
    memset(sccLabel, -1, sizeof(sccLabel));
    fill(&cache[0][0], &cache[MAX-1][MAX], -1);
}

void tarjan() {
    for (int i = 0; i < n; i++)
        if (!visited[i]) makeSSC(i);
}

int makeSSC(int curr) {
    int dfsn = visited[curr] = ++idx; // DFS 탐색 순서를 저장한다.
    s.push(curr);

    for (int nxt : adj[curr]) {
        if (!visited[nxt]) dfsn = min(dfsn, makeSSC(nxt)); // 방문하지 않은 노드라면 DFS를 계속 진행한다.
        else if (sccLabel[nxt] == -1) dfsn = min(dfsn, visited[nxt]); // 방문은 했지만, 아직 SCC로 묶이지 않은 노드라면 
    }

    if (dfsn == visited[curr]) { // DFS 탐색 순서가 현재 노드의 순서와 같다면 SCC를 생성한다.
        while (true) {  
            int node = s.top(); s.pop();
            sccLabel[node] = sccCnt; // SCC 번호를 저장한다.
            sccSize[sccCnt]++; // SCC의 Component 크기를 저장한다.
            if (node == curr) break; // 현재 노드가 SCC의 루트라면 SCC 생성을 마친다.
        }
        sccCnt++;
    }

    return dfsn;
}

void makeDAG() {
    vector<int> graph[MAX];
    int indegree[MAX] = {0};

    for (int i=0; i<n; i++) {
        int nodeNum = sccLabel[i];
        for (int adjNode : adj[i]) {
            int nextNodeNum = sccLabel[adjNode];
            if (nodeNum == nextNodeNum) continue;
            graph[nodeNum].push_back(nextNodeNum); // nodeNum -> nextNodeNum
            indegree[nextNodeNum]++; // nextNodeNum의 indegree 증가
        }  
    }

    queue<int> q;
    for (int i=0; i<sccCnt; i++) if (indegree[i] == 0) {
        q.push(i);
        compIdx[i] = ++compNum; // indegree가 0인 노드는 SCC의 최상위 노드이므로, 최소 인원은 1명이다.
        minCompSize[compNum] = maxCompSize[compNum] = sccSize[i]; // SCC의 크기를 저장한다.
    }

    while (!q.empty()) {
        int curr = q.front(); q.pop();
        for (int nxt : graph[curr]) {
            compIdx[nxt] = compIdx[curr]; // nextNodeNum의 최소 인원은 currNodeNum의 최소 인원 + 1이다.
            maxCompSize[compIdx[nxt]] += sccSize[nxt]; // nextNodeNum의 최대 인원은 currNodeNum의 최대 인원 + nextNodeNum의 크기이다.

            if (--indegree[nxt] == 0) q.push(nxt);
        }
    }
}

int knapsack(int now, int value) {
    if (now > compNum) return 0; // 더 이상 노드가 없다면 종료한다.

    int& ret = cache[now][value];
    if (ret != -1) return ret;

    ret = knapsack(now+1, value); // now번째 노드를 데려가지 않는 경우
    if (value >= minCompSize[now]) {
        for (int i=minCompSize[now]; i<=maxCompSize[now]; i++) {
            if (i > value) break;
            ret = max(ret, knapsack(now+1, value-i) + i);
        }
    }

    return ret;
}