1. 문제 설명
1014번: 컨닝
최백준은 서강대학교에서 “컨닝의 기술”이라는 과목을 가르치고 있다. 이 과목은 상당히 까다롭기로 정평이 나있기 때문에, 몇몇 학생들은 시험을 보는 도중에 다른 사람의 답지를 베끼려 한
www.acmicpc.net
2. 아이디어
처음 보자마자 dynamic programing을 사용하면 풀 수 있을 것이라 생각하고 접근 중이었는데, 풀다가 심심해서 알고리즘 분류표를 봤더니 최대 유량이 태그에 있었다.
이 문제를 최대 유량으로 해결할 수 있다고..???
뒤져보니 컨닝 2는 dp와 비트마스킹으로 풀어야 시간복잡도 내에 해결 가능하지만, 컨닝 1은 최대 유량으로 해결 가능하다는 글을 보자마자 일단 dp 풀이는 미루고 최대유량으로 접근하는 방법을 찾아보았다.


하지만 도저히 해결 방법이 보이질 않아서 골똘히 생각해보니 이전에 최대 유량 문제들을 정확히 이해하지 않고 넘어갔었던 것 때문이라고 생각하여, 이번에는 아예 작정하고 Network Flow를 수학적으로 증명하였다.
다만, 이 포스팅에서는 증명을 다루지는 않을 것이다.
사실 이렇게 실컷 정리해놓고도 이 문제를 최대 유량하고 접목시킨다는 것이 매우매우 어려웠는데,
'쾨닉의 정리'를 이용하면 가능하다는 키워드만 잡고 다시 분석해본 결과 끝내 방법을 찾을 수 있었다.
분석은 가장 작은 단위를 놓고 일반화를 시킴으로써 문제를 해결하는 것이 편하다.
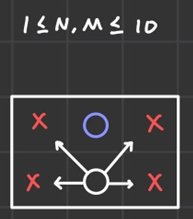
위의 경우에서 컨닝이 불가능한 자리는 흰색 정점 바로 앞의 파란색 정점밖에 없다.
하지만 2x3 크기의 자리에서 실제로 최대 인원을 배치할 수 있는 경우는 x표시가 된 자리에 4명의 인원을 배치하는 것이다.
모든 자리를 하나의 정점으로 취급하고 다시 그림을 그려보자.
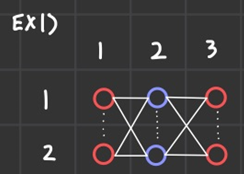
그래프는 다음과 같이 재구성될 수 있다.
간선은 컨닝이 현재 위치에서 컨닝이 가능한 자리로만 이어주면 되는 것이 물리적 이유이고,
이러한 특성 덕분에 논리적으로 이분 매칭 그래프를 얻을 수 있게된다.
이게 무슨 소린가?
각각의 노드에 번호를 매기고 자리를 조금 조작해주면 재밌는 결과를 얻을 수 있다.
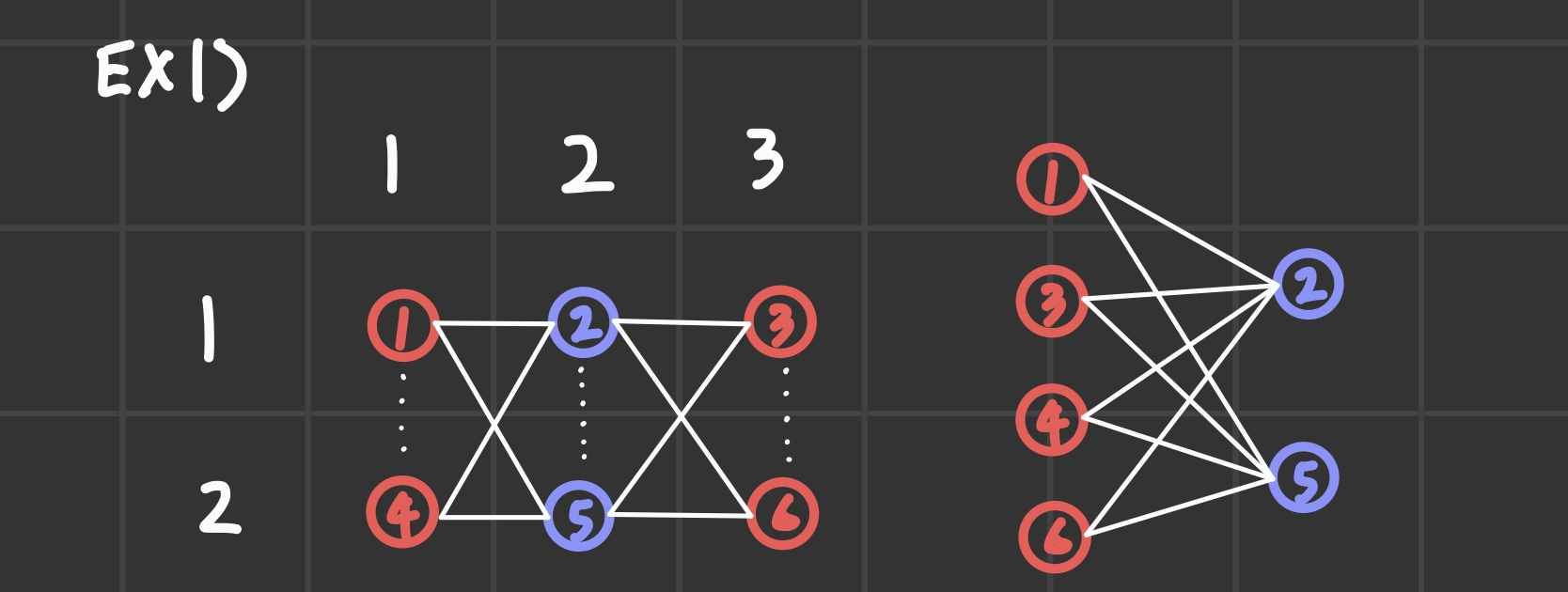
이제 우리가 흔히 아는 문제인 bipartite graph의 형태가 나옴을 알 수 있게 된다.
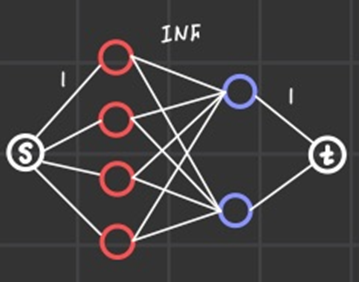
bipartite graph는 곧 source와 sink 노드를 연결함으로써 최대 유량문제로써 접근할 수 있게 되는 것이다.
여기까지는 기본적인 Network Flow에 대한 이해가 있다면 충분히 알 수 있는 내용이다.
하지만 궁극적인 의문이 하나 생긴다.
이걸 이용해서 어떻게 문제를 해결할 수 있다는 것인가?
쾨닉의 정리에 의하면, minimum vertext cover는 maximum matching의 개수와 같다.
일단 설명 전에 이 문제의 솔루션을 해결하는 과정을 정리하면 이렇다.
- vertex cover와 문제의 관련성 이해
- minimum vertex cover == maximum matching (König's theorem)
- bipartite graph에서 maximum matching == maximum flow
모든 내용을 설명할 수는 없으니 간단하게 중요한 내용만 짚고 가자.
1. vertex cover
임의의 그래프 G = (V, E)에 대해서 부분집합 U ≤ V에 대해서, 모든 간선의 한 끝 점이 U에 속하면 U를 vertex cover라 한다.
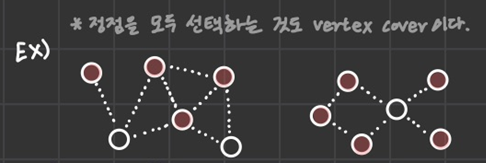
선택된 정점과 해당 정점에 연결된 간선을 모두 제거했을 때, graph 상에 간선이 하나도 존재하지 않는다면 vertex cover라고 할 수 있다.
이말은 즉슨 모든 정점을 선택해도 vertex cover가 가능하다는 뜻인데, 이 분야의 특징은 항상 최적화가 중요하다.
즉, maximum vertex cover가 궁금한 게 아니라 minimum vertex cover가 궁금하다는 뜻인데 첫 번째 그림의 경우엔 minimum vertex cover을 찾아보면 다음과 같다.
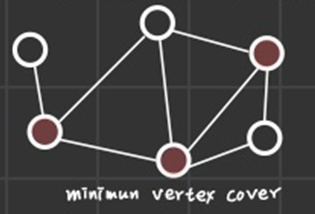
3개의 정점을 선택함으로써 연결된 간선을 모두 날려보면 graph 상에 존재하는 간선은 남지 않게 된다.
따라서 해당 정점의 선택의 집합은 minimum vertex cover라고 말할 수 있게 된다.
vertex cover에 대한 이해가 됐다면, 이 개념을 문제에 접목시켜보자.
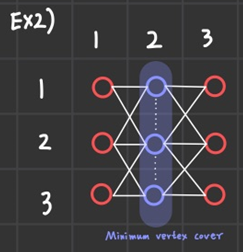
위와 같은 배치가 주어졌을 때, 사이에 3자리를 선택하면 minimum vertex cover가 된다.
그런데 생각해보면 전체 자리에서 minimum vertex cover를 날린다면?
그것이 바로 총 좌석에서 사람이 최대로 앉을 수 있는 자리가 된다.
만약 부서진 자리가 섞여있다면 얘기가 달라질 수도 있다고 생각할 수 있지만, 다른 예시를 하나 더 살펴보자.
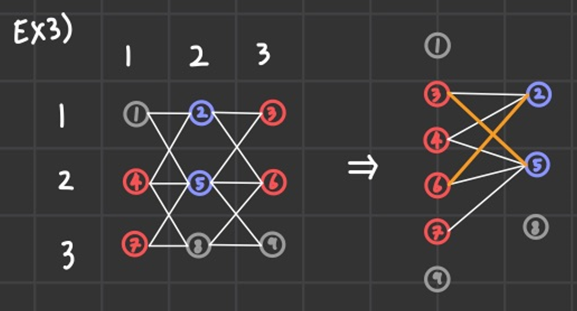
1, 8, 9번 자리가 부서진 경우에는 애초에 간선을 연결하지 않으면 된다.
의문이 든다면 몇 가지 테스트 케이스에 대해서 스스로 이해할 수 있도록 해보자.
자, 여기까지 왔다면 output의 값은 (전체 자리 수) - (부서진 자리 수) - (최소 버텍스 커버)임을 알 수 있다.
전체 자리 수도 알겠고, 부서진 자리 수는 그냥 cnt하면 된다지만 문제는 "최소 버텍스 커버를 어떻게 구하는가?"로 논점이 바뀌게 된다.
2. minimum vertex cover == maximum matching at bipartite graph (König's theorem)
쾨닉의 정리의 결론은 한 가지 의문으로부터 출발한다.
'과연 동일한 그래프에서 matching의 크기보다 작은 vertex cover를 찾을 수 있는가?'
이 의문에 대한 답은 "불가능하다"가 맞다.
matching에 속한 Edge들의 endpoint는 언제나 다르다.
즉, vertex cover의 정점 하나가 처리 가능한 matching의 간선은 최대 하나가 된다.

따라서 정의에 의해 bipartite graph에서 maximum matching의 개수와 minimum vertex cover의 개수는 같다.
(bipartite graph가 아니면 np-hard problem이 되기 때문에 다른 접근이 필요하다.)
최종적으로 정점에 대해 기준을 잡았다가 이를 간선에 대한 문제로 관점을 바꿀 수 있게 되었다.
이분 그래프에서 최대 매칭 문제로 바뀜으로써 이제 우리에게 매우 익숙한 형태로 코드를 작성할 수 있게 되었다.
바로 "Maximum Network Flow"이다.
3. maximum matching == maximum flow at bipartite graph
maximum flow를 이용하는 방법은 dfs를 이용하는 포드-풀커슨 알고리즘이나 bfs를 이용하는 애드몬드 카프 알고리즘을 사용하면 된다.
시간 복잡도 상으로 애드몬드 카프 알고리즘을 사용하는 것이 더 나을 수 있다고 생각할 수 있지만
이 문제는 모든 edge capacity가 1이기 때문에 Flow가 적고 Edge가 많은 경우 포드-풀커슨 알고리즘이 구현 측면으로나 활용도 측면으로나 훨씬 용이하게 풀릴 수 있다.
(애드몬드 카프 알고리즘을 쓰려면 source와 sink를 각 노드에 link 시키는 작업을 수반해야 하기 때문에 좀 귀찮아진다.)
지금까지 모든 내용을 순차적으로 통합했을 때, 작성해야 할 코드는 다음과 같다.
1. 모든 정점에 번호를 매겨준다. (구분을 위함)
2. 컨닝이 가능한 좌석에 대해 간선을 이어준다.
3. 완성된 정보를 토대로 포드-풀커슨 알고리즘을 이용해 max flow를 구해준다.
4. (전체 자리수) - (부서진 자리수) - (minimum vertex cover == max matching == max flow) 출력
일련의 과정대로 문제를 해결하면 바로 해결할 수 있다.
코드 작성 자체는 쉬운데 최대유량 개념과 접목하는 게 매우 힘든 문제였다.
하지만 덕분에 이전부터 이해 안 가던 Network Flow에 대한 개념을 확실하게 잡을 수 있었다.
3. 코드
#include <iostream>
#include <cstring>
#include <string>
#include <sstream>
#include <vector>
#include <tuple>
#define endl "\n"
using namespace std;
typedef tuple<int, int> tii;
char map[15][15];
int aMatch[50], bMatch[50];
bool visited[50];
vector<tii> vc = {{-1,-1}, {0,-1}, {1,-1}, {-1,1}, {0,1}, {1,1}};
bool dfs(int now, vector<int> adj[50]) {
if (visited[now]) return false;
visited[now] = true;
for (int nxt : adj[now]) {
if (bMatch[nxt] == -1 || dfs(bMatch[nxt], adj)) {
aMatch[now] = nxt;
bMatch[nxt] = now;
return true;
}
}
return false;
}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int c; cin >> c;
while (c--) {
int n, m; cin >> n >> m;
for (int i=0; i<n; i++) cin >> map[i];
int nodeNum[10][10];
int A, B; A = B = 0;
int broken = 0;
for (int i=0; i<n; i++) for (int j=0; j<m; j++) {
if (map[i][j] == 'x') broken++;
nodeNum[i][j] = (j % 2 == 0) ? A++ : B++;
}
vector<int> adj[50];
for (int i=0; i<n; i++) for (int j=0; j<m; j+=2) {
if (map[i][j] == 'x') continue;
for (tii t : vc) {
int ny = i + get<0>(t); int nx = j + get<1>(t);
if (0 <= ny && ny < n && 0 <= nx && nx < m && map[ny][nx] != 'x')
adj[nodeNum[i][j]].push_back(nodeNum[ny][nx]);
}
}
int maxMatch = 0;
memset(aMatch, -1, sizeof(aMatch));
memset(bMatch, -1, sizeof(bMatch));
for (int i=0; i<A; i++) {
memset(visited, 0, sizeof(visited));
if (dfs(i, adj)) maxMatch++;
}
cout << n*m - broken - maxMatch << endl;
}
return 0;
}