[Python] 2042 - 구간 합 구하기 (골드1)

1. 문제 설명

https://www.acmicpc.net/problem/2042

2042번: 구간 합 구하기

 

---

2. 아이디어

sum() 함수를 사용해서 풀겠다는 얄팍한 생각으로는 찢을 수 없는 문제다.

시간복잡도 \(O(N)\)이 걸리는데 최악의 케이스 N*K (1,000,000 * 10,000)만 고려해주어도

벌써 백억이 넘어가니 2초 내에 해결할 수 없다.

 

이걸 해결할 만한 방법은 어딘가 구간합을 계속 '저장'하고 '업데이트'시켜주어야만 한다는 뜻이다.

값을 기억한다는 점에서 DP를 떠올려볼 수도 있겠지만, 업데이트 과정이 너무 느리다.

그렇다면 결국 쓸만한 건 Segment Tree밖에 남지 않는다.

라는 식으로 추론하는 척 했지만 구간 합 구하기 문제에서 세그먼트 트리를 쓰는 건 사실 유명하다.

 

가장 아래쪽에 있는 노드에 input값을 넣어주고 두 개씩 합을 구하며 거슬러 올라오면 된다.

처음 세그먼트 트리 상태

구간합을 구한 후의 세그먼트 트리

3~6까지 구간합을 구해올 때

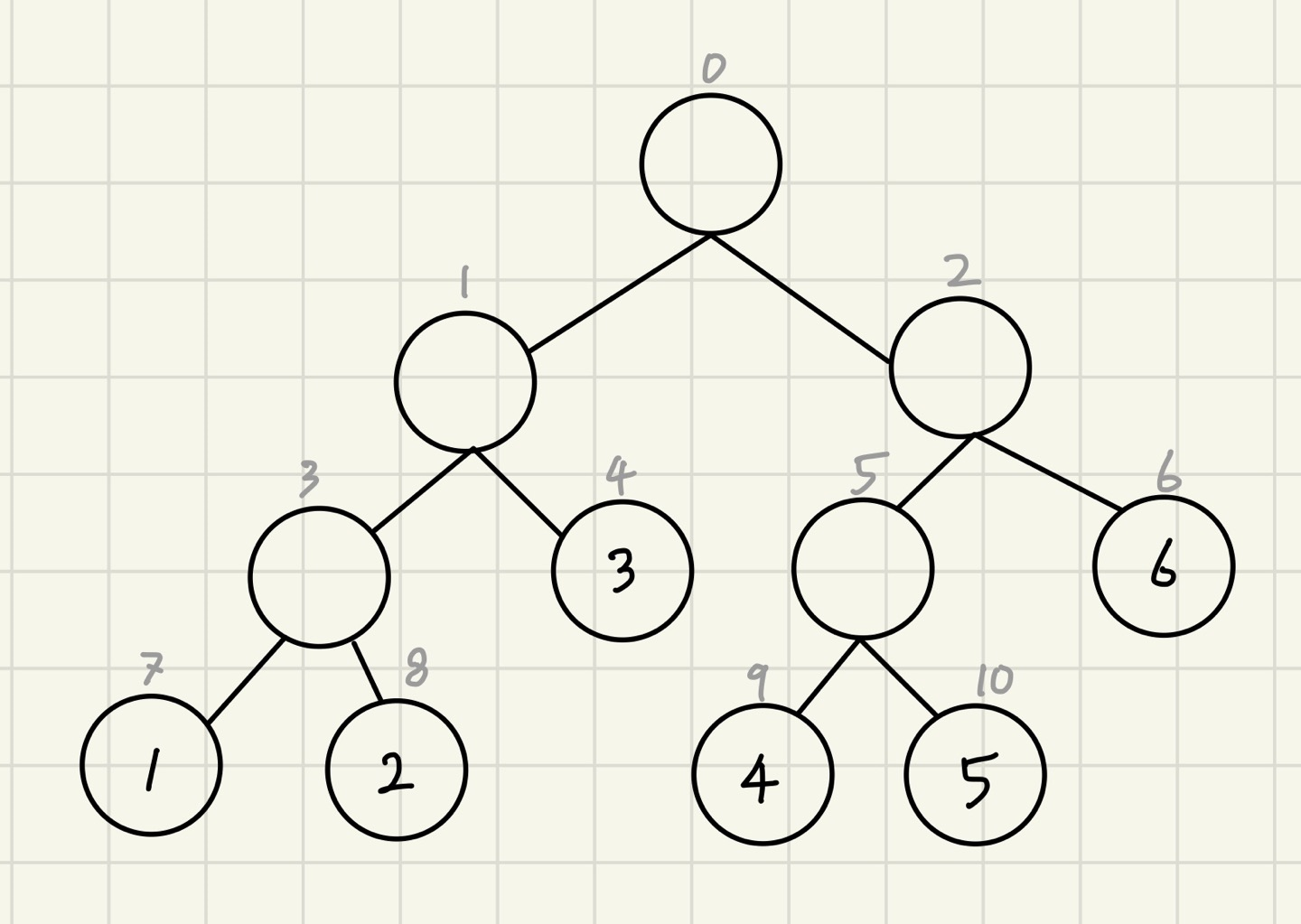
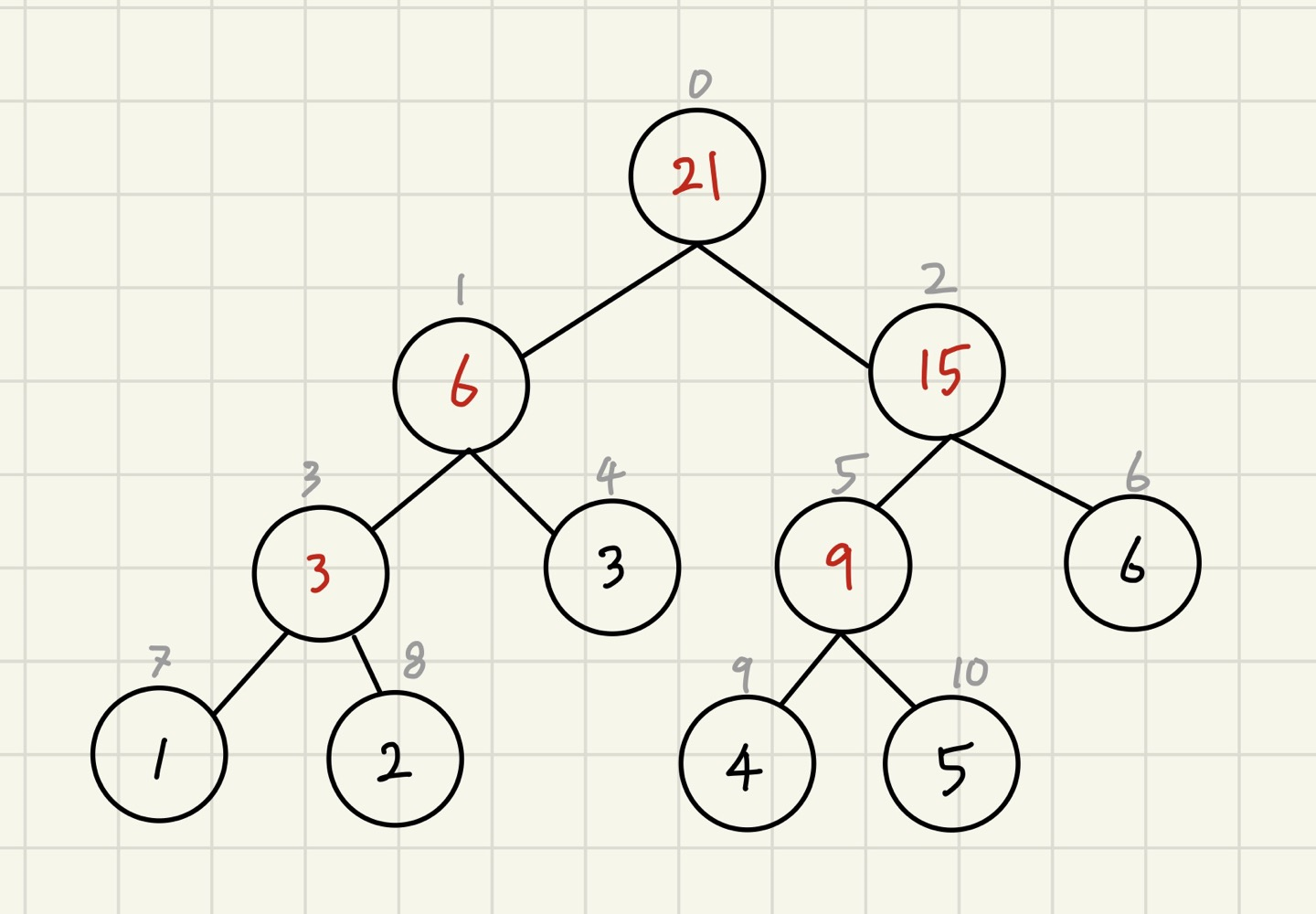
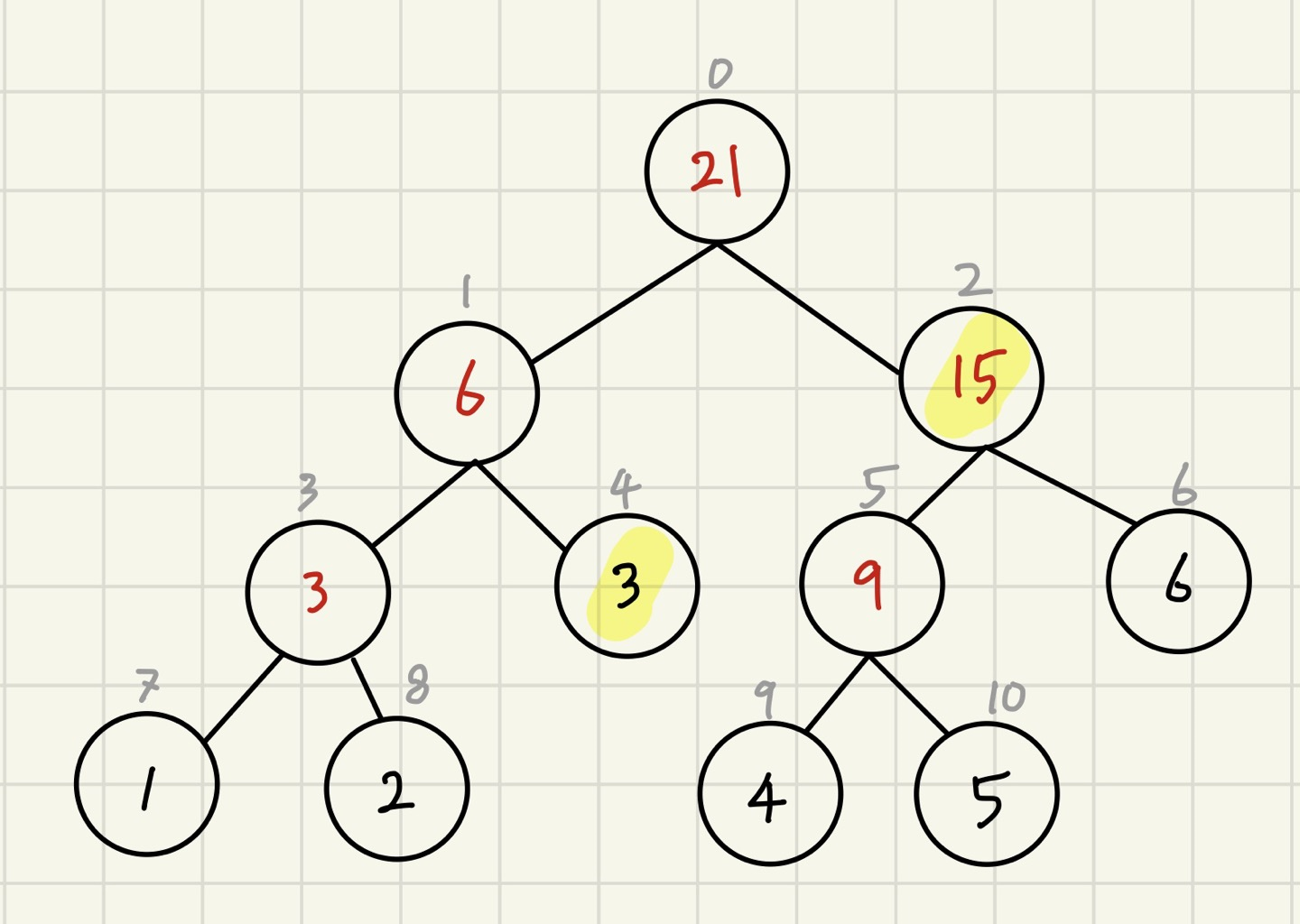
업데이트 하는 과정은 해당 위치까지 들어가서 값을 바꾼 후 올라오면서 구간합을 업데이트 해주면 된다.

이렇게 하면 구간합은 언제나 logN 이므로 시간초과에서 벗어날 수 있다.

 

---

3. 코드

import sys

input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)

n, m, k = map(int, input().split())
arr = [int(input()) for _ in range(n)]

def calc_size_tree(n):
    tmp = 1
    while tmp < n:
        tmp <<= 1
    tmp <<= 1

    return tmp

def create_tree(left, right, idx, seg_tree):
    if left == right:
        seg_tree[idx] = arr[left]
        return seg_tree[idx]

    mid = (left + right) // 2
    seg_tree[idx] = create_tree(left, mid, idx*2+1, seg_tree) + create_tree(mid+1, right, idx*2+2, seg_tree)
    return seg_tree[idx]

def update_tree(left, right, idx, b, c, seg_tree):
    if b < left or right < b:
        return
    
    seg_tree[idx] += c

    if left == right:
        return

    mid = (left + right) // 2
    update_tree(left, mid, idx*2+1, b, c, seg_tree)
    update_tree(mid+1, right, idx*2+2, b, c, seg_tree)

def calc_sum(left, right, idx, b, c, seg_tree):
    if left > c or right < b:
        return 0
    
    if b <= left and right <= c:
        return seg_tree[idx]

    mid = (left + right) // 2
    return calc_sum(left, mid, idx*2+1, b, c, seg_tree) + calc_sum(mid+1, right, idx*2+2, b, c, seg_tree)

def solution():
    seg_tree = [0] * calc_size_tree(n)
    create_tree(0, len(arr)-1, 0, seg_tree)

    for _ in range(m+k):
        a, b, c = map(int, input().split())
        if a == 1:
            update_tree(0, n-1, 0, b-1, c - arr[b-1], seg_tree)
            arr[b-1] = c
        else:
            print(calc_sum(0, n-1, 0, b-1, c-1, seg_tree))

solution()