[C++] 1067 - 이동 (플래티넘1) : FFT(고속 푸리에 변환)
1. 문제 설명
1067번: 이동
N개의 수가 있는 X와 Y가 있다. 이때 X나 Y를 순환 이동시킬 수 있다. 순환 이동이란 마지막 원소를 제거하고 그 수를 맨 앞으로 다시 삽입하는 것을 말한다. 예를 들어, {1, 2, 3}을 순환 이동시키면
www.acmicpc.net
컴공 복전 2학년 수업으로 데이터 통신을 듣다가 교수님께서 FFT라는 알고리즘을 언급하셨는데, 너무 어려운 내용이라 보통 석사 과정에서 배우는 내용이라 로직을 알 필요는 없다고 하셨다.
하지만...'내가 모르는 알고리즘?'이라는 생각이 뇌리에 꽂히면서 이 로직과 원리를 분석하는데 무려 3일이란 시간이 소모됐다. (교수님께서 하지 말라는 데는 다 이유가 있다.)
지금도 증명 단계에서 정확이 알고 있다고 할 수는 없다. 이산 수학을 공부한 적도 없는데 이산 수학적 관점으로 문제에 접근한다는 게 너무 어렵다.
로직 자체는 자명한 증명들을 기반으로 읽히면 그래도 이해할 수 있다.
참조한 블로그는 너무 많은 관계로 글 중간중간 주소를 붙여놓을 생각.
[Math Proof] Fourier Series
어느정도 이해했다고 생각했는데 더닝-크루거 효과대로 멍청함의 피크를 찍고 절망의 늪에서 허우적 거리는 중이다. 그래도 지금까지 공부한 부분이라도 포스팅 해야지. 수학적 증명과 물리적
jaeseo0519.tistory.com
푸리에 분석에 대한 수학적을 대해 정리해두었다.
아직 Fourier Transform까지는 도달하지 못 했지만, 종강하고 나면 다시 해볼 생각.
2. 아이디어



틀린 내용이 무조건 있을 것이다. 혹시 발견하신 분이 계시다면 댓글로 지적부탁드립니다.
이 문제는 Discrete Fourier Transform에 대해서만 이해하면 끝나는 줄 알고 열심히 팼는데, convolution이라는 수문장이 퇴로를 가로막아서 앞 뒤로 막힌 채 진짜 죽기 직전까지 맞았다.
수학 공식한테 얻어 맞았다는 표현만큼 적절한 표현이 없다. 복싱하다가도 눈 앞에 주파수 도메인이 아른거렸다..
우선 굳이 시간 도메인을 생각하지 않아도 길이가 N개인 2개의 수열에 대해 순환곱을 하는 것은 단순하게 O(N^2)의 방법이 가장 먼저 떠오를 것이다.
하지만 N의 최대가 60,000이므로 O(N^2)의 시간복잡도를 가지고는 해결할 수 없다.
따라서 "순환한다"라는 개념을 적용시키기 위해 시간 도메인의 영역으로 문제를 끌고와서 주파수 도메인으로 치환시킨 후에 합성곱을 하여 다시 시간 도메인으로 치환하면 최댓값이 나온다.
ㅋㅋ 골 때리네.
1. FFT & IFFT
우선, 시간 도메인과 주파수 도메인으로 왔다갔다 하게 치환시켜주는 게 DFT, IDFT고 이걸 더 빠른 속도로 개선시킨 것이 FFT, IFFT 알고리즘이다.
순환하면서 곱한다는 개념은 이산 수학의 convolution의 개념을 이해하면 편한데, 난 몰라서 수학적 공식을 머리에 때려놓고 증명(당)했다.
로직은 수학적 증명 이해하면 생각보다 쉽게 해결된다.

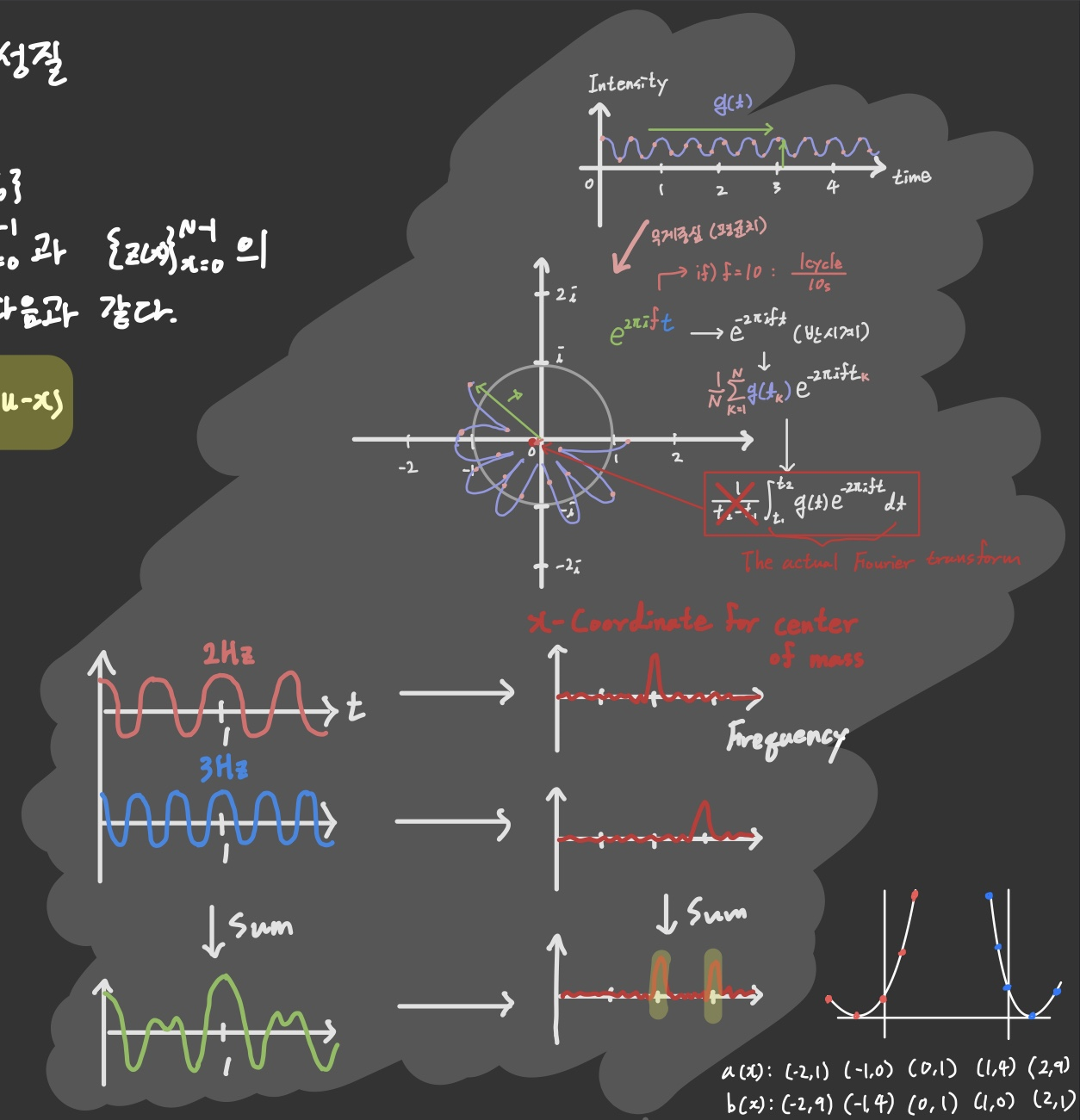
주전공이 화학공학인지라 오일러 공식에 대해 이미 공부해둬서 이 부분은 바로 이해할 수 있었다.
복소수 좌표를 한 바퀴 회전하는데 1초라 가정하면 N이 16일 땐 16Hz가 된다.
그러면 sampling된 그래프가 질량을 가진다고 가정하고 복소수 좌표를 감싸듯이 그리면 무게 중심의 이동을 알 수 있다.
* 모바일 화면에선 수식이 html 형식으로 보여서 불편하실 수 있습니다..
Foward Discrete Fourier Transform(DFT)
Inverse Discrete Fourier Transform(IDFT)
이걸 좀 더 빠르게 할 수 있는 방법이 뭔지 연구하다가 홀수항과 짝수항에 대해 분할하여 연산하고 merge하면 값을 구할 수 있다.
DFT to FFT

과연 그럴까? 그렇다면 직접 해보면 된다.
FFT의 대표적인 알고리즘은 Cooley-Tukey Alogorithm을 사용하는데 이 알고리즘은 N이 2의 거듭제곱인 경우에 사용될 수 있기 때문에 우선 배열이 2의 거듭제곱 크기만큼 있다고 치자.
N = 8이라고 가정하고 우선 수학 공식에 대입해보자.

보시다시피 F(u)를 구하기 위해 잘게 쪼개다 보면 결국 기저 사례를 만들기 위해 f(u)를 어떻게 sort해야 할지 알 수 있게 된다.

f항들을 순서대로 sort하여 merge하며 거슬러 올라가면 최종적으로 F(u)를 구할 수 있게 된다!
진짜 놀랍지 않은가?? 처음에 이거 보고 감탄했었는데 (여기서 관뒀어야 했다.)
그럼 여기서 f항을 어떤 기준으로 sort할 것이냐가 관건인데, 자세한 내용은 아래 블로그를 참조하자.
Fast Fourier Transform
고속 푸리에 변환(Fast Fourier Transform, FFT)은 convolution을 $O(N\log N)$에 구할 때 활용된다. 이 포스트에서는 코드 자체보다도 FFT 알고리즘의 원리를 알아보는 것이 목적이다. 코드만 보고싶다면 맨 아
tistory.joonhyung.xyz
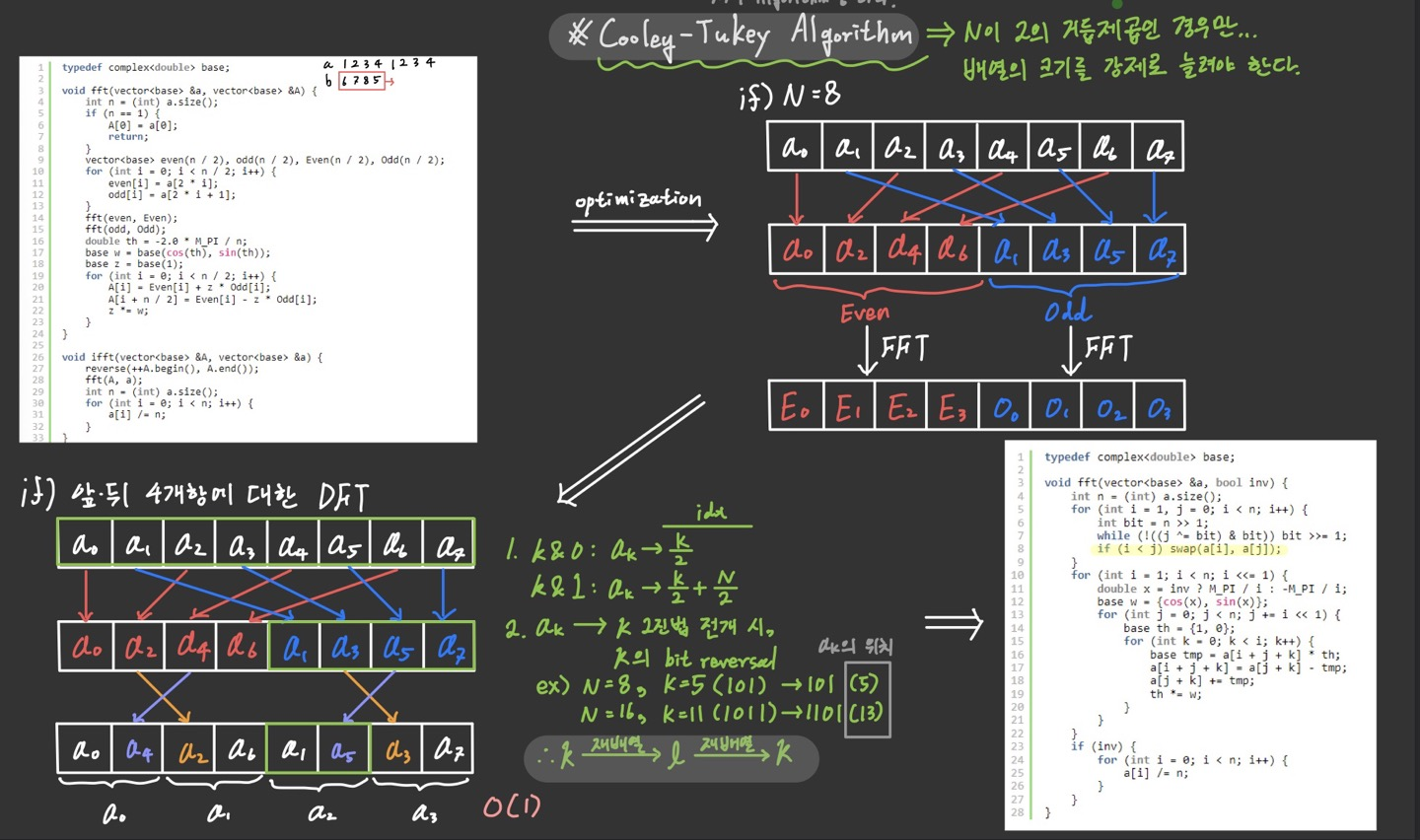
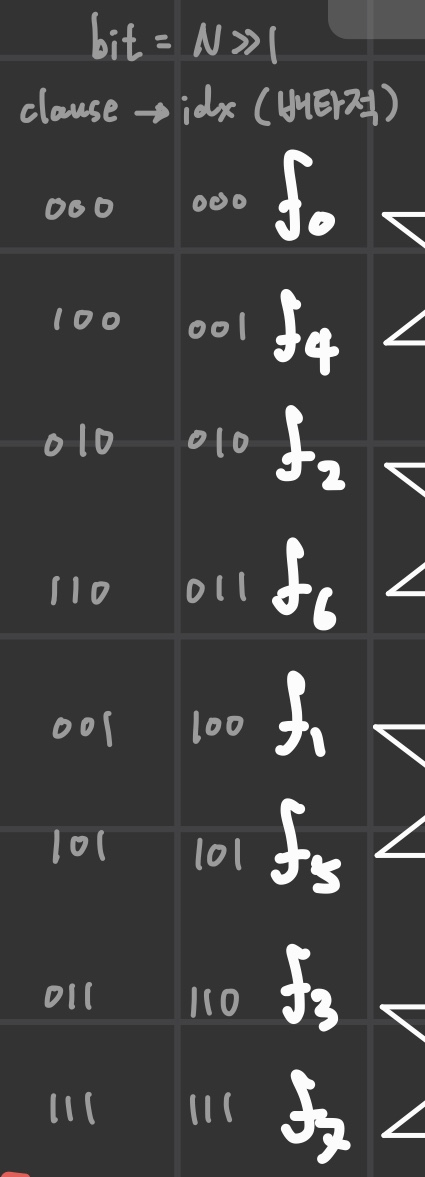
이 글을 요약하면 이렇게 된다.
f(k)항의 k를 2진법 전개해보면 비트를 대칭적으로 역전시켰을 때, 최종 배치가 된다.
이 부분은 이론은 알겠는데, 아직 로직이 어떻게 이걸 해내는지 파악하지 못 해서 분석 중이다.
어쨌든 주파수 도메인을 다시 시간 도메인으로 바꾸는 것이 IFFT 알고리즘인데 위에서 IDFT 공식을 보면 쉽게 해결된다.
이게 결국 지수 영역에서 돌아가고 있는 거니까 역으로 돌리면서 N으로 나누어주면 해결된다.
이렇게 하면 두 개의 수열에 대한 주파수 도메인을 구한 셈인데, 이걸 convolution을 하면 순환이동이 된단다.
ㅋㅋ 이건 또 뭔 소리야.
2. Convolution
[ Math ] Convolution(합성곱)의 원리와 목적
[ Math ] Convolution(합성곱)의 원리와 목적 Convolution Convolution (합성곱) 많이들 들어 보셨을 겁니다. 의미적으로는 두 함수를 서로 곱해서 합한다는 것이지요. 합성곱을 공부하셨다면 아래의 질문
supermemi.tistory.com
여기서 한참을 해맸는데, 진짜 도움이 많이 되었다.
일단 결론부터 말하자면 이 문제는 수열 하나를 2배로 늘리고, 다른 하나는 역순으로 정렬하여 순환곱을 해야한다.
여기서 진짜 뭔 소린지 알 수가 없었는데, convolution의 공식을 살펴보면 이해할 수 있다. (머리는 모르겠는데, 가슴으로는 이해하게 된다.)
백준 #1067 이동(FFT)
이번 문제는 Platinum II 난이도 문제입니다. 이 문제를 풀기 위해서는 길쌈 코드(Convolution Code)에 대한 이해가 필요합니다. 길쌈 코드는 크게 순환하지 않는 코드와 순환하는 코드가 있습니다. 이
sdev.tistory.com
유투브 영상을 시청해보면 아날로그 시그널을 sampling하는 단계에서 이 내용이 나온다.

결론만 말하자면 두 연속함수 f,g를 convolution하면 다음 공식을 따른다.
물론 여긴 discrete function이므로 적분이 아닌 단순 합으로 표현한다.
어쨌든 convolution을 위해서 두 함수 중 하나를 반전시킨 함수 g(τ-t)를 복소수 좌표에 대해서 전이(shift)하며, 두 함수를 곱하여 기록하면 τ 변화에 대한 기록이 곧 convolution이 된다.
이 과정에서 두 함수가 겹치거나, 0이 나올 수도 있다.
사실 더 자세히 설명하려면 행렬 개념까지 끌고 와야하는데 이미 이 문제에 시간을 너무 쏟아부어서, 이이상 붙잡고 있을 수가 없어서 일단 로직만 이해하고 증명 단계를 다소 많이 패스해버렸다.
머리가 좀만 더 좋았어도 더 많은 걸 이해할 수 있었을텐데, 그 부분이 너무 아쉽긴 하지만 교수님께 이론을 여쭤봐도 되려나 ㅎㅎ. 대학원 끌려가려나. 무서워서 여쭤보지 못 하겠다.
3. 코드
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <complex>
#define endl "\n"
#define ll long long
using namespace std;
typedef complex<double> base;
const double PI = acos(-1);
void fft(vector<base> &a, bool inv) {
int n = (int)a.size();
for (int i = 1, j = 0; i < n; i++) { // clause f sort (정확한 원리는 아직 이해 X)
for (int bit = n >> 1; !((j^=bit)&bit); bit >>=1) // f_odd항과 f_even 분리
if (i < j) swap(a[i], a[j]);
}
for (int i=1; i<n; i<<=1) {
double angle = (inv ? -1 : 1) * PI / i; // inv ? IFFT : FFT
base w = {cos(angle), sin(angle)}; // 감는 각도
for (int j=0; j<n; j += i << 1) {
base th = {1, 0};
for (int k=0; k < i; k++) {
base tmp = a[i+j+k] * th; // wH(u)
a[i+j+k] = a[j+k] - tmp; // F(u) = G(u) - wH(u)
a[j+k] += tmp; // F(u) = G(u) + wH(u)
th *= w; // 복소수 그래프 상에서 회전
}
}
}
if (inv) // IFFT (수학적으로 증명됨.)
for (int i=0; i<n; i++)
a[i] /= n;
}
vector<ll> multiply(vector<ll> &a, vector<ll> &b) {
vector<base> A(a.begin(), a.end()), B(b.begin(), b.end());
int n = 1; // 2의 거듭제곱 자릿수로 resize
while (n < A.size() + B.size()) n <<= 1; // (n < A.size() || n < B.size()) => 오답. why?
// FFT
A.resize(n); fft(A, false);
B.resize(n); fft(B, false);
for (int i=0; i<n; i++) A[i] *= B[i];
fft(A, true); // IFFT
vector<ll> res(n);
for(int i=0; i<n; i++) res[i] = (ll)round(A[i].real()); // 실수부
return res;
}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin >> n;
vector<ll> a(n*2), b(n);
for (int i=0; i<n; i++) {
cin >> a[i];
a[i + n] = a[i];
}
for (int i=1; i <= n; i++) cin >> b[n - i];
vector<ll> res = multiply(a, b);
ll answer = 0;
for (ll v : res) answer = max(answer, v);
cout << answer << endl;
return 0;
}