[C++] 12736 - Fireworks (다이아몬드1)

1. 문제 설명

 

12736번: Fireworks

다이아쯤 가면 어떤 문제를 풀까 궁금해서 접근했다가 죽는 줄 알았다.

구현 + 수학 + 알고리즘을 모두 합친 문제라고 해야하나..

심지어 APIO 2016 킬러 문제인 줄 알았으면 호기심도 안 가졌을 것. 🙄

문제를 풀었다기 보다는 공부나 연구했다가 더 맞는 말이므로 코드는 따로 올리지 않겠다.

어찌저찌 구현은 했지만 핵심 코드는 다른 분들의 코드를 분석하면서 참조(암기)해버렸기 때문에, 나중에 이 문제가 잊혀질 때쯤 다시 풀게 된다면 그때 코드를 올릴 예정이다.

"이건 표절 아니냐?"라고 해도 할 말이 없다. 아까도 언급했다시피 핵심적인 코드는 분석 과정에서 거의 외워버리는 바람에 최대한 나만의 노력으로 하려고 했어도 반영이 되지 않았을리가 없기 때문.

그렇다고 푼 게 통과되는지 확인도 못 해보고 블로그에 정리할 수는 없으니 제출했을 뿐.

의미도 없는 레벨 따위를 채워보겠다고 제출한 심산은 아니었다.

---

2. 아이디어

 

절대!! 내 아이디어가 아니다.

아래 블로그에서 엄청 큰 도움을 받았다.

APIO 2016

 

문제의 개요는 다음과 같다.

처음 신관에 연결되어 있는 폭죽의 정보가 주어졌을 때,

이 폭죽을 한 번에 터뜨리고 싶다면 도화선 길이를 최소로 조정하는 값을 계산해야 한다.

 

당연히 트리를 이용해야 한다는 것은 알 수 있었고, 경우의 수를 따지기 위해서는 dynamic programming 또한 포함되어야 할 것이다.

Top-down으로 내려가기엔 정보가 부족하니까, 폭죽 정보를 담으면서 Bottom-up 방식으로 Edge를 타고 올라와야 한다.

시간복잡도를 고려했을 때, \(O((N+M)^{2})\)만큼의 시간이 걸리면 부분 점수 20점 정도밖에 얻질 못 한다.

보통 이런 경우에는 시간 복잡도를 log로 줄여야만 함을 의미한다.

 

문제는 여기서 dp를 어떻게 관리할 것이냐가 된다.

이전까지 다루던 dp는 경우의 수 정도로 취급했지, 이 경우엔 어떻게 접근할지 조차 막막했었다.

그런데 dp를 함수처럼 다루는 것을 보고 대체 무슨 소린가 싶어서 직접 함수를 그려보자 길이 보였다.

차근차근 해보자.

 

노드 u에 대하여 u의 서브트리에 존재하는 하위 노드들의 가중치를 변경하는 최소 비용을 나타내는 함수 f(t)를 정의한다.

함수 f(t)가 바로 dp이다. f(t)는 각 노드마다 모두 존재하고 경우의 수를 기록한다.

i번 연결점에 이어진 폭약들을 t시간에 터뜨리기 위한 최소비용이라고 이해하면 된다.

 

f(t) (== dp[t]) = v : 루트에서 v의 sub tree의 모든 노드까지의 거리를 x로 만들고자 할 때 드는 비용

leaf node의 경우에는 dp는 v일 때 0이고, 아닐 때는 무한대로 향하는 양상을 띤다.

internal node는 자식 노드들의 dp 배열의 합이되는데 \(C_{i}\)의 가중치를 지니는 Edge를 타고 올라오기 때문에 이를 고려해주어야 한다.

 

그래프를 좀 이상하게 그렸는데 직접 해보는 게 좋다.

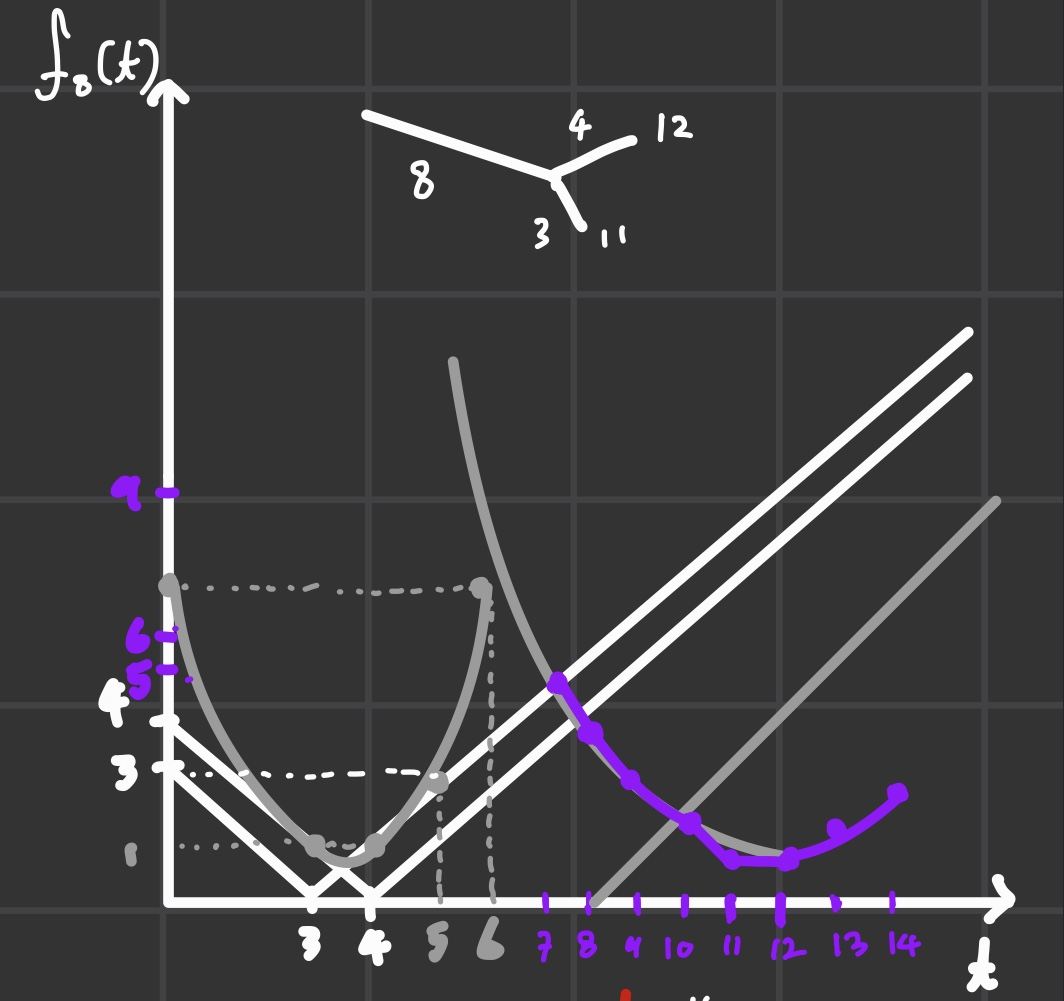
만약, 위의 이미지같은 Sub tree라면 그래프가 우측 그래프처럼 양상이 변하게 된다.

여기가 되게 중요한 포인트인데 자식 노드는 aT + b꼴의 값을 가진다. (T는 기울기 변화가 가장 큰 지점)

t가 증가할 때 부모 노드가 1만큼 증가한다는 것을 기억하자.

즉, 자식노드 i는 a=1, b=\(-c_{i}\)의 값을 가지고, 변곡점의 t는 { \(c_{i}\), \(c_{i}\) }가 된다.. (기울기가 -1에서 0으로 변하는 지점과 0에서 1로 변하는 지점)

게다가 dp 배열이 아래로 볼록한 함수 형태를 지닌다는 것을 알 수 있다.

하지만 여기서 함수를 다 더하면서 올라오는 과정은 필연적으로 \(O((N+M)^{2})\)만큼의 시간이 소요되므로 dp 관리를 더 효율적으로 처리해야만 한다.

 

그래프를 그리다 보면 한 가지 알 수 있는 점이 또 있는데, 바로 기울기가 변하는 점은 모두 정수 좌표이며 범위는 ±(sub tree의 leaf 개수)가 된다.

여기까지 이해하면 알겠지만, 이 문제는 dp 배열을 만들어서 처리하는 문제가 아니라 기울기가 +1 증가하는 변곡점을 저장해야만 한다.

기울기 변화가 1보다 큰 변곡점은 모두 의미가 없다.

변곡점 slope1, slope2를 찾았다면 부모 노드의 Edge비용만큼 오른쪽으로 이동해야 한다.

 

위의 내용들을 고려하면 이제 처리해야할 연산들이 정리된다.

1. priority_queue에 기울기가 +1씩 변하는 변곡점 좌표를 삽입한다. 만약 Leaf node라면 {\(c_{i}, c_{i}\)}가 된다.
2. Edge를 타고 올라오면서 기울기가 1보다 큰 부분을 pop해준다. -1의 경우에는 기울기가 0인 지점을 적절히 활용하자.
3. 두 개의 원소를 빼고 t축으로 Edge 비용인 \(c_{i}\)만큼 더하고 다시 저장한다.
4. 함수를 더할 때, 아직 부모 노드가 갱신되지 않았으면 그대로 복사하고, 아니라면 그냥 우선 순위 큐의 원소를 차례로 넣어주면 된다. (이 과정이 어려웠는데 HLD를 다시 공부해서 돌아오니까 겨우 구현에 성공했다.)

 

Dispatching (APIO 2012)

priority_queue를 합치는 과정은 위의 포스팅을 참조했다.

\(f_{i}(t)\)를 구성하는 큐의 원소 개수는 i번 연결점에 연결된 폭약 수에 비례하는 양상임을 알 수 있다.

함수를 합칠 때마다 우선 순위 큐의 사이즈가 2배 이상으로 증가하므로 이동 횟수가 O(log n)이고,

실제 이동할 때도 O(log n)만큼 소모되므로 같은 풀이 방법으로 접근한다면 이 문제의 최종 시간 복잡도는

\(O(N+M)log^{2}(N+M)\)이 된다.

 

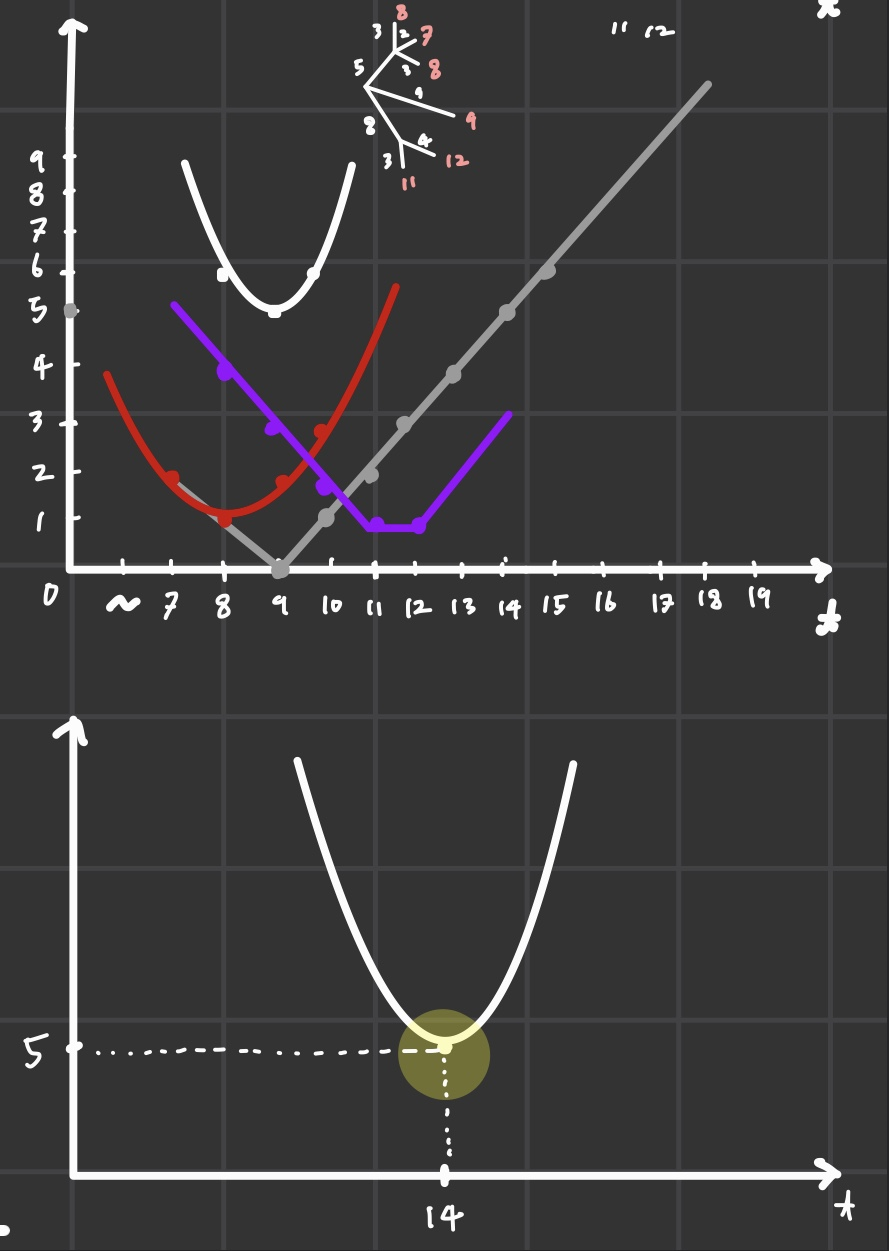
나처럼 DP를 함수로써 다루는 기술을 몰랐던 사람이라면 꼭 직접 그려봤으면 좋겠다.

막상 해보면 문제에 대한 이해도가 엄청 늘어나는 것을 느낄 수 있다.

 

아, 물론 그래프는 내 이해를 위해 그렸을 뿐 최종적으로 문제 풀이를 위한 코드와는 조금 다른 로직으로 흘러갔다. 아마도 이건 실력탓인 거 같다.